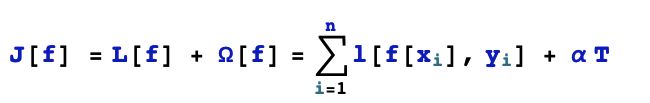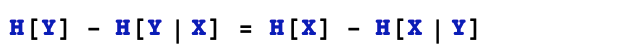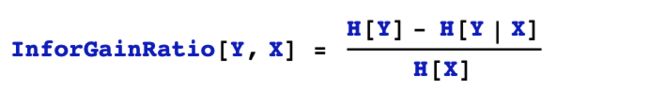30分钟理解决策树的基本原理
![]()
文章发布于公号【数智物语】 (ID:decision_engine),关注公号不错过每一篇干货。
来源 | Python与算法之美(ID:Python_Ai_Road)
作者 | 梁云1991
决策树是一种非参数的监督学习方法,它主要用于分类和回归问题。
决策树模型通过一系列if then决策规则的集合,将特征空间划分成有限个不相交的子区域,对于落在相同子区域的样本,决策树模型给出相同的预测值。
这些if then决策规则之间的层次关系形成一个树形结构,称之为决策树,这些不相交的子区域和树结构的叶子节点一一对应。
01
一,决策树原理概述
01
假设空间
下面从假设空间,目标函数,优化算法3方面阐述决策树算法的基本原理。
假设空间即我们对模型形式的先验假设,最终我们求得的模型必定符合我们对模型形式的先验假设。
决策树模型的先验形式可以表述成如下:
其中q[x]是从特征空间映射到节点编号空间的函数。决策树模型的关键是将特征空间划分成不相交的子区域,落在相同子区域的样本具有相同的预测值。
为了确定一棵决策树的完备结构,要明确如下两个方面:一是如何划分子区域,二是子区域的预测值取多少。
02
目标函数
目标函数即我们用什么标准来评价一个模型的好坏。目标函数决定了我们从假设空间中选择模型的偏好。
决策树的目标函数可以用来评价一棵决策树的好坏。这个目标函数应当包括两个方面的内容。第一个是反应决策树对样本数据点拟合准确度的损失项,第二个是反应决策树模型复杂程度的正则化项。
正则化项可以取模型的叶子节点的数量。即决策树模型划分得到的不相交子区域越多,我们认为模型越复杂。
对于损失项,如果是回归问题,损失项可以取平方损失,如果是分类问题,我们可以用不纯度来作为衡量标准。
为什么用不纯度呢?由于决策树的同一叶子节点上的所有样本都取相同的预测值,如果这些样本的真实 label 只有一种取值,那么这个叶子节点上的样本是非常“纯净”的,我们可以直接指定预测值为这个叶子节点上 label 的取值,预测误差为0。反之,如果叶子节点上不同样本的 label 的取值很杂乱,所谓众口难调,那么无论我们如何指定叶子节点上的预测值,总会有较大的预测误差。
那么,如何来衡量不纯度呢?一般有3种方法,信息熵,基尼不纯度,以及分类误差率。分类误差率即以 label 取值最多的那个类别作为叶子节点预测值时的误差率。信息熵和基尼不纯度我们稍后介绍。
03
优化算法
优化算法指的是通过什么样的方式调整我们的模型结构或模型超参数取值,使得模型的目标函数取值不断降低。
优化算法决定了我们用什么样的步骤在假设空间中寻找合适的模型。
对于决策树而言,优化算法包括树的生成策略和树的剪枝策略。
树的生成策略一般采用贪心的思想不断选择特征对特征空间进行切分。
树的剪枝策略一般分为预剪枝和后剪枝策略。一般来说后剪枝策略生成的决策树效果较好,但其计算成本也更高。
02
二,ID3,C4.5,CART决策树的对比
01
适用问题范围的不同
ID3算法只能处理离散特征的分类问题,C4.5能够处理离散特征和连续特征的分类问题,CART算法可以处理离散和连续特征的分类与回归问题。
02
假设空间的不同
ID3和C4.5算法使用的决策树可以是多分叉的,而CART算法的决策树必须是二叉树。
03
目标函数的不同
同样是处理分类问题时,在决定选择哪个特征进行决策树的分裂时,3个模型使用不同的判断标准。ID3算法以信息增益作为标准,C4.5算法以信息增益率作为标准,而CART算法以基尼不纯度增益作为标准。
04
优化算法的不同
3种算法有不同的剪枝策略。
ID3算法实际上没有剪枝策略,当叶子节点上的样本都属于同一个类别或者所有特征都使用过了的情况下决策树停止生长。
C4.5算法使用预剪枝策略,当分裂后的增益小于给定阈值或者叶子上的样本数量小于某个阈值或者叶子节点数量达到限定值或者树的深度达到限定值,决策树停止生长。
CART决策树主要使用后剪枝策略。
05
效果上的差异
ID3决策树是最早出现的决策树,C4.5是在它基础上的改进,CART决策树是更晚出现的,效果上一般而言CART树会好于C4.5,C4.5会好于ID3.
03
三,熵,条件熵,信息增益,信息增益率
01
熵
熵是对某个离散随机变量不确定性大小的一种度量。既然是反应不确定性的,我们的先验知识是当随机变量只有一种取值时,熵为0,当随机变量的取值可能性越多,在各个可能性之间的概率分布越平均,熵越大。熵的计算公式满足这些先验的特性。注意,熵只能度量离散随机变量的不确定性。
在决策树的应用场景中,我们实际上是用经验熵来衡量标签取值分布的“纯度”的,即用频率分布代替概率分布进行计算。
02
条件熵
所谓条件熵,是指给定随机变量X的取值的前提下,随机事件Y的不确定性的一种度量。
在决策树的应用场景中,条件熵的含义更加清晰明了,即按照离散特征X的取值将样本空间划分成多个叶子节点,各个叶子节点上样本标签Y取值的熵不纯度的加权平均。
03
信息增益
随机变量X对于随机变量Y的信息增益被定义成Y的熵和Y对X的条件熵之差。
在决策树的应用场景中,信息增益的含义就是特征X对样本标签Y不确定性减少的贡献。
信息增益也叫做互信息。互信息存在如下特性,Y对X的互信息和X对Y的互信息是相等的。互信息是衡量两个离散随机变量之前相关性的一种常用指标。
简单证明如下:
04
信息增益率
ID3模型采用信息增益作为待分裂特征的选择标准,但是信息增益倾向于选择特征取值数量较多的特征。C4.5用信息增益率作为待分裂特征的选择标准,可以避免这种倾向。值得注意的是,C4.5在选择连续特征的分裂点位的时候,依然使用信息增益作为选择标准。
X对Y的信息增益率是X对Y的信息增益和X的熵的比值。
04
四,基尼不纯度和基尼不纯度增益
01
基尼不纯度
基尼不纯度和熵具有相似的作用,可以衡量一个随机变量取值的不确定性或者说"不纯净"程度。它满足我们的先验预期,当随机变量只有一种可能取值的时候,基尼不纯度为0,当随机变量的可能取值数量越多,取值概率分布越平均,基尼不纯度越大。
基尼不纯度的定义如下。
基尼不纯度满足我们对不确定性衡量指标的先验假设。事实上,基尼不纯度和熵有非常密切的关系,把熵的对数部分泰勒展开到1阶,即得到基尼不纯度的定义公式。
02
基尼不纯度增益
基尼不纯度增益和信息增益的作用非常类似。计算方法也非常相似。
值得注意的是CART决策树是二叉树,在计算离散特征的基尼不纯度增益时会尝试根据特征是否取某个特定的类别把特征空间分成两部分,而在计算连续特征的基尼不纯度增益时会尝试选择一个分裂点位把特征空间分成两部分。
星标我,每天多一点智慧