TSP问题总结归纳
TSP问题即旅行商问题,经典的TSP可以描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短。从图论的角度来看,该问题实质是在一个带权完全无向图中,找一个权值最小的哈密尔顿回路。
旅行商问题有很多种不同的问法,最近做了几个关于TSP的题,下面总结一下。由于大部分TSP问题都是NP-Hard的,因此很难得到什么高效的多项式级别的算法,一般采用的算法都偏向于暴力搜索以及状压DP,这里都采取用状压DP解决。大部分TSP问题所给的地点数目都非常小。
考虑经典的TSP问题,如果采用状压DP,将每个地点访问与否作为二进制1/0压缩,不难得到状态转移方程:
dp[S][i] = min(dp[S][i], dp[S ^ (1 << (i - 1))][k] + dist[k][i])
S代表当前状态,i(从1开始)表示到达当前状态时最后访问的是第i个地点
k为S中所有访问的与i不同的地点。
dist表示两点间最短路。
以及初始化:
DP[S][i] = dist[start][i](S == 1<<(i - 1))
如果初次遇到状压dp,感到陌生的话,就请仔细思考上面式子的含义,这是大部分TSP问题的关键。
经典TSP——HDU-5067–Harry And Dig Machine
题目链接
题意:给定一个n*m的地图,地图上的数为0表示不需要挖掘,大于0则表示需要挖掘,
现在有一台挖掘机在地图的最左上方的位置,需要将所有需要挖掘的地方挖掘一次,
然后回到地图原点,问挖掘机所走的最短路程是多少?
分析:因为这个题是一个地图,每个位置之间都是连通的,因此不难想到挖掘机走的最短路程肯定是每个挖掘点只走一次的情况,那么本题就是一个典型的TSP问题,地图上没有任何障碍,因此可以直接用两点的 横坐标差的绝对值+纵坐标差的绝对值代表两点之间的距离,然后将每个点的状态压缩,利用状压dp求解即可。
AC代码:
#include
#include
#include
#include
const int maxN = 55;
int dp[1 << 11 ][11];
int dist[11][11];
int pos[11][2];
int min(int a , int b)
{
if (a > b) return b;
return a;
}
void Init(int posNum)
{
for (int i = 0 ; i <= posNum ; i++)
{
for (int j = 1 ; j <= posNum ; j ++ )
{
if ( i == 0 )
{
dist[j][i] = dist[i][j] = pos[j][0] + pos[j][1] - 2;
}
else {
dist[j][i] = dist[i][j] = abs(pos[i][0] - pos[j][0]) + abs(pos[i][1] - pos[j][1]);
}
}
}
}
int main()
{
int n, m;
while (scanf("%d%d",&n,&m)!=EOF)
{
int posNum = 0;
for (int i = 1 ; i <= n ; i ++ )
{
for (int j = 1 ; j <= m ; j ++ )
{
int num;
scanf("%d",&num);
if ( num > 0 )
{
if (i == 1 && j == 1) continue;
posNum++;
pos[posNum][0] = i;
pos[posNum][1] = j;
}
}
}
memset(dist, 0, sizeof(dist));
Init(posNum);
int stateNum = 1 << posNum;
memset(dp, 0, sizeof(dp));
for (int S = 0 ; S < stateNum ; S ++ )
{
for (int i = 1 ; i <= posNum ; i ++ )
{
int tmp = 1 << (i - 1);
if (S & tmp)
{
if (S == tmp)
{
dp[S][i] = dist[0][i];
}
else {
dp[S][i] = 0x3f3f3f3f;
for (int k = 1 ; k <= posNum ; k ++ )
{
if ( (S & (1 << (k - 1) )) && k != i )
{
dp[S][i] = min(dp[S][i], dp[S ^ (1 << (i - 1))][k] + dist[k][i]);
}
}
}
}
}
}
int ans = 1e8;
for (int i = 1 ; i <= posNum ; i ++ )
{
ans = min(ans, dp[stateNum - 1][i] + dist[0][i]);
}
if (ans == 1e8) ans = 0;
printf("%d\n", ans);
}
return 0;
}
需要用bfs处理距离-- POJ 2688–Cleaning Robot
题目链接
题意:
本题和上题类似,也是给定一个地图,给定一个机器人的位置以及一些需要访问的点,求机器人访问所有点,但是不需要回到原点。地图上有一些障碍,障碍位置不能经过。
分析:
由于有障碍的存在无法直接得到每个访问点之间的距离,因此需要用bfs来处理最短路。
后面状压DP即可。
AC代码:
#include
#include
#include
#include
#include
#include
using namespace std;
const int maxW = 25;
const int maxN = 15;
int map[maxW][maxW];
int dirtymap[maxN][2];
int dist[maxN][maxN];
int deltaY[4] = { -1 , 1 , 0 , 0 };
int deltaX[4] = { 0 , 0 , -1 , 1 };
int dsDp[1<<12][maxN];
bool visit[maxW][maxW];
int min(int a, int b)
{
if (a > b) return b;
return a;
}
struct Node
{
int x;
int y;
int step;
};
int getDirtyIndex(int x , int y , int dirtyNum )
{
for (int i = 1 ; i <= dirtyNum ; i ++ )
{
if (dirtymap[i][0] == y && dirtymap[i][1] == x)
{
return i;
}
}
}
bool bfs(int start , int dirtyNum,int width , int height )
{
memset(visit, false, sizeof(visit));
int dir = 0;
int sY = dirtymap[start][0];
int sX = dirtymap[start][1];
visit[sY][sX] = true;
queue nodeQue;
Node startN;
startN.x = sX; startN.y = sY; startN.step = 0;
nodeQue.push(startN);
while (dir < dirtyNum && !nodeQue.empty())
{
Node node = nodeQue.front();
nodeQue.pop();
if (!(node.y == sY&& node.x == sX))
{
if (map[node.y][node.x] == '*')
{
int dirtyIndex = getDirtyIndex(node.x, node.y, dirtyNum);
dist[start][dirtyIndex] = dist[dirtyIndex][start] = node.step;
dir++;
}
else if (map[node.y][node.x] == 'o')
{
dist[0][start] = dist[start][0] = node.step;
dir++;
}
}
for (int i = 0 ; i< 4 ; i ++ )
{
int nX = node.x + deltaX[i];
int nY = node.y + deltaY[i];
if (nX >= 1 && nX <= width && nY >= 1 && nY <= height && map[nY][nX] != 'x' && visit[nY][nX] == false)
{
Node nNode;
nNode.x = nX;
nNode.y = nY;
nNode.step = node.step + 1;
visit[nY][nX] = true;
nodeQue.push(nNode);
}
}
}
return dir == dirtyNum;
}
int dp(int dirtyNum )
{
memset(dsDp, 0, sizeof(dsDp));
int stateNum = 1 << dirtyNum;
for (int i = 0 ; i < stateNum ; i ++ )
{
for (int j = 1 ; j <= dirtyNum ; j ++ )
{
int tmp = 1 << (j - 1);
if ( i & tmp )
{
if ( i == tmp )
{
dsDp[i][j] = dist[0][j];
}
else {
dsDp[i][j] = 1e8;
for (int k = 1 ; k <= dirtyNum ; k ++ )
{
if ( i & ( 1 << (k - 1)) && k != j )
{
dsDp[i][j] = min(dsDp[i ^ (1 << (j - 1))][k] + dist[k][j] , dsDp[i][j]);
}
}
}
}
}
}
int ans = 1e8;
for (int i = 1 ; i <= dirtyNum ; i ++ )
{
ans = min(ans, dsDp[stateNum - 1][i]);
}
return ans;
}
int main()
{
int width, height;
while ( cin >> width >> height && !( width == 0 && height == 0 ))
{
int dirtyNum = 0;
for (int i = 1 ; i <= height ; i ++ )
{
for (int j = 1 ; j <= width ; j ++ )
{
char d;
cin >> d;
map[i][j] = d;
if (d == '*')
{
dirtyNum++;
dirtymap[dirtyNum][0] = i;
dirtymap[dirtyNum][1] = j;
}
else if (d == 'o')
{
dirtymap[0][0] = i;
dirtymap[0][1] = j;
}
}
}
bool suc = true;
for (int i = 0 ; i <= dirtyNum ; i ++ )
{
if (bfs(i,dirtyNum,width,height) == false)
{
suc = false;
break;
}
}
if (!suc) cout << -1 << endl;
else cout << dp(dirtyNum) << endl;
}
}
无上界访问次数的TSP问题——POJ 3311 Hie with the Pie
题目链接
题意:
给定一个图的邻接矩阵,现要求从1号点出发,所有需要访问的点都至少被访问一次之后回到原点,问所走的最短路程是多少。
分析:
注意此题是所有需要访问的点至少访问一次,也就是访问次数无上界,因此在处理每个点之间的最短距离的时候要用Floyd算法,用Floyd算法就代表了访问次数是有可能为多次,其余的依旧正常状压DP。
AC代码:
#include
using namespace std;
const int maxN = 20;
int map[maxN][maxN];
int dp[maxN][65540];
int min(int a, int b)
{
if (a > b) return b;
return a;
}
void floyd(int n)
{
for (int i = 1 ; i <= n ; i ++ )
{
for (int j = 1 ; j <= n ; j ++ )
{
for (int k = 1 ; k <= n ; k ++ )
{
if (map[j][i] + map[i][k] < map[j][k] && i != j && k != j && i != k )
{
map[j][k] = map[j][i] + map[i][k];
}
}
}
}
}
int main()
{
int n;
while (cin >> n && n != 0 )
{
for (int i = 1 ; i <= n + 1 ; i ++ )
{
for (int j = 1; j <= n + 1 ; j ++ )
{
int d;
cin >> d;
map[i][j] = d;
}
}
floyd(n + 1);
int maxS = ( 1 << ( n ) ) ;
for (int j = 0; j < maxS; j++)
{
for (int i = 2 ; i <= n + 1 ; i ++ )
{
if ( j & ( 1 << (i - 2) ))
{
if (j == (1 << (i - 2)))
{
dp[i][j] = map[1][i];
}
else {
dp[i][j] = 1 << 30;
for (int k = 2 ; k <= n + 1 ; k ++ )
{
if ((j & (1 << (k - 2))) && k != i)
{
dp[i][j] = min(dp[i][j],dp[k][j ^ (1 << (i - 2))] + map[k][i]);
}
}
}
}
}
}
int ans = (1 << 31) - 1;
for (int j = 2 ; j <= n + 1 ; j ++ )
{
ans = min(ans,dp[j][(1 << n) - 1] + map[j][1]);
}
cout << ans << endl;
}
return 0;
}
至多访问2次的TSP问题–HDU 3001–Traveling
题目链接
题意:有n个城市,起始在任意一个城市,给出每两个城市之间的一条路的长度,现要求访问所有城市至多两次至少一次所需要的走最短路程。
分析:本题也是不知道最短路,但是不能用Floyd处理,因为这里严格限制了每个城市至多访问2次,用Floyd有可能处理过程中访问了多次,而且这个最短路似乎也不是特别好求,那么就可以穷举所有的情况,有些城市有可能会访问2次,那么把所有的城市访问0、1、2次的情况全部考虑一遍不就行了吗?那么这个题就直接状压DP,问题的关键是如何表示这个访问次数,之前的状压DP都是用2进制表示的,现在需要多一个访问2次的情况,这就是这个题最精妙的地方——采用三进制表示状态,0表示不访问,1表示访问1次,2表示访问2次,具体的看代码吧。
AC代码:
#include
#include
#include
using namespace std;
int three[15];
int map[15][15];
int dp[70000][15];
#define INF 0x3f3f3f3f
int min(int a , int b)
{
if (a < b) return a;
return b;
}
int main()
{
three[0] = 1;
for (int i = 1; i <= 10; i++) three[i] = three[i - 1] * 3;
int n, m;
while (scanf("%d%d",&n,&m) != EOF)
{
int from, to, val;
for (int i = 0; i <= n; i++)
for (int j = 0; j <= n; j++)
map[i][j] = 1e8;
while (m--)
{
scanf("%d%d%d", &from, &to, &val);
from--; to--;
map[from][to] = map[to][from] = min(map[from][to], val);
}
memset(dp, INF, sizeof(dp));
int ans = 1e8;
for (int i = 0; i <= 10; i++) dp[three[i]][i] = 0;
for (int i = 0 ; i < three[n] ; i ++ )
{
bool getAns = true;
for (int j = 0 ; j < n ; j ++)
{
if ( ( (i / three[j]) % 3 ) == 0 )
getAns = false;
}
for (int j = 0 ; j < n ; j ++ )
{
for (int k = 0 ; k < n ; k ++ )
{
if ( ( i / three[k] ) % 3 < 2 && j != k )
{
int u = i + three[k];
dp[u][k] = min(dp[u][k], dp[i][j] + map[k][j]);
}
}
}
if (getAns)
{
for (int j = 0; j < n; j++) ans = min(ans, dp[i][j]);
}
}
if (ans == 1e8) ans = -1;
printf("%d\n", ans);
}
return 0;
}
在三进制下没法做到像二进制那样做位运算,因此稍微麻烦一点。如果题目问至多访问2次、3次、4次……,都可以采用类似的方法解决。
上面这样几种TSP问题都是在访问次数上做一些限制,碰到此类问题,如果能够利用某种方法求出符合题目要求的访问点之间的最短路径,就可以直接先求最短路径,然后按经典TSP问题解决;而如果没有办法求出访问点之间的最短路径,就需要穷举所有的访问方式。
多TSP问题–HDU 4281–Judges’ response
题目链接
题意:
给定n个提问者的坐标以及解答该提问者问题的时间,现有裁判可以解决问题,给出每个裁判为解决问题所能花费的最大时间(所有裁判相同)。
求:
1.至少需要多少个裁判?
2.假设裁判可以有无限个,每个裁判一开始全部位于提问者一的位置,裁判需要回答某几个问题然后回到原处,如何安排裁判解答问题,可以使得裁判走得总路程最少?
分析:
第一问是一个背包问题,将每个提问者的问题是否得到解答作为0/1状态压缩,然后预处理出每个裁判所能达到的所有状态(即在该状态下解答所有需要解答问题的时间不超过裁判所能花费的最大时间),将每种状态看成是背包的物品,状态就是所占的容量,状态转移方程为:
dp[i] = min(dp[i],dp[i ^ state[j]] + 1)(j为合法状态并且i&state[j]==state[j])
第二问就是多TSP问题,在本题中有可能一个裁判无法解决所有的问题,那么如果要解决所有的问题,就可以用多个裁判来解决,由于所有裁判的最大花费时间是相同的,因此可以先求解一次TSP问题,得到每个裁判到达其能到达的状态时所走的最短路程(这个路程就是欧氏距离,不需要特别的处理),然后合并这些状态,best[i]表示状态i下的最短路程,best[i]=min(best[i],best[j]+best[i^j]) j为i的所有子状态,且状态j和状态i^j都是裁判能够到达的状态。
AC代码:
#include
#include
const int maxN = 16;
int cost[maxN + 1];
int dp[70000];
int tspDp[70000][maxN+1];
int best[70000];
int pos[maxN+1][2];
int totalState;
int S[7000];
int dist[maxN+1][maxN+1];
#define INF 1e8
int min(int a , int b )
{
if (a > b) return b;
return a;
}
void InitDist(int n)
{
for (int i = 1; i <= n; i++)
{
for (int j = 1 ; j <= n ; j ++ )
{
int d = (pos[i][0] - pos[j][0]) * (pos[i][0] - pos[j][0]) + (pos[i][1] - pos[j][1]) * (pos[i][1] - pos[j][1]);
dist[i][j] = ceil(sqrt((double)d));
}
}
}
bool check(int state , int n , int maxCost )
{
int sum = 0;
for (int i = 0 ; i < n ; i ++ )
{
if ( state & ( 1 << i ) )
{
sum += cost[i + 1];
}
}
return sum <= maxCost;
}
int dpFunc(int n , int total)
{
for (int i = 0; i < (1 << n); i++)dp[i] = INF;
dp[0] = 0;
for (int i = 1 ; i <= total ; i ++ )
{
for (int j = ( (1 << n) - 1 ) ; j >= 0 ; j -- )
{
if ( ( (j & S[i]) == S[i]) && dp[j ^ S[i]] != INF )
{
dp[j] = min(dp[j], dp[j^S[i]] + 1);
}
}
}
return dp[(1 << n) - 1] == INF ? -1 : dp[(1 << n) - 1];
}
int mtsp(int total , int n )
{
for (int i = 0; i < (1 << n); i++) best[i] = INF;
for (int i = 1 ; i <= total ; i ++ )
{
for (int j = 0 ; j < n ; j ++ )
{
if ( S[i] & ( 1 << j ) )
{
if ( S[i] == ( 1 << j ) )
{
tspDp[S[i]][j] = dist[1][j + 1];
}
else {
tspDp[S[i]][j] = INF;
for (int k = 0 ; k < n ; k ++ )
{
if ( (S[i] & (1 << k)) && k != j )
{
tspDp[S[i]][j] = min(tspDp[S[i]][j], tspDp[S[i] ^ (1 << j)][k] + dist[k+1][j+1]);
}
}
}
best[S[i]] = min(best[S[i]], tspDp[S[i]][j] + dist[j+1][1]);
}
}
}
for(int i = 0 ; i < ( 1 << n) ; i ++ )
{
if ( i & 1 )
{
for (int j = i & ( i - 1 ) ; j ; j = i & ( j - 1 ) )
{
best[i] = min(best[i], best[j] + best[i^j]);
}
}
}
return best[(1 << n) - 1] == INF ? -1 : best[(1 << n) - 1];
}
int main()
{
int n, m;
while ( scanf( "%d%d" ,&n, &m ) != EOF )
{
int x, y;
totalState = 0;
for (int i = 1 ; i <= n ; i ++ )
{
scanf("%d%d", &x, &y);
pos[i][0] = x;
pos[i][1] = y;
}
for (int i = 1 ; i <= n ; i ++ )
{
int c;
scanf("%d", &c);
cost[i] = c;
}
for (int i = 0 ; i < (1 << n) ; i ++ )
{
if (check(i,n,m))
{
totalState++;
S[totalState] = i;
}
}
InitDist(n);
int ans = dpFunc(n, totalState);
int ans2 = mtsp(totalState, n);
printf("%d %d\n", ans, ans2);
}
return 0;
}
POJ 2677–Tour–双调TSP问题
双调TSP问题是比较特殊的TSP问题,它对TSP问题走的路线做了限制:只能从最左端开始出发,然后严格地从左向右走到最右端,再从最右端严格地从右走向左回到出发点,这种问题可以在多项式复杂度内解决。
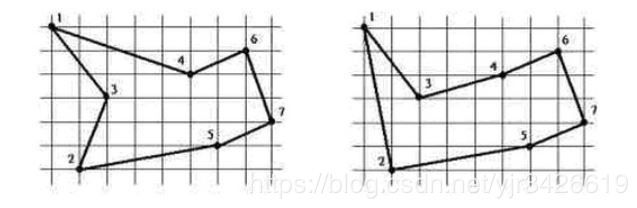
双调TSP其实就是走如图所示的这样一种闭合回路。
设dp[i][j]表示从i出发向左走到1 然后再从1出发向右走到j的最短距离
状态转移,当i
最终答案为dp[n][n] = dp[n-1][n] + dist[n-1][n]
AC代码:
#include
#include
#include
const int maxN = 205;
double min(double a , double b )
{
if (a > b) return b;
return a;
}
double dp[maxN][maxN];
struct Node
{
double x;
double y;
Node() {};
Node(double xx ,double yy)
{
x = xx;
y = yy;
};
bool operator < (const Node & n)
{
return this->x < n.x;
};
};
Node nodeArr[maxN];
double dist(int i , int j )
{
return sqrt((nodeArr[i].x - nodeArr[j].x) * (nodeArr[i].x - nodeArr[j].x) + (nodeArr[i].y - nodeArr[j].y) * (nodeArr[i].y - nodeArr[j].y));
}
int main()
{
int n;
while (scanf("%d", &n) != EOF)
{
for (int i = 1 ; i <= n ; i ++ )
{
double x, y;
scanf("%lf%lf", &x, &y);
nodeArr[i] = Node(x, y);
}
std::sort(nodeArr + 1, nodeArr + n + 1 );
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = 0;
dp[1][2] = dist(1, 2);
for (int i =3 ; i<= n ; i ++ )
{
for (int j = 1 ; j < i - 1 ; j ++ )
{
dp[j][i] = dp[j][i-1] + dist(i-1,i);
}
dp[i - 1][i] = 1e8;
for (int j = 1 ; j < i - 1 ; j ++ )
{
dp[i - 1][i] = min(dp[j][i-1] + dist(i, j),dp[i-1][i]);
}
}
dp[n][n] = dp[n - 1][n] + dist(n - 1, n);
printf("%.2f\n", dp[n][n] );
}
return 0;
}