fpga实现浮点数乘法以及sin运算
一、FPGA表示浮点数的方法
FPGA表示浮点数的方法主要由两个
1 自己定义的 比如最高位位符号位,中间n位为整数部分,最后m位为小数部分
举个例子
3.14 转换位2进制 11.00100011
我们可以表示为这样 0_00000011_00100011
最高位为符号位 中间八位为整数部分,后八位为小数部分
这种定义的方式只有程序员自己知道 在写程序的时候可以随意的定义
2 IEEE浮点数表示方式
对于单精度(float)的数字来说 主要包括 最高位位符号位,中间8位阶码位,最后23位为尾数
还是拿3.14来举例 转换位2进制 11.00100011…
首先必须先将数据转换为1.x * 2^m次的格式 即 1.100100011 * 2^1格式
8位阶码位的大小位 127+1 127为固定的 1为2的指数
尾数就是小数点后面的所有数据 100100011后面补充0 到23位
所以最终表示为 0_10000000_10010001100000000000000 即 十六进制:4048C000(H)
通过计算机计算 发现4048C000对应的小数为3.136719 该误差是由于在计算3.14转换位2进制的时候只取了小数点后的8位,从而精度有了偏差
为了验证该表示方法的正确性 我们将3.14的二进制多取几位
3.14 = 11.001000111101011100001…
同理转换为科学技术法 3.14 = 11.001000111101011100001 = 1.1001000111101011100001 * 2^1
阶码位127+1 = 128
最终表示结果 0_10000000_10010001111010111000010 = 4048F5C2 (H)
经过计算器验证 4048F5C2 (H)对应的小数结果位3.140000 该表示方式正确
二、FPGA浮点乘法运算
我一般采用的浮点运算方式为自定义方式 即自己定义小数点的位置
比如计算 30 * pi/180
30 对应的二进制 00011110
规定A [23:0] [符号位] [22:15]整数位 [14:0] 小数位
则30表示为 24’b0_00011110_000000000000000
pi/180 = 0.0174444444444444对应的二进制 0.000001000111011
照规则B [16:0] [符号位] 15整数位 [14:0] 小数位
则 pi/180表示位17’b0_0_000001000111011
计算过程 30*pi/180 = 24’b0_00011110_000000000000000 * 16’b0_000001000111011
最终结果位24+17bit 即41bit
最关键的一点就是41bit中有多少是整数部分 多少位是小数部分
小数部分的位数是两个数小数部分位数之和 第一个数的小数部分15位 第二个数的小数部分15位
所以最终结果 小数部分共30位
所以最终的表示 [40:0] 40:符号位 [39:30]整数部分 [29:0]小数部分
计算过程
assign result = $signed(A) * $signed(pi_180) //采用有符号数的乘法
得到结果 result = 41’h21750000
三、FPGA的sin运算
在quartus中调用sin的IP核 发现 输入输出数据均为IEEE格式的数据
因此 我们需要将自己定义的数据转换为IEEE浮点型数据
接下来介绍将自己定义的浮点数据转换成IEEE浮点数据
上面计算结果result = 41’h21750000 转换成二进制
100001011101010000000000000000 后面30bit为小数部分
则其实际的含义0_0…0_100001011101010000000000000000
即0.100001011101010000000000000000
转换成科学技术法 1.00001011101010000000000000000 * 2^ (-1)
最高位符号位 0
8位阶码位 127-1
尾数 00001011101010000000000
所以转换成IEEE格式
表示为 0_8’d126_23’b00001011101010000000000000000 = 3F05D4000(H)
FPGA来实现上述格式转换的过程
/******************** 输入为 31符号位 [29:20]整数位 [19:0]小数位 ***********************/
//找到第一个不是0的位数 如果是第30位为1 则偏移的阶码位为9 因为整数部分一共是10位 去掉最高位还余9位
//则最终的8位阶码位为127+9 以此类推
always@(posedge clk)
begin
if (rst_n)
begin
if( y_rad_real[30]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd136,y_rad_real[29:7]};
else if(y_rad_real[29]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd135,y_rad_real[28:6]};
else if(y_rad_real[28]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd134,y_rad_real[27:5]};
else if(y_rad_real[27]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd133,y_rad_real[26:4]};
else if(y_rad_real[26]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd132,y_rad_real[25:3]};
else if(y_rad_real[25]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd131,y_rad_real[24:2]};
else if(y_rad_real[24]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd130,y_rad_real[23:1]};
else if(y_rad_real[23]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd129,y_rad_real[22:0]};
else if(y_rad_real[22]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd128,y_rad_real[21:0],1'b0};
else if(y_rad_real[21]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd127,y_rad_real[20:0],2'b0};
else if(y_rad_real[20]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd126,y_rad_real[19:0],3'b0};
else if(y_rad_real[19]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd125,y_rad_real[18:0],4'b0};
else if(y_rad_real[18]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd124,y_rad_real[17:0],5'b0};
else if(y_rad_real[17]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd123,y_rad_real[16:0],6'b0};
else if(y_rad_real[16]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd122,y_rad_real[15:0],7'b0};
else if(y_rad_real[15]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd121,y_rad_real[14:0],8'b0};
else if(y_rad_real[14]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd120,y_rad_real[13:0],9'b0};
else if(y_rad_real[13]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd119,y_rad_real[12:0],10'b0};
else if(y_rad_real[12]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd118,y_rad_real[11:0],11'b0};
else if(y_rad_real[11]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd117,y_rad_real[10:0],12'b0};
else if(y_rad_real[10]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd116,y_rad_real[9:0],13'b0};
else if(y_rad_real[9]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd115,y_rad_real[8:0],14'b0};
else if(y_rad_real[8]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd114,y_rad_real[7:0],15'b0};
else if(y_rad_real[7]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd113,y_rad_real[6:0],16'b0};
else if(y_rad_real[6]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd112,y_rad_real[5:0],17'b0};
else if(y_rad_real[5]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd111,y_rad_real[4:0],18'b0};
else if(y_rad_real[4]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd110,y_rad_real[3:0],19'b0};
else if(y_rad_real[3]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd109,y_rad_real[2:0],20'b0};
else if(y_rad_real[2]==1'b1)
y_rad_real_float <= {y_rad_real[31],8'd108,y_rad_real[1:0],21'b0};
else
y_rad_real_float <= 32'b0;
end
end
将这个数据输入到sin 的IP核函数的输入口
sin_altfp_sincos_cie sin_U1 (
.clock (clk),
.data (dataIn_float),
.result (dataOut));
输出结果 32’h3effa176 该数据也是IEEE类型的数据 经过计算器转换 可求的该数据代表float 0.499279
计算结果正确
推荐工具
1 浮点数十六进制转换器 强力推荐!!
很好用的软件 直接将小数转换成IEEE格式的浮点格式
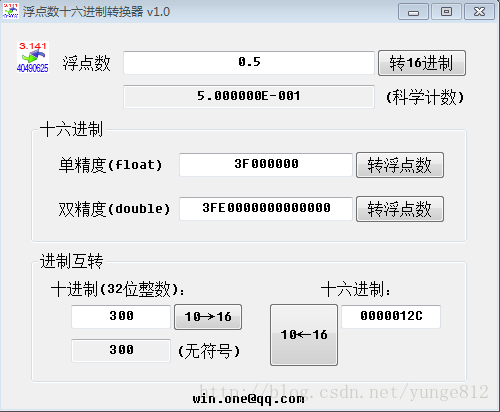
直接输入0.5 即可得到IEEE格式的浮点数十六进制表示法
下载地址 http://download.csdn.net/download/yunge812/10271269
2 进制转换器
可以完成2-63进制类型所有数据的转换
下载地址 http://download.csdn.net/download/yunge812/10271258
整个工程是求取来sin(30*pi/180)的计算过程 仿真结果正确
整个工程的源码下载地址
http://download.csdn.net/download/yunge812/10271282
=======================================================================
最近新开的公众号,文章正在一篇篇的更新,
各位朋友有什么问题了可以直接在上面提问,我会一一进行解答的。
跟着阳光非宅男,一步步走进电子的世界。
关注之后回复 资料下载 关键词可以获得免费海量的视频学习资料下载~~!
已共享的学习视频资料,共享资料正在不断更新中。
共享FPGA视频学习资料:
=======================================================================
