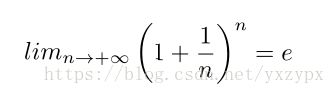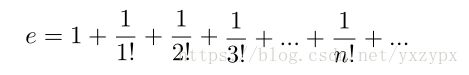刚接触编程的同学可以看看的几个编程练习(python实现)(三)
本大白最近带一只小白入手编程,想法是在练习中学习,所以弄了几个题目。其中不少是经典的练习题,在很多编程入门书籍中都有出现;有的题涉及到一点数据结构的理念。在这里分享出来,刚接触编程的同学可以和我们一起做一做(无论学的是哪种语言都可以看一看,思路是通用的。这里我们学的是python),也欢迎大家指正。
13. 水仙花数
水仙花数是这样的三位数:它的大小 = 个位数字立方 + 十位数字立方 + 百位数字立方
这里可以用到第9题中拆分整数数位的函数
count = 0
for number in range(100, 1000):
condition = 0
for digit in split(number, 3):
condition += digit ** 3
if condition == number:
count += 1
print(str(number) + " ", end = '')
if count % 10 == 0:
print()14. 分解质因数
将一个正整数n分解成质数相乘的形式。这里我的思路是:由于n的质因数必然在小于或等于n的质数中寻找,所以我我们先找出小于或等于n的所有质数。在这些质数中由小到达检测:若某质数i能被n整除,则将i添加到结果中,并取n除以i的商。若商在质数表中(即商是质数),则将商添加进结果,完成分解;否则对商进行类似的操作。
这里寻找小于或等于n的质数采用筛选法(对12题中的函数稍作修改)
import math
def get_prime(n):
number = -1
result = []
table = [False]
for i in range(1, n + 1):
table.append(True)
table[1] = False
table[2] = True
try_num = 2
while try_num <= int(math.sqrt(n)) + 1:
for num in range(try_num + 1, n + 1):
if table[num] == True:
if num % try_num == 0:
table[num] = False
for i in range(try_num + 1, n + 1):
if table[i] == True:
try_num = i
break
for flag in table:
number += 1
if flag:
result.append(number)
return result
def get_decompose(n):
if n == 1:
return
elif n == 2:
return [2]
result = []
primes = get_prime(n)
remain = n
run = True
while run:
if remain == 1:
run = False
elif remain == 2:
result.append(remain)
run = False
else:
#primes = get_prime(remain)
for prime in primes:
if remain % prime == 0:
result.append(prime)
remain = int(remain / prime)
break
if remain in primes:
result.append(remain)
run = False
return result
# example
get_decompose(2)
get_decompose(100)
get_decompose(17)
get_decompose(12345)
get_decompose(126) 15. 完数
完数是这样的数:它的大小等于它的所有小于它本身的因数之和,如6的小于它本身的因素有1, 2, 3, 且 1 + 2 + 3 = 6。
一个函数返回某个整数的小于它本身的所有因数;主要的函数调用该函数,并判断因数之和是否等于该整数。
import math
def get_factor(n):
result = []
for i in range(1, int(n / 2) + 1):
if n % i == 0:
result.append(i)
return result
get_factor (20)
get_factor(24)
get_factor(17)
get_factor(2)
def get_complete_number(n):
result = []
for number in range(2, n + 1):
if number == sum(get_factor(number)):
result.append(number)
return result
# 例
get_complete_number(1000)
get_complete_number(10000) 16. 计算阶乘
法一: 按阶乘的定义计算
法二: 递归法。若n等于1,则返回1,否则返回n乘以n-1的阶乘。
法三: 改进的递归。与法二相比,递归的部分除了调用函数递归外,不进行额外操作,这样可以减少堆栈的调用。
n = int(input("Enter an integer: "))
print(str(n) + "! = " + str(factorial_1(n)))
### 17.1 阶乘定义法
def factorial_1(n):
if n == 0:
return 1
else:
result = 1
for i in range(1, n+1):
result *= i
return result
### 17.2 递归法
def factorial_2(n):
if n == 1:
return 1
else:
return n * factorial_2(n - 1)
### 7.3 改进递归法
def factorial_3(n, m = 1):
if n == 1:
return m
else:
return factorial_3(n - 1, m * n)17. 估计e
法一: 利用极限的重要等式
法二: 利用级数
我们也可以比较达到相同精度时,法一与法二中需要的n的大小
### 17.1 重要等式
epsilon = 1e-6
x = 1
count_1 = 1
result_1 = (1 + x) ** (1 / x)
result_2 = 0
while abs(result_1 - result_2 >= epsilon):
count_1 += 1
x /= 2
result_2 = result_1
result_1 = (1 + x) ** (1 / x)
print(result_1)
print(count_1)
### 17.2 级数
epsilon = 1e-6
n = 1
result_3 = 1 + 1/factorial_3(n)
result_4 = 0
while(abs(result_3 - result_4) >= epsilon):
n += 1
result_4 = result_3
result_3 += 1/factorial_3(n)
print(result_3)
print(n) 18. 估计pi
法一: 利用级数
法二: 蒙特卡洛模拟。设坐标平面上,有一圆心在原点、半径为1的圆,另有该圆的外接正方形。设想我们在正方形中随机“投射”很多点,则有的落在圆外,有的落在圆内或圆上。(由几何概型及大数定理)当投射的点足够多时,落在圆内或圆上的点的比例,近似等于(依概率收敛)到圆面积与正方形面积的比。
我们可以产生服从(-1, 1)间均匀分布的随机数x, y,将(x, y)作为“投射点”。(x, y)到原点的距离 <= 1即为落在圆内或圆上。
法三: 改进的蒙特卡洛模拟。原理上与法二一致,但在随机数的产生上作了改进(蒙特卡洛模拟方差缩减技术)
### 18.1 级数法
epsilon = 1e-6
n = 1
count_1 = 1
signal = 1
result_1 = signal * (1 / n)
result_2 = 0
while(abs(result_1 - result_2) >= epsilon):
count_1 += 1
n += 2
signal *= -1
result_2 = result_1
result_1 += signal * (1 / n)
print(4 * result_1)
print(count_1)
### 18.2 蒙特卡洛模拟
import random
times = 5000
count = 0;
for i in range(times + 1):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x ** 2 + y ** 2 <= 1:
count += 1
print(4 * count / times)
### 18.3 蒙特卡洛模拟改进*
import math
count_2 = 0;
for i in range(1, times + 1):
u = random.uniform(0, 1)
count_2 += (math.sqrt(1 - ((u + i - 1) / times) ** 2 )
+ math.sqrt(1 - ((i - u) / times) ** 2))
print(4 * count_2 / (times * 2))这里我同样模拟5000次,改进前的结果(法二)为3.112,改进后的结果(法三)为3.1415932936213644,可见精度的显著差别。
后续部分请见 刚接触编程的同学可以看看的几个编程练习(python实现)(四)