二维离散余弦变换（DCT）与二维离散反余弦变换（IDCT）C语言实现

二维离散余弦变换（DCT）与二维离散反余弦变换（IDCT）C语言实现

实验目标

对一个8x8的矩阵进行DCT和IDCT然后在观察前者和后者的变化

实验准备

理论基础

二维离散余弦变换

$$F(u,v)=c(u)c(v)\sum _{i=0}^{N-1}\sum _{i=0}^{N-1}f(i,j)\cos [\frac{(i+0.5)\pi }{N}u]\cos [\frac{(i+0.5)\pi }{N}v]$$
$$c(u)=\{\begin{array}{ll}\sqrt{\frac{1}{N}},& u=0\\ \sqrt{\frac{2}{N}},& u\ne 0\end{array}$$
二维离散反余弦变换
$$f(i,j)=\sum _{u=0}^{N-1}\sum _{v=0}^{N-1}c(u)c(v)F(u,v)\cos [\frac{(i+0.5)\pi }{N}u]\cos [\frac{(j+0.5)\pi }{N}v]$$
$$c(u)=\{\begin{array}{ll}\sqrt{\frac{1}{N}},& u=0\\ \sqrt{\frac{2}{N}},& u\ne 0\end{array}$$

具体公式理解就不讲了，高中知识就可以理解

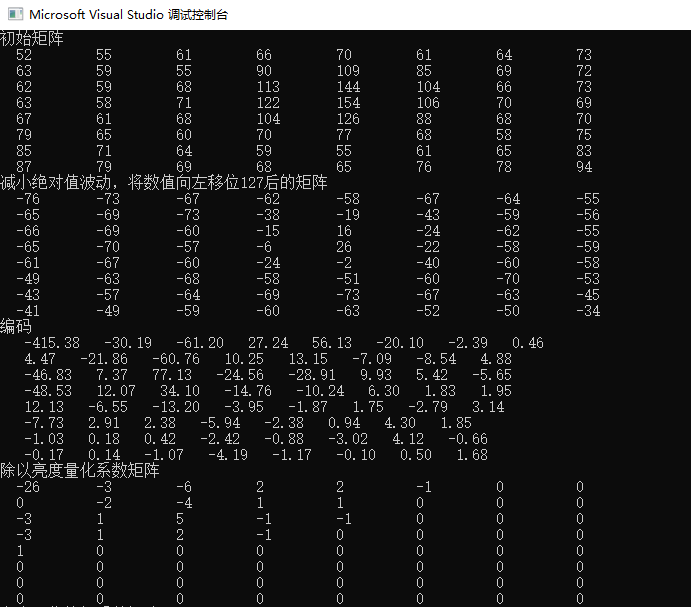
实验结果

实验过程

/*
剑一
blog: www.leon7777.online  
github:www.github.com/zpf996
emil: [email protected]

步骤：
1、向左位移127
2、编码：DCT变换
3、除以量化矩阵
4、解码：IDCT变换
5、向右位移127
*/

#include
#include

#define PI 3.1415926

//矩阵
int fre[8][8];
int temp[8][8];
float t[8][8];

//向左移位127
int move(int fre[8][8])
{

	int i, j = 0;
	for (i = 0; i < 8; i++)
	{
		for (j = 0; j < 8; j++)
		{
			temp[i][j] = fre[i][j] - 128;
		}
	}
	pr(temp);
}
//向右移位127
int Imove(int fre[8][8])
{

	int i, j = 0;
	for (i = 0; i < 8; i++)
	{
		for (j = 0; j < 8; j++)
		{
			temp[i][j] = fre[i][j] + 128;
		}
	}
	pr(temp);
}
//离散余弦变换
float DCT(int f[8][8], int k, int l)
{
	int i, j = 0;
	float p1=0, p2=0;
	float factor;
	float sum = 0;
	float data_dct;
	if (k == 0)
	{
		if (l == 0)
		{
			factor = 1.0 / 8;
		}
		else
		{
			factor = sqrt(2.0) / 8;
		}

	}
	else
	{
		if (l == 0)
		{
			factor = sqrt(2.0 )/ 8;
		}
		else
		{
			factor = 2.0 / 8;
		}
	}
	for (i = 0; i < 8; i++)
	{
		for (j = 0; j < 8; j++)
		{
			p1 = cos(((2 * i + 1)*k*PI) / 16.0);
			p2 = cos(((2 * j + 1)*l*PI) / 16.0);
			sum = sum + f[i][j] * p1*p2;
		}
	}
	data_dct = sum * factor;
	return data_dct;
}
//四舍五入
int rounding(float a)
{
	if (a >= 0)
	{
		return (int)(a + 0.5);
	}
	else
	{
		return (int)(a - 0.5);
	}

}
//反离散余弦变换
float IDCT(int f[8][8], int k, int l)
{
	int u, v = 0;
	float p1, p2;
	float factor;
	float sum = 0;
	float data_dct;
	for (u = 0; u < 8; u++)
	{
		for (v = 0; v < 8; v++)
		{
			if (u == 0)
			{
				if (v == 0)
				{
					factor = 1.0 / 8;
				}
				else
				{
					factor = sqrt(2.0) / 8;
				}
			}
			else
			{
				if (v == 0)
				{
					factor = sqrt(2.0 )/ 8;
				}
				else
				{
					factor = 2.0 / 8;
				}

			}
			p1 = ((2 * k + 1)*u*PI) / 16.0;
			p2 = ((2 * l + 1)*v*PI) / 16.0;
			sum = sum + factor *f[u][v] * cos(p1)*cos(p2);

		}
	}
	data_dct = sum;
	return data_dct;
}
//编码
int coding(float fre[8][8])
{
	int k, l = 0;
	for (k = 0; k < 8; k++)
	{
		for (l = 0; l < 8; l++)
		{
			t[k][l] = DCT(fre, k, l);
			printf("   %.2f", t[k][l]);
		}
		printf("\n");
	}
	
}
//亮度化系数矩阵
int LQ(float f[8][8], int lq[8][8])
{

	int i, j = 0;
	for (i = 0; i < 8; i++)
	{
		for (j = 0; j < 8; j++)
		{
			temp[i][j] = rounding(f[i][j] / lq[i][j]);
		}
	}
	pr(temp);
}
//亮度化恢复系数矩阵
int ILQ(int fre[8][8], int lq[8][8])
{

	int i, j = 0;
	for (i = 0; i < 8; i++)
	{
		for (j = 0; j < 8; j++)
		{
			temp[i][j] = fre[i][j] * lq[i][j];
		}
	}
	pr(temp);
}
//解码
int decoding(int f[8][8])
{

	int k, l = 0;
	for (k = 0; k < 8; k++)
	{
		for (l = 0; l < 8; l++)
		{
			fre[k][l] = rounding(IDCT(f, k, l));
		}
	}
	pr(fre);
}
//输出
int pr(int fre[8][8])
{
	int i, j = 0;
	for (i = 0; i < 8; i++)
	{
		for (j = 0; j < 8; j++)
		{
			printf("  %-8d", fre[i][j]);
		}
		printf("\n");
	}
}
int main()
{

	//亮度系数矩阵
	int Lq[8][8] = { {16,11,10,16,24,40,51,61},
					{12,12,14,19,26,58,60,55},
					{14,13,16,24,40,57,69,56},
					{14,17,22,29,51,87,80,62},
					{18,22,37,56,68,109,103,77},
					{24,35,55,64,81,104,113,92},
					{49,64,78,87,103,121,120,101},
					{72,92,95,98,112,100,103,99} };
	//初试矩阵
	int data[8][8] = {  {52,55,61,66,70,61,64,73},
						{63,59,55,90,109,85,69,72},
						{62,59,68,113,144,104,66,73},
						{63,58,71,122,154,106,70,69},
						{67,61,68,104,126,88,68,70},
						{79,65,60,70,77,68,58,75},
						{85,71,64,59,55,61,65,83},
						{87,79,69,68,65,76,78,94} };
	printf("初始矩阵\n");
	pr(data);

	printf("减小绝对值波动，将数值向左移位127后的矩阵\n");
	//减小绝对值波动，将数值向左移位128
	move(data);


	printf("编码\n");
	//编码
	coding(temp);


	printf("除以亮度量化系数矩阵\n");
	//除以亮度量化系数矩阵
	LQ(t, Lq);


	printf("亮度量化恢复系数矩阵\n");
	//亮度量化恢复系数矩阵
	ILQ(temp, Lq);


	printf("解码\n");
	//解码
	decoding(temp);


	printf("右移127\n");
	//右移127
	Imove(fre);

	printf("初始矩阵\n");
	pr(data);

}