数据拟合与插值方法
- 插值方法
- interp1一维数据插值函数
- csape
- interp2函数二维数据内插值
- interp3函数三维数据插值
- interpn函数n维数据插值
- 二维插值interp2与griddata的区别
- Example
- 拟合方法
- 线性拟合函数regress
- Example
- 多项式曲线拟合函数polyfit
- 多项式曲线求值函数polyval
- 多项式曲线拟合的评价和置信区间函数polyconf
- 稳健回归函数robust
- 向自定义函数拟合nlinfit
- Example
- 线性拟合函数regress
插值方法
interp1——一维数据插值函数
一维数据插值。该函数对数据点之间计算内插值,它找出一元函数f(x)在中间点的数值,其中函数表达式由所给数据决定。
yi=interp1(x,Y,xi):返回插值向量yi,每一元素对应于参量xi,同时由向量X与Y的内插值决定。参量x 指定数据Y的点。若Y为一矩阵,则按Y的每列计算。yi是阶数为length(xi)*size(Y,2)的输出矩阵。
yi=interp1(Y,xi):假定x=1:N,其中N为向量Y的长度,或者为矩阵Y的行数。
yi=interp1(x,Y,xi,method):用指定的算法计算插值。nearest为最近邻点插值,直接完成计算;linear为线性插值(默认方式),直接完成计算;spline为三次样条函数插值。
yi=interp1(x,Y,xi,method,’extrap’):对于超出x范围的xi中的分量将执行特殊的外插值法extrap。
yi=interp1(x,Y,xi,method,extrapval):确定超出x范围的xi中的分量的外插值extrapval,其值通常取NaN或0。
csape
pp = csape(x,y,conds,valconds)
其中(x,y)为数据向量,conds表示变界类型, valconds表示边界值。
边界类型(conds)可为:
‘complete’,给定边界一阶导数.
‘not-a-knot’,非扭结条件,不用给边界值.
‘periodic’,周期性边界条件,不用给边界值.
‘second’,给定边界二阶导数.
‘variational’,自然样条(边界二阶导数为0)
边界类型(valconds)可为:
‘complete’,给定边界一阶导数.
‘not-a-knot’,非扭结条件,不用给边界值.
‘periodic’,周期性边界条件,不用给边界值.
‘second’,给定边界二阶导数.
‘variational’,自然样条(边界二阶导数为0)
interp2函数——二维数据内插值
完成二维的数据插值。
ZI=interp2(X,Y,Z,XI,YI):返回矩阵ZI,其元素包含对应于参量XI与YI(可以是向量、或同型矩阵)的元素。用户可以输入行向量 和列向量Xi与Yi,此时,输出向量Zi与矩阵meshgrid(xi,yi)是同型的。同时取决于由输入矩阵X、Y与Z确定的二维函数 Z=f(X,Y)。
ZI=interp2(Z,XI,YI):默认地,X=1:n、Y=1:m,其中[m,n]=size(Z)。再按第一种情形进行计算。
ZI=interp2(Z,n):作n次递归计算,在Z的每两个元素之间插入它们的二维插值,这样,Z的阶数将不断增加。interp2(Z)等价于interp2(z,1)。
ZI=interp2(X,Y,Z,XI,YI,method):用指定的算法method计算二维插值。linear为双线性插值算法(默认算法),nearest为最临近插值,spline为三次样条插值,cubic为双三次插值。
interp3函数——三维数据插值
完成三维数据插值。
VI=interp3(X,Y,Z,V,XI,YI,ZI):求出由参量X,Y,Z决定的三元函数V=V(X,Y,Z)在点(XI,YI,ZI)的值。参 量XI,YI,ZI是同型阵列或向量。若向量参量XI,YI,ZI是不同长度、不同方向(行或列)的向量,这时输出参量VI与Y1,Y2,Y3为同型矩 阵。Y1,Y2,Y3为用函数meshgrid(XI,YI,ZI)生成的同型阵列。若插值点(XI,YI,ZI)中有位于点(X,Y,Z)之外的点,则 相应地返回特殊变量值NaN。
VI=interp3(V,XI,YI,ZI):默认地,X=1:N,Y=1:M,Z=1:P,其中,[M,N,P]=size(V),再按上面的情形计算。
VI=interp3(V,n):作n次递归计算,在V的每两个元素之间插入它们的三维插值。这样,V的阶数将不断增加。interp3(V)等价于interp3(V,1)。
VI=interp3(…,method):用指定的算法method做插值计算。linear为线性插值(默认算法),cubic为三次插值,spline为三次样条插值,nearest为最邻近插值。
interpn函数——n维数据插值
完成n维数据插值。
VI=interpn(X1,X2,…,Xn,V,Y1,Y2,..,Yn):返回由参量X1,X2,..,Xn,V确定的n元函数 V=V(X1,X2,..,Xn)在点(Y1,Y2,…,Yn)处的插值。参量Y1,Y2,…,Yn是同型的矩阵或向量。若 Y1,Y2,…,Yn是向量,则可以是不同长度,不同方向(行或列)的向量。
VI=interpn(V,Y1,Y2,…,Yn):默认地,X1=1:size(V,1),X2=1:size(V,2),…,Xn=1:size(V,n),再按上面的情形计算。
VI=interpn(V,ntimes):作ntimes递归计算,在V的每两个元素之间插入它们的n维插值。这样,V的阶数将不断增加。interpn(V)等价于interpn(V,1)。
二维插值,interp2与griddata的区别
interp2的插值数据必须是矩形域,一般使用meshgid生成的
而griddata函数的插值数据X和Y没有那么多数据,特别是对试验中随机没有规律采取的数据进行插值具有很好的效果
griddata(X,Y,xi,yi,’v4’) v4是一种插值算法,没有具体的名字,一般认为是最好的
X和Y提供的已知数据点,xi和yi是需要插值的数据点,一般使用meshgrid生成,当然也可以其他数据,但是那样绘图的时候就比较麻烦,不能使用mesh等,只能使用trimesh
Example:
x=[0,0.25 ,0.5,0.75,1];
y=[620,700,800,900,1000];
z=[0.00214 0.01025 0.01681 0.02331 0.02644
0.00236 0.01039 0.01717 0.02375 0.02711
0.00286 0.01058 0.01739 0.02411 0.02792
0.00328 0.01072 0.01747 0.02442 0.02878
0.00369 0.0108 0.01761 0.02481 0.0295 ];
xi=linspace(0,1,100);
yi=linspace(600,1000,80);
[xii,yii]=meshgrid(xi,yi);
zii=interp2(x,y,z,xii,yii,'linear');
zii1=interp2(x,y,z,xii,yii,'spline');
zii2=interp2(x,y,z,xii,yii,'nearest');
zii3=griddata(x,y,z,xii,yii,'v4');
subplot(2,2,1);%将区域分为2x2并取第一个区域
mesh(xii,yii,zii),title('interp2 线性插值');画图并设置标题
subplot(2,2,2);mesh(xii,yii,zii1),title('interp2 三次样条插值');
subplot(2,2,3);mesh(xii,yii,zii2),title('interp2 临近点插值');
subplot(2,2,4);mesh(xii,yii,zii3),title('griddata'); 拟合方法
线性拟合函数:regress()
调用格式: b=regress(y,X)
[b,bint,r,rint,stats]= regress(y,X)
[b,bint,r,rint,stats]= regress(y,X,alpha)
说明:b=regress(y,X)返回X与y的最小二乘拟合值,及线性模型的参数值β、ε。该函数求解线性模型:
y=Xβ+ε
β是p´1的参数向量;ε是服从标准正态分布的随机干扰的n´1的向量;y为n´1的向量;X为n´p矩阵。
bint返回β的95%的置信区间。r中为形状残差,rint中返回每一个残差的95%置信区间。Stats向量包含R2统计量、回归的F值和p值。
Example:
当x为1到33时Y为
y=[3.73 6.27 5.93 5.77 5.72 5.80 5.87 5.78 5.96 6.03 6.50 7.00 6.80 6.68 7.03 7.67 7.59 6.96 7.17 6.99 7.17 6.99 6.64 6.71 7.01 7.40 7.49 7.75 8.17 8.09 8.11 8.48 8.99]
y=[3.73 6.27 5.93 5.77 5.72 5.80 5.87 5.78 5.96 6.03 6.50 7.00 6.80 6.68 7.03 7.67 7.59 6.96 7.17 6.99 7.17 6.99 6.64 6.71 7.01 7.40 7.49 7.75 8.17 8.09 8.11 8.48 8.99];
x=[ones(33,1) (1:33)'];
[b,bint,r,rint,stats]= regress(y',x);
b =
5.2904
0.0921
bint =
4.9201 5.6608
0.0731 0.1111
r =
-1.6525
0.7954
0.3633
0.1112
-0.0309
-0.0430
-0.0651
-0.2472
-0.1593
-0.1814
0.1965
0.6044
0.3123
0.1002
0.3581
0.9060
0.7339
0.0118
0.1297
-0.1423
-0.0544
-0.3265
-0.7686
-0.7907
-0.5828
-0.2849
-0.2870
-0.1191
0.2088
0.0367
-0.0354
0.2425
0.6604
rint =
-2.4339 -0.8712
-0.1605 1.7513
-0.6338 1.3604
-0.8993 1.1216
-1.0467 0.9849
-1.0630 0.9770
-1.0888 0.9586
-1.2705 0.7761
-1.1881 0.8695
-1.2124 0.8496
-0.8365 1.2295
-0.4084 1.6172
-0.7203 1.3450
-0.9396 1.1400
-0.6746 1.3909
-0.0796 1.8917
-0.2716 1.7395
-1.0301 1.0537
-0.9105 1.1700
-1.1815 0.8968
-1.0935 0.9846
-1.3570 0.7039
-1.7638 0.2265
-1.7810 0.1996
-1.5902 0.4245
-1.3069 0.7370
-1.3054 0.7313
-1.1383 0.9000
-0.8041 1.2217
-0.9745 1.0479
-1.0416 0.9708
-0.7543 1.2393
-0.3037 1.6245
stats =
0.7591 97.6636 0.0000 0.2598
plot(x,y2,x,y,'go');
即回归方程为:y= 5.2904+0.0921x,置信度为0.75.

多项式曲线拟合函数:polyfit( )
调用格式: p=polyfit(x,y,n)
[p,s]= polyfit(x,y,n)
说明:x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。矩阵s用于生成预测值的误差估计。
多项式曲线求值函数:polyval()
调用格式: y=polyval(p,x)
[y,DELTA]=polyval(p,x,s)
说明:y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。
[y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y DELTA。它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。则Y DELTA将至少包含50%的预测值。
%使用上面的例子
y=[3.73 6.27 5.93 5.77 5.72 5.80 5.87 5.78 5.96 6.03 6.50 7.00 6.80 6.68 7.03 7.67 7.59 6.96 7.17 6.99 7.17 6.99 6.64 6.71 7.01 7.40 7.49 7.75 8.17 8.09 8.11 8.48 8.99];
x=[ones(33,1) (1:33)'];
p=polyfit(x,y,6)
p =
-0.0000 0.0001 -0.0028 0.0528 -0.4775 2.0159 2.7873
xi=linspace(1,33,100);%1到33等分取100个数
z=polyval(p,xi);%求算出的多项式的对应x的值
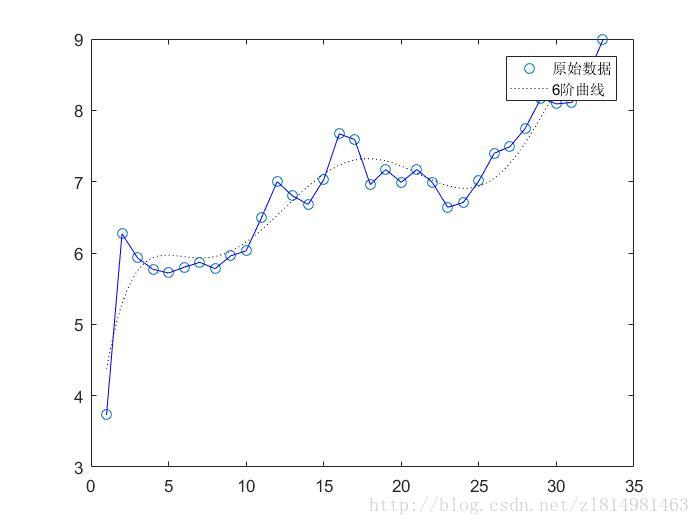
plot(x,y,'o',xi,z,'k:',x,y,'b')%画原始数据点,原始折线,和拟合后的曲线
legend('原始数据','6阶曲线')即多项式方程为:y= 0.0001x^5-0.0028x^4+0.0528x^3-0.4775x^2+2.0159x+2.7873
多项式曲线拟合的评价和置信区间函数:polyconf( )
调用格式: [Y,DELTA]=polyconf(p,x,s)
[Y,DELTA]=polyconf(p,x,s,alpha)
说明:[Y,DELTA]=polyconf(p,x,s)使用polyfit函数的选项输出s给出Y的95%置信区间Y DELTA。它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。1-alpha为置信度。
%使用上面的例子
%继续上面的图像做置信区间
[p s]=polyfit(x,y,6);
[Y,DELTA]=polyconf(p,x,s,0.05);
z=polyval(p,xi);%求算出的多项式的对应x的值
plot(x,y,'o',xi,z,'k:',x,y,'b');%画原始数据点,原始折线,和拟合后的曲线
legend('原始数据','10阶曲线');
hold on
plot(x,Y-DELTA,'r',x,Y+DELTA,'r');%画置信区间稳健回归函数:robust( )
稳健回归是指此回归方法相对于其他回归方法而言,受异常值的影响较小。
调用格式: b=robustfit(x,y)
[b,stats]=robustfit(x,y)
[b,stats]=robustfit(x,y,’wfun’,tune,’const’)
说明:b返回系数估计向量;stats返回各种参数估计;’wfun’指定一个加权函数;tune为调协常数;’const’的值为’on’(默认值)时添加一个常数项;为’off ’时忽略常数项。
%使用上面的例子
y=[3.73 6.27 5.93 5.77 5.72 5.80 5.87 5.78 5.96 6.03 6.50 7.00 6.80 6.68 7.03 7.67 7.59 6.96 7.17 6.99 7.17 6.99 6.64 6.71 7.01 7.40 7.49 7.75 8.17 8.09 8.11 8.48 8.99];
x=1:33;
scatter(x,y);%画图,离散点
hold on;
p=regress(y',[ones(33,1) x']);%线性拟合
r=robustfit(x,y);%稳健拟合
plot(x,p(1)+p(2)*x,':',x,r(1)+r(2)*x,'r');%画图
legend('原始数据','线性拟合','稳健拟合')%设置图例
分析:稳健拟合(实线)对数据的拟合程度好些,忽略了异常值。最小二乘拟合(点线)则受到异常值的影响,向异常值偏移。
向自定义函数拟合nlinfit( )
对于给定的数据,根据经验拟合为带有待定常数的自定义函数。
调用格式: [beta,r,J]=nlinfit(X,y,’fun’,betao)
说明:beta返回函数’fun’中的待定常数;r表示残差;J表示雅可比矩阵。X,y为数据;‘fun’自定义函数;beta0待定常数初值。
Example:
%新建一个脚本
function y=Fun(beta0,x)
a=beta0(1);
b=beta0(2);
y=a+(0.49-a)*exp(-b*(x-8));
%命令行
x=[8.00 8.00 10.00 10.00 10.00 10.00 12.00 12.00 12.00 14.00 14.00 14.00...
16.00 16.00 16.00 18.00 18.00 20.00 20.00 20.00 20.00 22.00 22.00 24.00...
24.00 24.00 26.00 26.00 26.00 28.00 28.00 30.00 30.00 30.00 32.00 32.00...
34.00 36.00 36.00 38.00 38.00 40.00 42.00]';
y=[0.49 0.49 0.48 0.47 0.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.43 0.44 0.43...
0.43 0.46 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.40 0.41 0.41...
0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.39 0.39]';
beta0=[0.30 0.02];//a,b初始值
betafit = nlinfit(x,y,'Fun',beta0);
betafit =
0.3896 0.1011
%即a=0.3896 b=0.1011
plot(x,y,'go',x,Fun(betafit,x),'r')%画图

