Tyvj NOIP全真模拟系列赛（1）游记

谜一样地就被拉过来做什么“全真模拟赛”（赛后证明是PJ难度的）
什么破OJ…
评测机似乎回家过中秋了，做到一半又说不要在网站上提交，一开始说用word发邮箱（exm？），然后又说用比赛格式发邮箱，还要开文件读写，然而压缩包的形式坑倒了一片人，不过据说管理员在后来整理了一下（没有卵用）。
先放上谜一样的rank，壮哉我大机房

T1 算

【问题背景】

zhx帮他妹子做数学题。

【问题描述】

求：
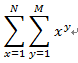
如N=3,M=3，这个值为 11+12+13+21+22+23+31+32+33=56 。 【输入格式】 仅一行，包含两个数N和M.

【输入格式】

仅一行，包含两个数N和M.

【输出格式】

仅一行，包含所求的答案mod 109+7 的值。

【样例输入】

3 3

【样例输出】

56

【数据范围与规定】

对于50%的数据，所有 1≤N,M≤1000 。
对于100%的数据，所有 1≤N,M≤50000 。

Solution：
T1什么水题…
显然等比数列公式搞一搞就好了，除法再加个逆元。

#include
#define P 1000000007
int fast(int a,int b){
    int res=1;
    while(b){
        if(b&1)res=1LL*res*a%P;
        b>>=1;
        a=1LL*a*a%P;
    }
    return res;
}
int main(){
//  freopen("sum.in","r",stdin);
//  freopen("sum.out","w",stdout);
    int n,m,ans=0;
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;i++){
        if(i==1)ans+=m;
        int x=1LL*i*(fast(i,m)-1+P)%P;
        ans=(ans+1LL*x*fast(i-1,P-2))%P;
    }
    printf("%d\n",ans%P);
    return 0;
}

T2 游

【问题背景】

zhx和他的妹子出去玩。

【问题描述】

zhx和他的妹子去一个国家旅游，共有 N 个旅游景点， N−1 条双向连接的道路将它们联通起来，每一条道路有固定长度。一开始zhx位于1号景点。
现在希望你能够求出旅行长度最小的方案，使得每个景点至少被访问到一次。

【输入格式】

第一行两个整数 N ，代表景点数目。
接下来 N−1 行，每行三个整数 s , t , w ，表示有一条从 s 到 t 的双向道路，长度为 w 。 s 和 t 的编号从1开始。

【输出格式】

一行一个整数，代表能够访问每个景点至少一次的方案的最小旅行长度。

【样例输入】

3
1 2 3
2 3 3

3
1 2 3
1 3 3

【样例输出】

6
9

【数据范围与规定】

对于30%的数据， 1≤N≤10 。
对于70%的数据， 1≤N≤1000 。
对于100%的数据， 1≤N≤50000，1≤w≤1000 。

Solution：
T2什么水题…
答案等于所有边权之和的两倍减掉最长的从1出发的一条链的长度。
真的不放心写个树形dp也没事。

#include
#include
#include
#define M 50005
using namespace std;
struct Node{
    int to,w;
};
vectorG[M];
int dis[M];
void dfs(int x,int fa){
    for(int i=0;iint to=G[x][i].to;
        if(to==fa)continue;
        dfs(to,x);
        dis[x]=max(dis[x],dis[to]+G[x][i].w);
    }
}
int main(){
//  freopen("tour.in","r",stdin);
//  freopen("tour.out","w",stdout);
    int n,sum=0;
    scanf("%d",&n);
    for(int i=1;iint a,b,c;
        scanf("%d %d %d",&a,&b,&c);
        sum+=c;
        G[a].push_back((Node){b,c});
        G[b].push_back((Node){a,c});
    }
    dfs(1,-1);
    printf("%d\n",sum*2-dis[1]);
    return 0;
}

T3 幸运数

【问题背景】

zhx和妹子们玩数数游戏。

【问题描述】

仅包含4或7的数被称为幸运数。
一个序列的子序列被定义为从序列中删去若干个数，剩下的数组成的新序列。两个子序列被定义为不同的当且仅当其中的元素在原始序列中的下标的集合不相等。对于一个长度为N的序列，共有 2N 个不同的子序列。（包含一个空序列）。
一个子序列被称为不幸运的，当且仅当其中不包含两个相同的幸运数。
对于一个给定序列，求其中长度恰好为K的不幸运子序列的个数，答案mod 109+7 输出。

【输入格式】

第一行两个正整数N，K，表示原始序列的长度和题目中的K。
接下来一行N个整数ai，表示序列中第i个元素的值。

【输出格式】

仅一个数，表示不幸运子序列的个数。（mod 10^9+7）

【样例输入】

3 2
1 1 1

4 2
4 7 4 7

【样例输出】

3
4

【样例解释】

对于样例1，每个长度为2的子序列都是符合条件的。
对于样例2，4个不幸运子序列元素下标分别为：{1, 2}, {3, 4}, {1, 4}, {2, 3}。注意下标集{1, 3}对应的子序列不是“不幸运”的，因为它包含两个相同的幸运数4.

【数据范围与规定】

对于50%的数据， 1≤N≤16 。
对于70%的数据， 1≤N≤1000,ai≤10000 。
对于100%的数据， 1≤N≤100000,K≤N,1≤ai≤109 。

Solution：
首先，本题的幸运数最多只有一千多个吧，先把这些幸运数处理出来，用map随便搞搞，处理出每一个幸运数的个数。
对于不是幸运数的剩下 d 个数来说，这就是一个组合问题了。因此总方案数为：（设幸运数种数为 tot ，非幸运数个数为 d ）

∑i=1min(tot,k)Ck−id∗calc(tot,i)

然后，对于这个calc数组，显然是一个简单的dp了。设 dp[i][j] 表示从前i种幸运数中取出j个数的方案数。因为一种幸运数要么取一个要么不取，dp方程即为：（ C[i] 表示映射后的第i种幸运数的个数）。

dp[i][j]=dp[i−1][j]+dp[i−1][j−1]∗C[i]

初值即为

dp[i][0]=1(0<=i<=tot)

然后就解决了这个问题，复杂度 O(n+m2) 。

#include
#include
#include
#include
#define M 100005
#define P 1000000007
using namespace std;
map<int,int>mp;
int fact[M],dp[2000][2000],A[M],C[M];
bool check(int x){
    if(x==0)return false;
    while(x){
        int d=x%10;
        if(d!=4&&d!=7)return false;
        x/=10;
    }
    return true;
}
int fast(int a,int b){
    int res=1;
    while(b){
        if(b&1)res=1LL*res*a%P;
        b>>=1;
        a=1LL*a*a%P;
    }
    return res;
}
int Calc(int n,int m){
    if(n>m)return 0;
    return 1LL*fact[m]*fast(fact[m-n],P-2)%P*fast(fact[n],P-2)%P;
}
void Check(int &a,int b){
    a+=b;
    if(a>P)a%=P;
}
int main(){
//  freopen("lucky.in","r",stdin);
//  freopen("lucky.out","w",stdout);
    int n,k,tot=0,ans=0,d=0;
    scanf("%d %d",&n,&k);
    for(int i=1;i<=n;i++){
        scanf("%d",&A[i]);
        if(check(A[i]))mp[A[i]]++;
        else d++;
    }
    fact[0]=1;
    for(int i=1;i<=n;i++)
        fact[i]=1LL*fact[i-1]*i%P;
    for(map<int,int>::iterator it=mp.begin();it!=mp.end();it++)
        C[++tot]=it->second;
    for(int i=0;i<=tot;i++)
        dp[i][0]=1;
    for(int i=1;i<=tot;i++)
        for(int j=1;j<=i;j++){
            Check(dp[i][j],dp[i-1][j]);
            Check(dp[i][j],1LL*dp[i-1][j-1]*C[i]%P);
        }
    for(int i=0;i<=min(tot,k);i++)
        ans=(ans+1LL*dp[tot][i]*Calc(k-i,d))%P;
    printf("%d\n",ans);
    return 0;
}