[深度学习] 自然语言处理 --- 基于Attention机制的Bi-LSTM文本分类
Peng Zhou等发表在ACL2016的一篇论文《Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification》。
论文主要介绍了在关系分类任务中应用双向LSTM神经网络模型并加入Attention机制,从而避免了传统工作中复杂的特征工程,并在该任务中取得比较优秀的效果。
一 研究背景与动机
关系抽取(分类)是自然语言处理中一个重要的任务,也即从自然语言文本中提取两个实体之间的语义关系。关系抽取属于信息抽取的一个部分。信息激增的时代,快速、准确获取关键信息的需求也日益激增,相比于传统的信息检索,信息抽取能够快速、准确提取出海量非结构化信息中的结构化知识,它也逐渐成为搜索引擎发展的方向。而关系抽取同命名实体识别、事件抽取等任务一起,都是信息抽取的一部分或者中间过程,可应用于结构化知识抽取、知识图谱构建、自动问答系统构建等。
关系抽取从本质上看是一个多分类问题,对于这样一个问题来说最重要的工作无非特征的提取和分类模型的选择。传统的方法中,大多数研究依赖于一些现有的词汇资源(例如WordNet)、NLP系统或一些手工提取的特征。这样的方法可能导致计算复杂度的增加,并且特征提取工作本身会耗费大量的时间和精力,特征提取质量的对于实验的结果也有很大的影响。因此,这篇论文从这一角度出发,提出一个基于Attention机制的双向LSTM神经网络模型进行关系抽取研究,Attention机制能够自动发现那些对于分类起到关键作用的词,使得这个模型可以从每个句子中捕获最重要的语义信息,它不依赖于任何外部的知识或者NLP系统。
二、算法模型详解
其他模型里Attention结构
Hierarchical Attention Networks for Document Classification
这篇文章主要讲述了基于Attention机制实现文本分类
假设我们有很多新闻文档,这些文档属于三类:军事、体育、娱乐。其中有一个文档D有L个句子si(i代表s是文档D的第i个句子),每个句子包含Ti个词(word),wit代表第i个句子的word,t∈[0,T]
Word Encoder:
①给定一个句子si,例如 The superstar is walking in the street,由下面表示[wi1,wi2,wi3,wi4,wi5,wi6,wi1,wi7],我们使用一个词嵌入矩阵W将单词编码为向量
Word Attention:
给定一句话,并不是这个句子中所有的单词对个句子语义起同等大小的“贡献”,比如上句话“The”,“is”等,这些词没有太大作用,因此我们需要使用attention机制来提炼那些比较重要的单词,通过赋予权重以提高他们的重要性。
①通过一个MLP获取hit的隐含表示:
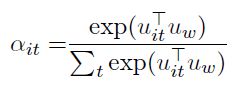
③计算句子向量:
通过每个单词获取的hit与对应权重αit乘积,然后获取获得句子向量
W与b为Attention的权重与bias,在实现的时候也要设置attention的size,不过也可以简单的令它们等于BIRNN的输出向量的size。
Uw也是需要设置的权重,公式(2)其实也就是对所有Ut*Uw结果的softmax。
Tensorflow: https://github.com/ilivans/tf-rnn-attention/blob/master/attention.py
import tensorflow as tf
def attention(inputs, attention_size, time_major=False, return_alphas=False):
"""
Attention mechanism layer which reduces RNN/Bi-RNN outputs with Attention vector.
The idea was proposed in the article by Z. Yang et al., "Hierarchical Attention Networks
for Document Classification", 2016: http://www.aclweb.org/anthology/N16-1174.
Variables notation is also inherited from the article
Args:
inputs: The Attention inputs.
Matches outputs of RNN/Bi-RNN layer (not final state):
In case of RNN, this must be RNN outputs `Tensor`:
If time_major == False (default), this must be a tensor of shape:
`[batch_size, max_time, cell.output_size]`.
If time_major == True, this must be a tensor of shape:
`[max_time, batch_size, cell.output_size]`.
In case of Bidirectional RNN, this must be a tuple (outputs_fw, outputs_bw) containing the forward and
the backward RNN outputs `Tensor`.
If time_major == False (default),
outputs_fw is a `Tensor` shaped:
`[batch_size, max_time, cell_fw.output_size]`
and outputs_bw is a `Tensor` shaped:
`[batch_size, max_time, cell_bw.output_size]`.
If time_major == True,
outputs_fw is a `Tensor` shaped:
`[max_time, batch_size, cell_fw.output_size]`
and outputs_bw is a `Tensor` shaped:
`[max_time, batch_size, cell_bw.output_size]`.
attention_size: Linear size of the Attention weights.
time_major: The shape format of the `inputs` Tensors.
If true, these `Tensors` must be shaped `[max_time, batch_size, depth]`.
If false, these `Tensors` must be shaped `[batch_size, max_time, depth]`.
Using `time_major = True` is a bit more efficient because it avoids
transposes at the beginning and end of the RNN calculation. However,
most TensorFlow data is batch-major, so by default this function
accepts input and emits output in batch-major form.
return_alphas: Whether to return attention coefficients variable along with layer's output.
Used for visualization purpose.
Returns:
The Attention output `Tensor`.
In case of RNN, this will be a `Tensor` shaped:
`[batch_size, cell.output_size]`.
In case of Bidirectional RNN, this will be a `Tensor` shaped:
`[batch_size, cell_fw.output_size + cell_bw.output_size]`.
"""
if isinstance(inputs, tuple):
# In case of Bi-RNN, concatenate the forward and the backward RNN outputs.
inputs = tf.concat(inputs, 2)
if time_major:
# (T,B,D) => (B,T,D)
inputs = tf.array_ops.transpose(inputs, [1, 0, 2])
hidden_size = inputs.shape[2].value # D value - hidden size of the RNN layer
# Trainable parameters
w_omega = tf.Variable(tf.random_normal([hidden_size, attention_size], stddev=0.1))
b_omega = tf.Variable(tf.random_normal([attention_size], stddev=0.1))
u_omega = tf.Variable(tf.random_normal([attention_size], stddev=0.1))
with tf.name_scope('v'):
# Applying fully connected layer with non-linear activation to each of the B*T timestamps;
# the shape of `v` is (B,T,D)*(D,A)=(B,T,A), where A=attention_size
v = tf.tanh(tf.tensordot(inputs, w_omega, axes=1) + b_omega)
# For each of the timestamps its vector of size A from `v` is reduced with `u` vector
vu = tf.tensordot(v, u_omega, axes=1, name='vu') # (B,T) shape
alphas = tf.nn.softmax(vu, name='alphas') # (B,T) shape
# Output of (Bi-)RNN is reduced with attention vector; the result has (B,D) shape
output = tf.reduce_sum(inputs * tf.expand_dims(alphas, -1), 1)
if not return_alphas:
return output
else:
return output, alphas
Pytorch:
class Attention(nn.Module):
def __init__(self, feature_dim, step_dim, bias=True, **kwargs):
super(Attention, self).__init__(**kwargs)
self.supports_masking = True
self.bias = bias
self.feature_dim = feature_dim
self.step_dim = step_dim
self.features_dim = 0
weight = torch.zeros(feature_dim, 1)
nn.init.kaiming_uniform_(weight)
self.weight = nn.Parameter(weight)
if bias:
self.b = nn.Parameter(torch.zeros(step_dim))
def forward(self, x, mask=None):
feature_dim = self.feature_dim
step_dim = self.step_dim
eij = torch.mm(
x.contiguous().view(-1, feature_dim),
self.weight
).view(-1, step_dim)
if self.bias:
eij = eij + self.b
eij = torch.tanh(eij)
a = torch.exp(eij)
if mask is not None:
a = a * mask
a = a / (torch.sum(a, 1, keepdim=True) + 1e-10)
weighted_input = x * torch.unsqueeze(a, -1)
return torch.sum(weighted_input, 1)
论文中模型结构
Bi-LSTM + Attention 就是在Bi-LSTM的模型上加入Attention层,在Bi-LSTM中我们会用最后一个时序的输出向量 作为特征向量,然后进行softmax分类。Attention是先计算每个时序的权重,然后将所有时序 的向量进行加权和作为特征向量,然后进行softmax分类。在实验中,加上Attention确实对结果有所提升。
- 输入层:将句子输入到模型中
- Embedding层:将每个词映射到低维空间
- LSTM层:使用双向LSTM从Embedding层获取高级特征
- Attention层:生成一个权重向量,通过与这个权重向量相乘,使每一次迭代中的词汇级的特征合并为句子级的特征。
- 输出层:将句子级的特征向量用于关系分类
embedding通常有两种处理方法,一个是静态embedding,即通过事先训练好的词向量,另一种是动态embedding,即伴随着网络一起训练;
2.1 输入层
输入层输入的是以句子为单位的样本。
2.2 Word Embeddings
对于一个给定的包含T个词的句子S: S=x1,x2,…,xT。每一个词xi都是转换为一个实数向量ei。对于S中的每一个词来说,首先存在一个词向量矩阵:Wwrd∈ℝdw|V|,其中V是一个固定大小的词汇表,dw是词向量的维度,是一个由用户自定义的超参数,Wwrd则是通过训练学习到的一个参数矩阵。使用这个词向量矩阵,可以将每个词转化为其词向量的表示: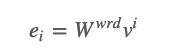 其中,vi是一个大小为|V| 的one-hot向量,在下表为ei处为1,其他位置为0。于是,句子S将被转化为一个实数矩阵:$$emb_s = {e_1, e_2, …, e_T}$,并传递给模型的下一层。
其中,vi是一个大小为|V| 的one-hot向量,在下表为ei处为1,其他位置为0。于是,句子S将被转化为一个实数矩阵:$$emb_s = {e_1, e_2, …, e_T}$,并传递给模型的下一层。
2.3 Bi-LSTM
LSTM最早由Hochreiter和Schmidhuber (1997)提出,为了解决循环神经网络中的梯度消失问题。主要思想是引入门机制,从而能够控制每一个LSTM单元保留的历史信息的程度以及记忆当前输入的信息,保留重要特征,丢弃不重要的特征。这篇论文采用了Graves等人(2013)提出的一个变体,将上一个细胞状态同时引入到输入门、遗忘门以及新信息的计算当中。对于序列建模的任务来说,每一个时刻的未来信息和历史信息同等重要,标准的LSTM模型按其顺序并不能捕获未来的信息。
因而这篇论文采用了双向LSTM模型,在原有的正向LSTM网络层上增加一层反向的LSTM层,可以表示成:hi=[h⃗ i⨁hi←]
2.4 Attention机制
由于LSTM获得每个时间点的输出信息之间的“影响程度”都是一样的,而在关系分类中,为了能够突出部分输出结果对分类的重要性,引入加权的思想,注意力机制本质上就是加权求和。
将LSTM层输入的向量集合表示为H:[h1,h2,…,hT]。其Attention层得到的权重矩阵由下面的方式得到 :
其中,H∈ℝdw×T,dw为词向量的维度,wT是一个训练学习得到的参数向量的转置。最终用以分类的句子将表示如下 :h∗=tanh(r)
Pytorch1
class GRUWithAttention(nn.Module):
def __init__(self, vocab_size, embedding_dim, n_hidden, n_out, bidirectional=False):
super().__init__()
self.vocab_size = vocab_size
self.embedding_dim = embedding_dim
self.n_hidden = n_hidden
self.n_out = n_out
self.bidirectional = bidirectional
self.emb = nn.Embedding(self.vocab_size, self.embedding_dim)
self.emb_drop = nn.Dropout(0.3)
self.gru = nn.GRU(self.embedding_dim, self.n_hidden, dropout=0.3, bidirectional=bidirectional)
# attention layer
self.attention_layer = nn.Sequential(
nn.Linear(self.n_hidden*2, self.n_hidden*2),
nn.ReLU(inplace=True)
)
if bidirectional:
self.fc = nn.Linear(self.n_hidden*2, self.n_out)
else:
self.fc = nn.Linear(self.n_hidden, self.n_out)
def forward(self, seq, lengths):
self.h = self.init_hidden(seq.size(1))
embs = self.emb_drop(self.emb(seq))
embs = pack_padded_sequence(embs, lengths)
gru_out, self.h = self.gru(embs, self.h)
gru_out, lengths = pad_packed_sequence(gru_out)
gru_out = gru_out.permute(1, 0, 2)
attention_out = self.attention(gru_out)
outp = self.fc(attention_out)
return F.log_softmax(outp, dim=-1) # it will return log of softmax
def init_hidden(self, batch_size):
# initialized to zero, for hidden state and cell state of LSTM
number = 1
if self.bidirectional:
number = 2
return torch.zeros((number, batch_size, self.n_hidden), requires_grad=True).to(device)
def attention(self, h):
m = nn.Tanh()(h)
# [batch_size, time_step, hidden_dims]
w = self.attention_layer(h)
# [batch_size, time_step, time_step]
alpha = F.softmax(torch.bmm(m, w.transpose(1, 2)), dim=-1)
context = torch.bmm(h.transpose(1,2), alpha)
result = nn.Tanh()(torch.sum(context, dim=-1))
return result
Pytorch2
class GRUWithAttention2(nn.Module):
def __init__(self, vocab_size, embedding_dim, n_hidden, n_out, bidirectional=False):
super().__init__()
self.vocab_size = vocab_size
self.embedding_dim = embedding_dim
self.n_hidden = n_hidden
self.n_out = n_out
self.bidirectional = bidirectional
self.emb = nn.Embedding(self.vocab_size, self.embedding_dim)
self.emb_drop = nn.Dropout(0.3)
self.gru = nn.GRU(self.embedding_dim, self.n_hidden, dropout=0.3, bidirectional=bidirectional)
weight = torch.zeros(1, self.n_hidden*2)
nn.init.kaiming_uniform_(weight)
self.attention_weights = nn.Parameter(weight)
if bidirectional:
self.fc = nn.Linear(self.n_hidden*2, self.n_out)
else:
self.fc = nn.Linear(self.n_hidden, self.n_out)
def forward(self, seq, lengths):
self.h = self.init_hidden(seq.size(1))
embs = self.emb_drop(self.emb(seq))
embs = pack_padded_sequence(embs, lengths)
gru_out, self.h = self.gru(embs, self.h)
gru_out, lengths = pad_packed_sequence(gru_out)
gru_out = gru_out.permute(1, 0, 2)
attention_out = self.attention(gru_out)
outp = self.fc(attention_out)
return F.log_softmax(outp, dim=-1) # it will return log of softmax
def init_hidden(self, batch_size):
# initialized to zero, for hidden state and cell state of LSTM
number = 1
if self.bidirectional:
number = 2
return torch.zeros((number, batch_size, self.n_hidden), requires_grad=True).to(device)
def attention(self, h):
batch_size = h.size()[0]
m = F.tanh(h)
# apply attention layer
hw = torch.bmm(m, # (batch_size, time_step, hidden_size*2)
self.attention_weights # (1, hidden_size*2)
.permute(1, 0) # (hidden_size, 1)
.unsqueeze(0) # (1, hidden_size, 1)
.repeat(batch_size, 1, 1) # (batch_size, hidden_size*2, 1)
)
alpha = F.softmax(hw, dim=-1)
context = torch.bmm(h.transpose(1,2), alpha)
result = F.tanh(torch.sum(context, dim=-1))
return result
Tensorflow参考
def attention(self, H):
"""
利用Attention机制得到句子的向量表示
"""
# 对Bi-LSTM的输出用激活函数做非线性转换
M = tf.tanh(H)
# 获得最后一层LSTM的神经元数量
hiddenSize = config.model.hiddenSizes[-1]
# 初始化一个权重向量,是可训练的参数
W = tf.Variable(tf.random_normal([hiddenSize], stddev=0.1))
# 对W和M做矩阵运算,W=[batch_size, time_step, hidden_size],计算前做维度转换成[batch_size * time_step, hidden_size]
# newM = [batch_size, time_step, 1],每一个时间步的输出由向量转换成一个数字
newM = tf.matmul(tf.reshape(M, [-1, hiddenSize]), tf.reshape(W, [-1, 1]))
# 对newM做维度转换成[batch_size, time_step]
restoreM = tf.reshape(newM, [-1, config.sequenceLength])
# 用softmax做归一化处理[batch_size, time_step]
self.alpha = tf.nn.softmax(restoreM)
# 利用求得的alpha的值对H进行加权求和,用矩阵运算直接操作
r = tf.matmul(tf.transpose(H, [0, 2, 1]), tf.reshape(self.alpha, [-1, config.sequenceLength, 1]))
# 将三维压缩成二维sequeezeR=[batch_size, hidden_size]
sequeezeR = tf.reshape(r, [-1, hiddenSize])
sentenceRepren = tf.tanh(sequeezeR)
# 对Attention的输出可以做dropout处理
output = tf.nn.dropout(sentenceRepren, self.dropoutKeepProb)
return output
2.5 损失函数
分类使用一个softmax分类器来预测标签ŷ 。该分类器将上一层得到的隐状态作为输入:
其中t∈ℜm为正样本的one-hot表示,y∈ℜm为softmax估计出的每个类别的概率(m为类别个数),λ是L2正则化的超参数。这篇论文中使用了Dropout和L2正则化的组合以减轻过拟合的情况 。
![[深度学习] 自然语言处理 --- 基于Attention机制的Bi-LSTM文本分类_第1张图片](http://img.e-com-net.com/image/info8/1f74e32f0be74cc59d7dbe9aa2273cb4.jpg)
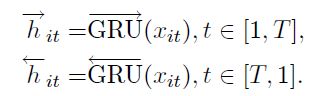

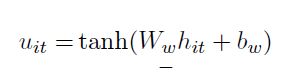
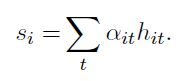
![[深度学习] 自然语言处理 --- 基于Attention机制的Bi-LSTM文本分类_第2张图片](http://img.e-com-net.com/image/info8/661c2293bbad4a53833bbda79a078a2d.jpg)
![[深度学习] 自然语言处理 --- 基于Attention机制的Bi-LSTM文本分类_第3张图片](http://img.e-com-net.com/image/info8/4022767302d94d46a3cc4c4df9740a22.jpg)
![[深度学习] 自然语言处理 --- 基于Attention机制的Bi-LSTM文本分类_第4张图片](http://img.e-com-net.com/image/info8/59be438c3d4d4306868b09166c3f1ea5.jpg)
![[深度学习] 自然语言处理 --- 基于Attention机制的Bi-LSTM文本分类_第5张图片](http://img.e-com-net.com/image/info8/6de0e220d45b413eb8c86b431d1400c1.jpg)
