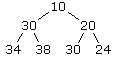在A*路径规划算法中使用二叉堆
A*路径规划算法中最慢的一部分就是在open列表中寻找具有最小耗费F值的那个节点。依照你的地图的大小而定,可能会有几十,上百甚至上千个节点,在你使用A*算法时需要不断的进行搜索。毫无疑问,在这么大的列表中重复的进行搜索会严重降低效率。我们如何保存open列表中的数据项对最终我们查找所需的时间有很大影响。
排序或不排序Open列表:一个简单方法
一种简单的处理Open列表的方法是存储每一个需要的节点,然后当你需要的时候,遍历整个列表找出具有最小耗费的项目。这样插入方式可能是最快的,但是删除可能会是最慢的,因为你需要检查列表中的每一个节点并确保选择的那个的F值是最小的。
你可以通过保持你的列表有序来大大提高效率。这可能需要些预处理工作,因为每次你添加新项目到列表中时,你需要将它插入到合适的位置。但是删除节点是很快的。你只需要拿出列表中第一个节点,因为有序,它就是那个具有最小F值的节点。
保证数据有序有好多种方法(选择排序,冒泡排序,快排等),并且你可以很容易用你最喜欢的搜索引擎搜索到这些方法的具体内容。但是这里我们有一些别的想法。一个最简单的方法是当你加入一个新节点时,你需要从列表的头开始,与你已经加入的所有节点的F值进行比较。当你找到一个节点的F值大于或等于这个节点时,你就可以将我们要插入的那个节点插入到找到的这个节点的前面。依据你使用的语言,使用类或结构体实现链表可能是一个比较好的方法。
这个过程我们可以进行改进,通过记录整个列表中的节点的F耗费的平均值,我们可以决定在插入新节点的时候是从起始开始,还是从末尾开始。也就是,当插入的新节点比平均值F小的话,我们从列表的起始点开始向后查找,如果比平均值大,我们从列表的尾节点开始向前查找。这个方法可以将你的查找时间减半。
二叉堆
二叉堆与刚才我们所描写的快排方法很相近,同时也被许多想保证他们的A*算法尽可能快的人使用。根据我的经验,利用二叉堆可以平均提高路径搜索效率2-3被,对于具有许多节点的大地图(指具有100*100节点或更多),效率提高的更多。但是不管怎么样,公正的说,二叉堆是比较复杂的,如果地图不是有太多节点并且速度要求没有那么严格,我们大可不必去费那脑细胞来弄个二叉堆。
文章的余下部分将讲解二叉堆和如何在A*中使用。
仍然感兴趣么?好的,我们开始吧……
在有序列表中,所有列表中的节点都具有正确的次序,由低到高,由高到低。这很有帮助,但实际上,这远超我们所需了。我们实际上不需要关心在列表上127是否比128小。我们所需要的仅仅可以容易的从列表头处获得那个F值最小的节点。列表的其他部分是杂乱的也没关系。保持其他的节点有序仅仅是额外的不需要的工作。当然,我们需要下一个最小的F值节点。
基本上,我们真正需要的,仅仅是一个叫做堆的东西,或者更准确点是二叉堆。二叉堆是一系列节点并且满足最小或最大值(看你的需求)的那个节点在堆的最顶端。由于我们要找具有最小F值的节点,所以我们需要将这个具有最小值的节点放在堆顶。这个节点有两个子节点,每一个的F值都大于或等于父节点的F值。并且每一个子节点也具有自己的子节点,并且同样满足它们的F值不大于子节点的F值。下面就是一个堆的例子:
可以看到列表中的最小值10在最顶端,第二小的值是它的孩子节点。然而世事难料,在这个二叉堆中,列表中第三小的节点是24,它距离顶端两层,但是比他大的30却位于距离堆顶只有一层左侧。简言之,对于堆中的其他节点来说这都没关系,只要每个节点满足不小于它的父亲节点,并且不大于它的孩子节点就行。这些条件都满足,那它就是一个严格的二叉堆。
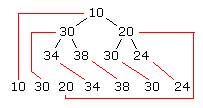
好吧,到现在你可能会认为这还是比较有趣的,但是如何实际在不同情景中使用它呢?一个非常有趣的事就是你可以用非常简单的一维数组来保存一个堆。在这个数组中,堆顶元素位于数组的第一个位置(索引为1,而不是0)。它的两个孩子位于2和3。这两个子节点的孩子节点的位置是4-7。
一般的,堆中任何节点的两个孩子都能在数组中通过对当前节点的位置乘2(找到第一个孩子节点),或者乘2再加上1(找到第二个孩子节点)找到。例如第三个节点(值为20)的两个孩子节点,2*3=6,找到30,2*3+1=7,找到24。
你不用非得知道这一点,但是这里提出来是非常值得的,那就是对不允许有洞。就是说,如果有7个节点,那么它必须排满三层的每一行。但这并不是必须的。为了使我们的堆是一个有效的堆,我们至少要保证在最底层以上的每一行都是满的。在最底层我们可以有任意数量的节点。但是新节点在最底层是需要从左向右进行添加的。
向堆中添加节点
在利用堆进行路径规划之前我们还需要考虑一些东西,但是现在我们先学习使用二叉堆的一些基本要素。我建议你简单的读一下这部分来了解一下堆的基本要素。在文章后面我会给你一个公式可以帮你处理一切。但是理解一些基本的东西还是比较需要的。
一般,要加入一个节点到堆,我们先把它放在数组最末尾。然后与它的父节点比较,位置是当前节点位置/2(舍去未除尽的小数)。如果新节点的F值更小,那么交换这两个节点。接下来我们将这个节点与它的新父节点比较。如果它的F值更小,那么在此交换。重复这个过程,直到这个节点的F值不小于父节点,或者这个节点最终上升到顶点,位于数组中索引为1的位置。
举例说明,我们想将一个F值为17的点加入到当前堆中。我们已经有7个点在堆中,那么这个节点将被放在位置8,下面是堆的样子,带下划线的是新节点
10 30 20 34 38 30 24 17
接下来我们将这个节点与它的父节点比较,位置是8/2=4。F值是34.由于17比34小,所以交换它们。堆变成下面样子:
10 30 20 17 38 30 24 34
然后我们将这个节点跟它的新节点比较。由于我们的位置现在变成了4,那么父节点的位置是4/2=2。这个节点的F值是30.17小于30,同样交换它们。堆变成:
10 17 20 30 38 30 24 34
我们继续将它和新父节点比较。由于当前位置是2,父节点位置是2/2=1,堆的头节点,由于17大于10,所以停止比较。
从堆中删除节点
从堆中删除节点是一个相似的过程,是某种程度上的反向过程。首先我们移除堆顶元素,然后将堆中最后的节点移到位置1上来,这一步后堆的样子如下,带下划线的是我们移上来的节点
34 17 20 30 38 30 24
接下来我们将它和它的子节点比较,它们的位置分别是当前的位置*2和当前位置*2+1。如果它比任何一个子节点的F值都小,那么这就是它的最终位置。如果不是,那么交换它和F值最小的子节点。我们这个例子中,子节点分别是位于1*2=2和1*2+1=3的两个节点。由于34不小于任何一个子节点,所以将它与最小的那个子节点进行交换,也就是17.交换后如下:
17 34 20 30 38 30 24
接下来我们将这个节点与它的新子节点进行比较,位置分别是2*2=4和2*2+1=5.同样它并不是比每个节点的值都小,那么将它与具有最小值的节点交换,也就是位于位置4的30.然后效果如下:
17 30 20 34 38 30 24
最终我们依然比较它与它的子节点。节点位置分别是8和9.但是由于不存在这两个位置的节点,我们的堆没那么大。我们已经到了堆的最底层,所以我们停止比较。
为什么二叉堆这么快?
现在了解了从堆中插入和删除的基本概念,那么你将会明白为什么它比其他排序例如插入排序,要快那么多。假象一下,如果你有一个具有1000个节点的开放列表(虽然对于一个一般大小的地图来说仅有这么点不太可能,记住仅仅一个100*100的地图就有10,000个节点之多)。如果你用一个简单的插入排序的话,从列表的头开始处理,知道你找到一个合适的插入位置。在你插入之前你平均需要做500比较才可以。
使用二叉堆的话,如果从底部开始你仅仅平均需要比较1-3次就能插入到正确的位置。你仅仅平均需要比较9次就可以删除一个节点并且重新是的堆有序。在A*中,你通常需要在每一个路径点都删除一个节点(F值最小的那个节点),同时添加0到5个新节点(是用2D方法表示)。同样数量的节点,利用二叉堆能够将时间消耗减少到插入排序的1%。如果你的地图更大,那么效率会成几何数级增长。但是对于小地图来说,可能获得的好处并不会太多。
顺便说一下,尽管你在路径规划中使用了二叉堆,这并不意味着你的速度就会提升100倍。因为它同样会有一些额外的消耗,下面我将会描述。另外对于A*来说除了对Open列表进行排序外,它还有许多工作要做。但是以我的经验,使用了二叉堆会是你的算法在大多数情况下要快2-3倍,对于更大的路径来说可能要更快。
创建Open列表数组
现在我们知道什么是二叉堆,那么如何使用呢?我们要做的第一件事就是正确的定义我们需要的一维数组。我们首先要做的就是要确定它会有多大。一般,列表不可能比地图中的所有节点数还大(加入最坏情况下,我们查询了整个地图)。在一个二维地图中,不可能有大于mapWidth*mapHeight个节点。所以我们的数组就应该那么大。在我们的例子中,我们把这个数组叫做openList()。堆顶应该存储在openList(1),第二个节点存储在openList(2),依此类推。
使用指针
现在我们有了一个合适大小的一维数组,我们已经准备好了使用它来进行路径规划。在我们继续深入之前,让我们再看看原始的堆。
目前,我们仅仅有了一个F值的列表,并被正确的排列。但是我们忽略了一个重要的元素。尽管,我们有了一些以二叉堆的顺序排列好的F值,但是我们不知道具有F值的点对应的是地图中的哪一块。
也就是说,我们现在所知道的只是F值为10的那个点是堆中F值最小的点。但是并不知道它是地图方块中的哪一个。
为了解决这个问题,我们应该修改数组中元素的值。与在数组中存储F值不同,我们需要存储一个唯一的标识号码来告诉我们它到底是地图中的哪一块。我的方法是在向堆中加入新的节点的时候都创建一个唯一的ID,叫做squaresChecked。每次我们加入一个新的节点到开放列表中,我们都给squaresChecked自增,并使用这个ID将新节点加入到开放列表。那么第一个加入到开放列表中的节点号是1,第二个是2,然后依次类推。
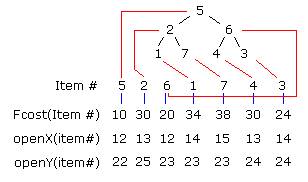
最后,我们需要保存每一个块的实际的F值到一个单独的数组中,通过调用Fcost()方法。同样我会通过调用openX()和openY来保存地图上节点的x和y坐标到另外的数组中。最终视觉上,总体的效果如下:
当然这看起来似乎有点复杂,但它同样是之前我们举例的那个堆。我们只是加入了一些新的信息而已。
项目#5,具有最小的Fcost 10,仍然位于堆的最顶端。但是我们现在堆中存储的是它的唯一标示ID 5,而不是F值。意思就是openList(1)=5。这个唯一标示接下来会用于查询它对应节点的F值和位于地图中的x,y坐标。它的Fcost是Fcost(5)=10,然后x和y坐标分别是openX(5)=12和openY(5)=22.
实际上,我们的堆与之前的堆并无差异,仅仅是具有了更多的信息而已,比如节点在地图中的位置以及它对应的F值。
加入一个新节点到堆中(部分2)
好的,接下来让我们将这个技术应用到open列表的排序中使得A*路径规划算法可用。
我们加入到open列表中的第一项实际上就是起始节点。它被指定了一个唯一标示ID,1。然后放到open列表的第一个位置,即openList(1)=1.我们需要跟踪我们加入到open列表中的节点,现在也就是1这个节点。我们将它先保存到一个叫做callednumberOfOpenListItems的变量中。
然后我们向open列表中加入新的节点,首先先计算出它们的G,H,F的值。然后我们将它们加入到二叉堆中。每次我们通过使用squaresChecked 这个参数给新加的节点指定一个ID号。每次添加新节点到开放列表中时,都给这个变量加1。然后给numberOfOpenListItems 加1。然后将其放在open列表中的最底下。如下:
squaresChecked = squaresChecked +1
numberOfOpenListItems = numberOfOpenListItems+1
openList(numberOfOpenListItems) = squaresChecked
然后我们不断的将它与父节点进行比较,知道它找到一个在堆中的合适的位置。下面是实现的一些代码:
m = numberOfOpenListItems
While m <> 1 ;
While 节点没有上升到堆顶 (m=1);
if child <= parent.
If so, swap them.
If Fcost(openList(m)) <= Fcost(openList(m/2)) Then
temp = openList(m/2)
openList(m/2) = openList(m)
openList(m) = temp
m = m/2
Else
Exit ;exit the while/wend loop
End If
Wend
从堆中删除节点(部分2)
当然我们不仅仅只需要建立一个堆,我们还需要从堆中删除不需要的节点。一般,A*算法需要对我们已经处理过并将它放进closed列表中的那个F值最小的节点从堆顶删除。
正向我们文章前面所讲,你需要将堆中最后面的那个节点移到最前面来,然后给节点数减一。伪代码如下:
openList(1) = openList(numberOfOpenListItems)
numberOfOpenListItems = numberOfOpenListItems - 1
接下来我们不断的将这个节点的F值和它的子节点比较。如果大于任何一个子节点,我们就将它与最小的那个子节点进行交换。然后我们继续将其与它的新子节点比较,如果仍然比子节点的值大,那么继续交换,重复这个过程直到找到一个合适的位置。下面是伪代码:
v = 1;
重复下面的操作,直到节点下沉到二叉堆中合适的位置
Repeat
u = v
If 2*u+1 <= numberOfOpenListItems ;
if both children exist
Select the lowest of the two children.
If Fcost(openList(u)) >= Fcost(openList(2*u))then v = 2*u ;SEE NOTE BELOW
If Fcost(openList(v)) >= Fcost(openList(2*u+1))then v = 2*u+1 ;SEE NOTE BELOW
Else If 2*u <= numberOfOpenListItems ;if only child #1 exists
;Check if the F cost is greater than the child
If Fcost(openList(u)) >= Fcost(openList(2*u))then v = 2*u
End If
If u <> v then ; If parent's F > one or both of its children, swap them
temp = openList(u)
openList(u) = openList(v)
openList(v) = temp
Else
Exit ;if item <= both children, exit repeat/forever loop
End if
请注意红色加粗的关于u,v的那两行代码,在第二行,你使用的是v,而不是u,你可能不会一眼就看出是为什么。这样的做法是确保交换的最终结果是,这个节点是和两个子节点中F值最小的那个交换的。如果没这样做的话,你可能得到的不是一个正确的堆,那么你的路径规划就不会是正确的。
重新对当前Open列表里的节点排序
根据A*算法,我们知道,有时候Open列表里的节点的F值可能被改变。当这种情况发生时,你不需要把它删除,然后整个重新调整。仅需要在它当前位置,使用它的新F值与父节点进行比较。如果它的F值的确比父节点的小,那么你就需要重新调整了,否则堆会被破坏。一般情况下,你需要使用刚才所讲的“添加节点到堆”中的相同的代码。
最终总结
好吧,我希望你一直读到这时,不会再糊涂。如果你想自己构建一个使用二叉堆的路径规划算法,那么我有一些建议:
第一,先不考虑二叉堆,而是集中精力使用一般的排序方法将你的A*算法搞对,没有bug。一开始你并不需要是它运行有多快,你只需要确保它运行正确。
第二,在你添加二叉堆代码之前,先单独做一个你想要的二叉堆功能,并将它测试通过。
当你确信你的这两个程序都运行正确时,备份一下这两份程序,然后试着将他们放在一起。除非你比我聪明的多,否则,一开始你一定会遇到问题。仔细调试,最终你一定会使他成功运行的。