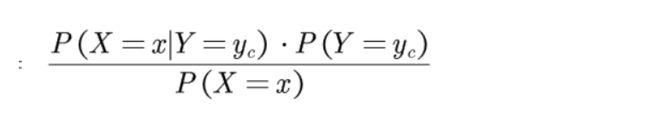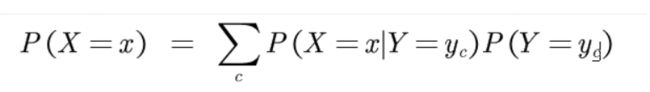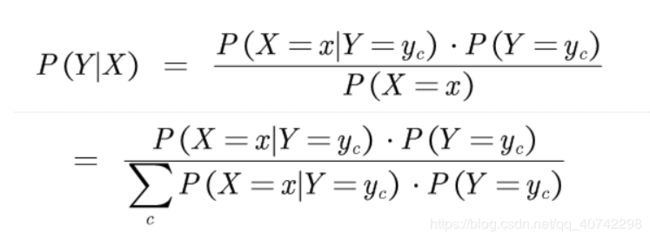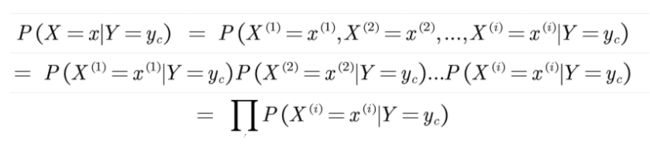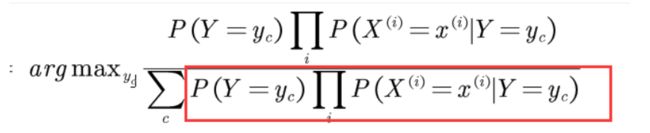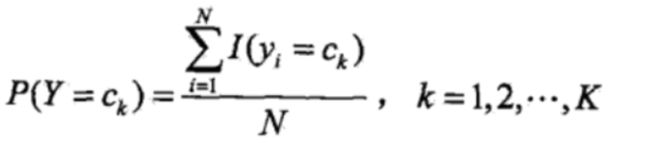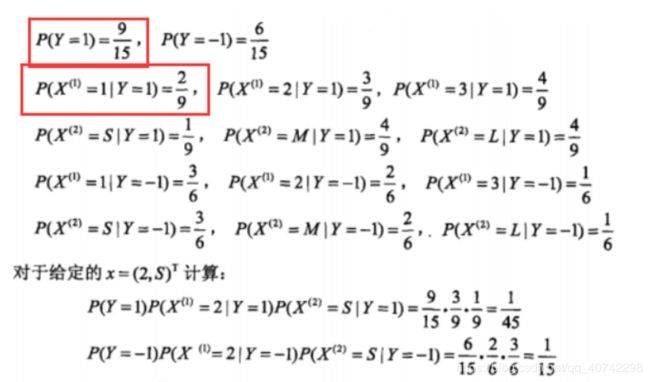朴素贝叶斯 latex手打公式 良心推导 原理分析 个人理解
文章目录
- 简介
- 怎么计算P(Y|X)
- 怎么计算P(X=x|Y=yc)
- 得到最终的判别公式
- 判别公式优化
- 求解P(Y = yc)
- 求解P(X^(i)=x^(i)|Y=yc)
- 例题分析
- 朴素贝叶斯算法总结:
- 朴素贝叶斯 和 贝叶斯
- 总结
简介
我认为朴素贝叶斯的真正灵魂就是概率。
先请大家看一个有趣的概率问题:三门问题
有趣的概率 三门问题
可能有的有点远了,哈哈,再看一个真实的OCR例子吧。
现在有10个首先的训练集数据,从0到9的手写数字图片。然后现在输入一个数字Y,那么请问这个数字是几呢?
朴素贝叶斯老师会怎么做嘞?
他会计算P(Y = 0|X), P(Y = 1|X) …,P(Y = 9|X),然后输出一个最大的,就是结果了。
怎么计算P(Y|X)
他来了,他来了!
我们现在用一个简单地例子
疫情期间我们需要对一个人是否感染进行预测,y = 0(没有感染),y = 1(感染)
观察的特征是X,其中包括X(1),特征一(比如:抗体含量);X(2)(比如:肺部某某指标)…
然后我们需要利用朴素贝叶斯原理建立一个分类器,得到是否感染。
注:只是举一个例子哈,别当真,帮助理解
计算P(Y|X)下面这个公式一定要理解,我认为他是朴素贝叶斯的灵魂:
其中我相信大家都知道第一个推导的意思,我们还是详细的解释一下,对于:
- P(Y=yc):样本中感染(未感染)的样本所占的概率
- P(X=x|Y=yc):在给定患者是否感染的情况下,其中具有x特征表现得样本的占比(概率)
- P(X=x):这个似乎还不是很明确,我们来看看
好的我们回到计算P(Y|X)中,现在我们已经完全理解了这个计算公式:
怎么计算P(X=x|Y=yc)
我一开始觉得P(X|Y)简直太好算了,但是实际操作的时候我就发现和我想的不一样,因为一个特征向量x有很多特征(x(1),x(2)…x^(n)),这时候我们需要怎么计算呢。
我用latex进行了推导,绝对良心推导:
这里将每一个特征都单独计算了,那么这样计算的前提就是每个特征都是独立的。比如P(AB)只有当AB独立的时候才能等于P(A)*P(B)。
那么朴素贝叶斯为什么可以直接拆开呢,这是因为大家如果看过一些官方教材的话,肯定会看到条件独立性假设。也就是说如果你使用了朴素贝叶斯,好的那就说明你已经默认了条件独立性。
不过我也觉得有些牵强,因为虽然这样假设计算会变得简单但是事实上特征之间不独立的可能性是很高的。大多数时候都是具有相关性的。用我们开始举得例子,如果你的肺部特征显示发炎,那么和你的血液抗体水平肯定是具有一些相关性的。
不过如果我们将各特征的相关性考虑在建模当中的话就会造成非常庞大、复杂的模型,面对简单地模型还能有比较好的表现,毫无疑问我们就闭着眼睛选择不管那些复杂的东西吗。就认为特征是独立的吧。
猜测:不知道数学家怎么看待我们这么不严谨地使用朴素贝叶斯原理,哈哈哈
分割线
得到最终的判别公式
由上述推导可知:
解释:
求解当概率最大时的yc,是哪个类别。
现在得到上述公式,我们离最终的答案已经很近了,呼~ 沉住气。
判别公式优化
因为我们可以知道无论yc怎么变化分母整体的大小其实是不变的:
因为他是所有的类别连乘,所以可以对公式进行简化,得到:
求解P(Y = yc)
来吧,最后阶段了:
这里我们使用李老师原著的图:
其中:
- N:样本总数
- I:理解为sign,就是得到的是1或者0(分别表示y=yc、y<>yc),我和李老师用的符号不太一样,大家注意一下,别出现歧义
有没有发现超级简单。
求解P(X(i)=x(i)|Y=yc)
上书中原图:
我知道你现在这个式子应该看得有点一知半解,我们来个例题,保证立马就会朴素贝叶斯。
例题分析
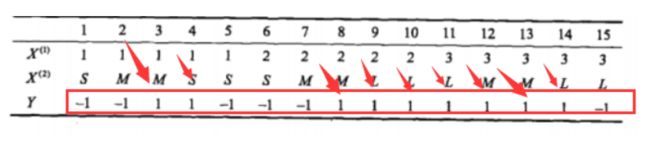
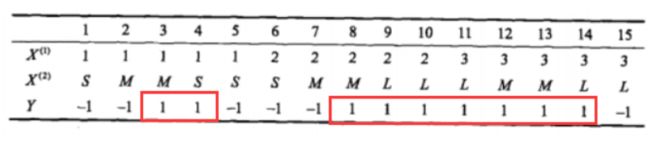
还是书中的原题:
我们分析下图中红框中的一些计算过程:
- 计算P(Y=1):
一共N = 15,然后标剪头的就是Y=1的,一共有9个,所以P(Y=1)=9/15
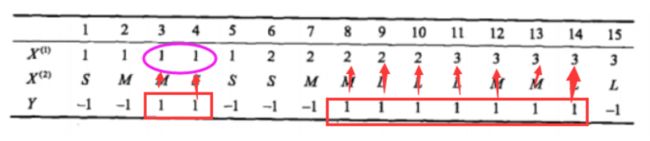
- 计算P(X^(i)=1|Y=1)
首先分母就是Y=1的样本数,
所以分母是9
然后分子就是在Y = 1的样本中,X^(1)是1的样本数:
所以P(X^(i)=1|Y=1)=2/9
其他的就可以根据我们上面的公式进行计算。
朴素贝叶斯算法总结:
摘自李老师书中:
朴素贝叶斯 和 贝叶斯
大家可以看这篇博客,我觉得还是挺重要的,尤其是在应用的时候:
难道朴素贝叶斯比贝叶斯朴素?
总结
朴素贝叶斯模型是非常重要和基础的基于概率的分类模型,简单和快速是它最大的优点。在实际的应用中面对一些复杂的问题也能有比较好的表现。
注:实际应用中的两个问题
- 保证概率项不能为0,具体请见链接
难道朴素贝叶斯比贝叶斯朴素?
- 高维特征导致的下溢出
什么意思呢?
比如一个数据集,维度超过1000维,这很常见,那么也就是说会有1000个概率相乘,哇哦。
结果我想你也想到了,那就是得到的结果贼小,一个不小心就会造成程序错误。
所以我们要进行log或者是反归一化,对概率连乘进行log或者反归一(MinMaxScale)。
就这样吧,欢迎大家指正。
大家共勉~