【学点数据结构和算法】06-二叉堆和优先队列
写在前面: 博主是一名软件工程系大数据应用开发专业大二的学生,昵称来源于《爱丽丝梦游仙境》中的Alice和自己的昵称。作为一名互联网小白,
写博客一方面是为了记录自己的学习历程,一方面是希望能够帮助到很多和自己一样处于起步阶段的萌新。由于水平有限,博客中难免会有一些错误,有纰漏之处恳请各位大佬不吝赐教!个人小站:http://alices.ibilibili.xyz/ , 博客主页:https://alice.blog.csdn.net/
尽管当前水平可能不及各位大佬,但我还是希望自己能够做得更好,因为一天的生活就是一生的缩影。我希望在最美的年华,做最好的自己!
上一篇博客《【学点数据结构和算法】05-树》借助《小灰算法》为初入数据结构大门的朋友们带来了一场视觉盛宴。本篇,要介绍的二叉堆,同样是一种基础数据结构,但它也是一种特殊的二叉树。具体是怎么一回事呢?让我们继续往下看!
文章目录
- 1、初识二叉堆
- 2、二叉堆的自我调整
- 2.1 插入节点
- 2.2 删除节点
- 2.3 构建二叉堆
- 2.4 二叉堆的代码实现
- 2.5 二叉堆的作用
- 3、优先队列
- 3.1 优先队列的实现
- 3.2 优先队列的代码
- 小结
1、初识二叉堆
二叉堆本质上是一种完全二叉树,它分为两个类型。
- 最大堆
- 最小堆
什么是最大堆呢?最大堆的任何一个父节点的值,都大于或等于它左、右孩子节点 的值。

什么是最小堆呢?最小堆的任何一个父节点的值,都小于或等于它左、右孩子节点的值。
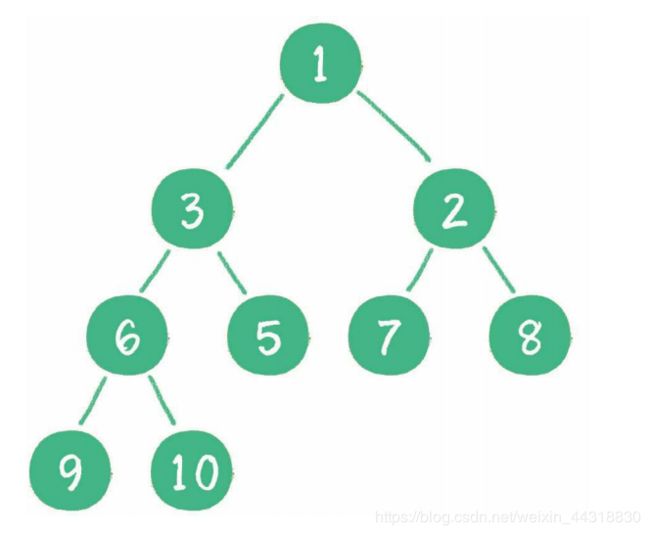
二叉堆的根节点叫作堆顶。
最大堆和最小堆的特点决定了:最大堆的堆顶是整个堆中的最大元素;最小堆的堆
顶是整个堆中的最小元素
2、二叉堆的自我调整
对于二叉堆,有如下几种操作。
- 插入节点。
- 删除节点。
- 构建二叉堆。
这几种操作都基于堆的自我调整。所谓堆的自我调整,就是把一个不符合堆性质的完全二叉树,调整成一个堆。下面让我们以最小堆为例,看一看二叉堆是如何进行自我调整的。
2.1 插入节点
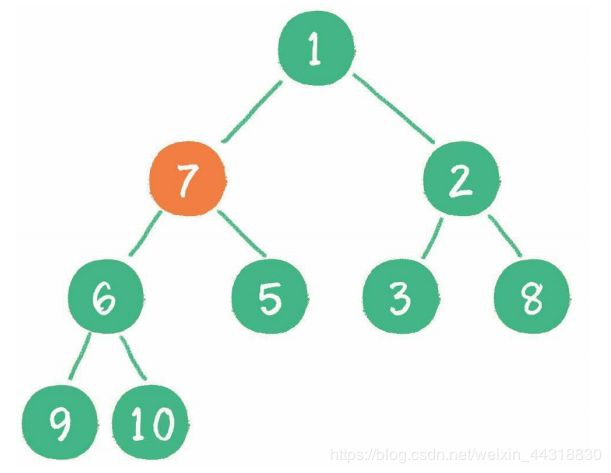
当二叉堆插入节点时,插入位置是完全二叉树的最后一个位置。例如插入一个新节 点,值是 0。
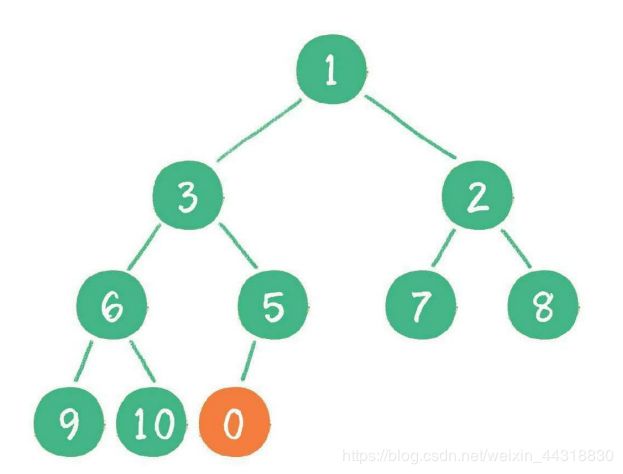
这时,新节点的父节点5比0大,显然不符合最小堆的性质。于是让新节点“上浮”,和 父节点交换位置。

继续用节点0和父节点3做比较,因为0小于3,则让新节点继续“上浮”。

继续比较,最终新节点0“上浮”到了堆顶位置。

2.2 删除节点
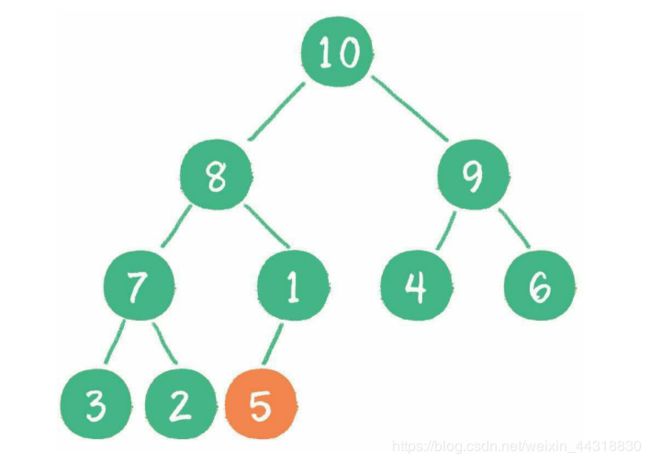
二叉堆删除节点的过程和插入节点的过程正好相反,所删除的是处于堆顶的节点。例 如删除最小堆的堆顶节点1。

这时,为了继续维持完全二叉树的结构,我们把堆的最后一个节点10临时补到原本堆 顶的位置。

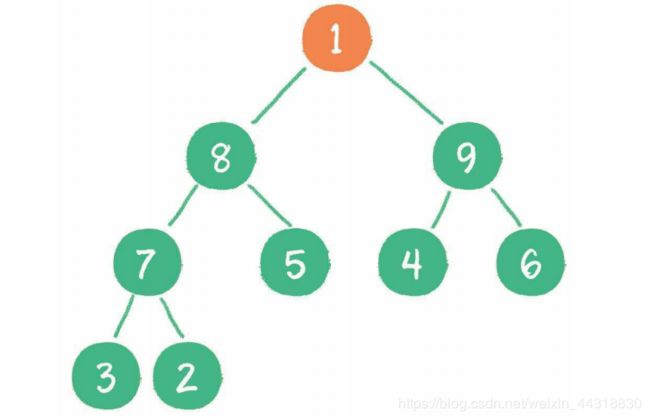
接下来,让暂处堆顶位置的节点10和它的左、右孩子进行比较,如果左、右孩子节点 中最小的一个(显然是节点2)比节点10小,那么让节点10“下沉”。

继续让节点10和它的左、右孩子做比较,左、右孩子中最小的是节点7,由于10大于 7,让节点10继续“下沉”。

这样一来,二叉堆重新得到了调整。
2.3 构建二叉堆
构建二叉堆,也就是把一个无序的完全二叉树调整为二叉堆,本质就是让所有非叶子节点依次“下沉”。
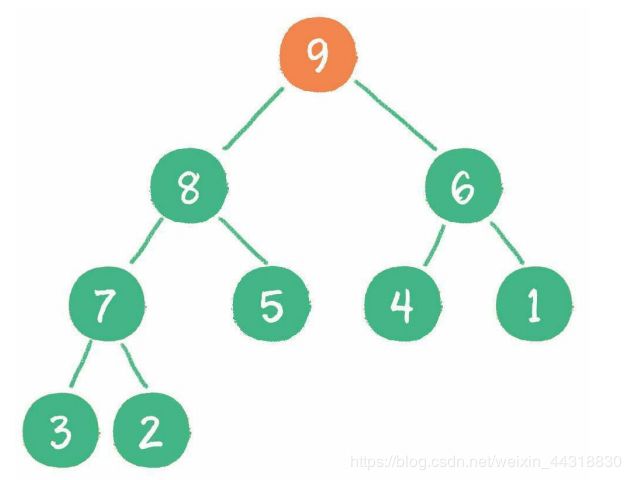
下面举一个无序完全二叉树的例子,如下图所示。
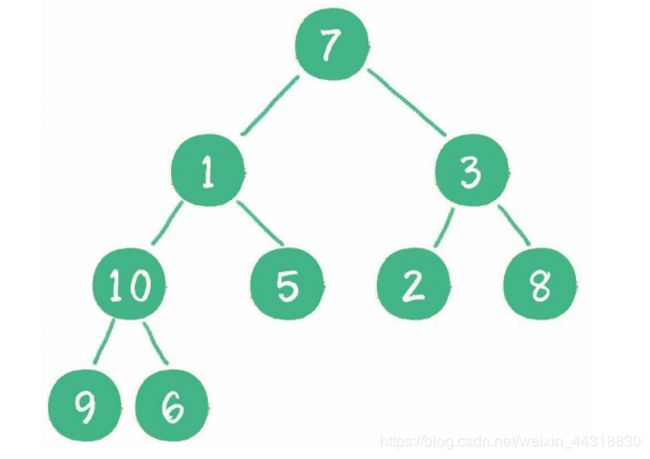
首先,从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它左、右 孩子节点中最小的一个,则节点10“下沉”。

接下来轮到节点3,如果节点3大于它左、右孩子节点中最小的一个,则节点3“下 沉”。
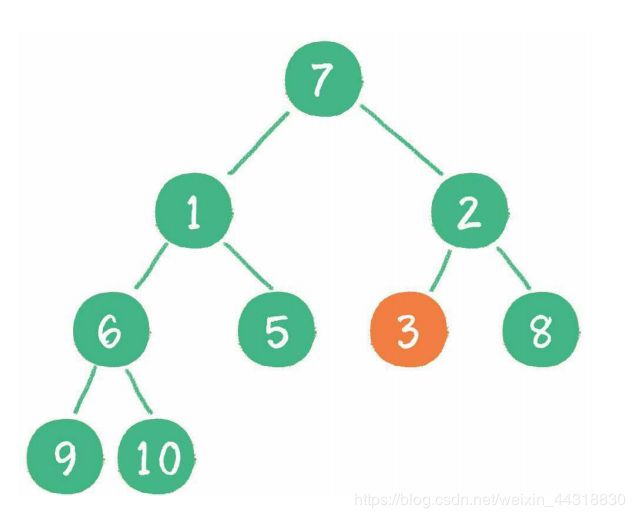
然后轮到节点1,如果节点1大于它左、右孩子节点中最小的一个,则节点1“下沉”。 事实上节点1小于它的左、右孩子,所以不用改变。
接下来轮到节点7,如果节点7大于它左、右孩子节点中最小的一个,则节点7“下 沉”。

经过上述几轮比较和“下沉”操作,最终每一节点都小于它的左、右孩子节点,一个无序的完全二叉树就被构建成了一个最小堆。
堆的插入和删除操作,时间复杂度是O(logn),但构建堆的时间复杂度是O(n)
2.4 二叉堆的代码实现
在展示代码之前,我们还需要明确一点:二叉堆虽然是一个完全二叉树,但它的存储 方式并不是链式存储,而是顺序存储。换句话说,二叉堆的所有节点都存储在数组中。
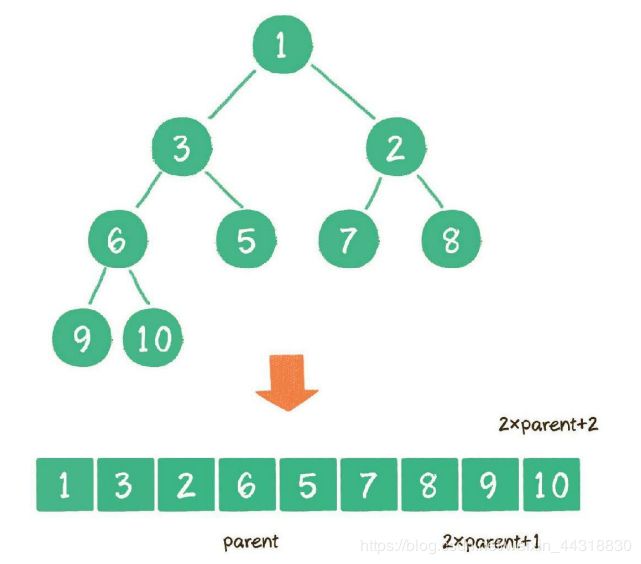
在数组中,在没有左、右指针的情况下,如何定位一个父节点的左孩子和右孩子呢?
像上图那样,可以依靠数组下标来计算。
假设父节点的下标是parent,那么它的左孩子下标就是 2×parent+1;右孩子下标就 是2×parent+2。
例如上面的例子中,节点6包含9和10两个孩子节点,节点6在数组中的下标是3,节点 9在数组中的下标是7,节点10在数组中的下标是8。
有了这个前提,下面的代码就更好理解了。
import java.util.Arrays;
public class HeapOperator {
/**
* 上浮调整
* @param array 待调整的堆
*/
public static void upAdjust(int[] array) {
int childIndex = array.length-1;
int parentIndex = (childIndex-1)/2;
// temp保存插入的叶子节点值,用于最后的赋值
int temp = array[childIndex];
while (childIndex > 0 && temp < array[parentIndex])
{
//无需真正交换,单向赋值即可
array[childIndex] = array[parentIndex];
childIndex = parentIndex;
parentIndex = (parentIndex-1) / 2;
}
array[childIndex] = temp;
}
/**
* 下沉调整
* @param array 待调整的堆
* @param parentIndex 要下沉的父节点
* @param length 堆的有效大小
*/
public static void downAdjust(int[] array, int parentIndex, int length) {
// temp保存父节点值,用于最后的赋值
int temp = array[parentIndex];
int childIndex = 2 * parentIndex + 1;
while (childIndex < length) {
// 如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子
if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
childIndex++;
}
// 如果父节点小于任何一个孩子的值,直接跳出
if (temp <= array[childIndex])
break;
//无需真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
array[parentIndex] = temp;
}
/**
* 构建堆
* @param array 待调整的堆
*/
public static void buildHeap(int[] array) {
// 从最后一个非叶子节点开始,依次下沉调整
for (int i = (array.length-2)/2; i >= 0; i--) {
downAdjust(array, i, array.length);
}
}
public static void main(String[] args) {
int[] array = new int[] {1,3,2,6,5,7,8,9,10,0};
upAdjust(array);
System.out.println(Arrays.toString(array));
array = new int[] {7,1,3,10,5,2,8,9,6};
buildHeap(array);
System.out.println(Arrays.toString(array));
}
}
代码中有一个优化的点,就是在父节点和孩子节点做连续交换时,并不一定要真的交 换,只需要先把交换一方的值存入temp变量,做单向覆盖,循环结束后,再把temp的值存入交换后的最终位置即可。
2.5 二叉堆的作用
二叉堆是实现堆排序及优先队列的基础。有一道很经典的算法题,在一个无序数组,要求找出数组中第k大的元素,这个就可以用二叉堆巧妙解决。下面,我们就来学习优先队列。
3、优先队列
既然优先队列中出现了“队列”两个字,那让我们先来回顾一下之前所介绍的队列的特性。
在之前的章节中已经讲过,队列的特点是先进先出(FIFO)。
入队列,将新元素置于队尾:
优先队列不再遵循先入先出的原则,而是分为两种情况。
- 最大优先队列,无论入队顺序如何,都是当前最大的元素优先出队
- 最小优先队列,无论入队顺序如何,都是当前最小的元素优先出队
例如有一个最大优先队列,其中的最大元素是8,那么虽然8并不是队头元素,但出队时仍然让元素8首先出队。

要实现以上需求,利用线性数据结构并非不能实现,但是时间复杂度较高。
3.1 优先队列的实现
先来回顾一下二叉堆的特性。
1. 最大堆的堆顶是整个堆中的最大元素。
2. 最小堆的堆顶是整个堆中的最小元素。
因此,可以用最大堆来实现最大优先队列,这样的话,每一次入队操作就是堆的插入操作,每一次出队操作就是删除堆顶节点。
入队操作具体步骤如下。
1、插入新节点5。
1. 让原堆顶节点10出队。
二叉堆节点“上浮”和“下沉”的时间复杂度都是O(logn),所以优先队列入队和出队的时间复杂度也是O(logn)!
3.2 优先队列的代码
public class PriorityQueue {
private int[] array;
private int size;
public PriorityQueue(){
//队列初始长度32
array = new int[32];
}
/**
* 入队
* @param key 入队元素
*/
public void enQueue(int key) {
//队列长度超出范围,扩容
if(size >= array.length){
resize();
}
array[size++] = key;
upAdjust();
}
/**
* 出队
*/
public int deQueue() throws Exception {
if(size <= 0){
throw new Exception("the queue is empty !");
}
//获取堆顶元素
int head = array[0];
//最后一个元素移动到堆顶
array[0] = array[--size];
downAdjust();
return head;
}
/**
* 上浮调整
*/
private void upAdjust() {
int childIndex = size-1;
int parentIndex = (childIndex-1)/2;
// temp保存插入的叶子节点值,用于最后的赋值
int temp = array[childIndex];
while (childIndex > 0 && temp > array[parentIndex])
{
//无需真正交换,单向赋值即可
array[childIndex] = array[parentIndex];
childIndex = parentIndex;
parentIndex = (parentIndex-1) / 2;
}
array[childIndex] = temp;
}
/**
* 下沉调整
*/
private void downAdjust() {
// temp保存父节点值,用于最后的赋值
int parentIndex = 0;
int temp = array[parentIndex];
int childIndex = 1;
while (childIndex < size) {
// 如果有右孩子,且右孩子大于左孩子的值,则定位到右孩子
if (childIndex + 1 < size && array[childIndex + 1] > array[childIndex]) {
childIndex++;
}
// 如果父节点大于任何一个孩子的值,直接跳出
if (temp >= array[childIndex])
break;
//无需真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
array[parentIndex] = temp;
}
/**
* 队列扩容
*/
private void resize() {
//队列容量翻倍
int newSize = this.size * 2;
this.array = Arrays.copyOf(this.array, newSize);
}
public static void main(String[] args) throws Exception {
PriorityQueue priorityQueue = new PriorityQueue();
priorityQueue.enQueue(3);
priorityQueue.enQueue(5);
priorityQueue.enQueue(10);
priorityQueue.enQueue(2);
priorityQueue.enQueue(7);
System.out.println("出队元素:" + priorityQueue.deQueue());
System.out.println("出队元素:" + priorityQueue.deQueue());
}
}
上述代码采用数组来存储二叉堆的元素,因此当元素数量超过数组长度时,需要进行扩容来扩大数组长度。
本篇博客中代码和彩图来源于《漫画算法》,应本书作者要求,加上本书公众号《程序员小灰》二维码。

感兴趣的朋友可以去购买正版实体书,确实不错,非常适合小白入门。

小结
- 什么是二叉堆?
二叉堆是一种特殊的完全二叉树,分为最大堆和最小堆。
在最大堆中,任何一个父节点的值,都大于或等于它左、右孩子节点的值。
在最小堆中,任何一个父节点的值,都小于或等于它左、右孩子节点的值。
- 什么是优先队列
优先队列分为最大优先队列和最小优先队列。
在最大优先队列中,无论入队顺序如何,当前最大的元素都会优先出队,这是基于最大堆实现的。
在最小优先队列中,无论入队顺序如何,当前最小的元素都会优先出队,这是基于最 小堆实现的。
如果本文对您有所帮助,不妨点个赞支持一下博主
希望我们都能在学习的道路上越走越远
![]()