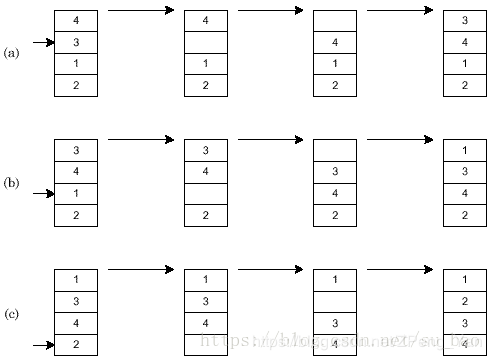
排序方法:冒泡,选择,快排,插入,并归,堆排
冒泡排序:相邻的元素进行比较(每一对),排序,(由小到大)
def bubble_sort(li):
for i in range(len(li)-1):
for j in range(len(li)-i-1):
if li[j] > li[j+1]:
li[j],li[j+1]=li[j+1],li[j]
li = [1,5,2,6,3,7,4,8,9,0]
bubble_sort(li)
print(li) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
选择排序:找到最小(大)值,放到起始位置(下标),继续寻找,完成后排序
def select_sort(list):
n=len(list)
for i in range(n-1): 循环 n-1 次
min_index=i
for j in range(i+1,n):
if list[ j ] < list[min_index]
min_index = j #重新赋值
if min_index != i : #判断是否和初始值一致 不一致代表找到真正的最小值,之后进行交换
list[ i ],list[min_index]=list[min_index],list[ i ]
if __name__="__main__"
a_list=[8,6,10,5]
select_sort(a_list)
print(a_list)
冒泡排序 的稳定性大于 选择性排序
快排
def quick(list):
if len(list) < 2:
return list
tmp = list[0] # 临时变量 可以取随机值
left = [x for x in list[1:] if x <= tmp] # 左列表
right = [x for x in list[1:] if x > tmp] # 右列表
return quick(left) + [tmp] + quick(right)
li = [4,3,7,5,8,2]
print quick(li) # [2, 3, 4, 5, 7, 8]
#### 对[4,3,7,5,8,2]排序
'''
[3, 2] + [4] + [7, 5, 8] # tmp = [4]
[2] + [3] + [4] + [7, 5, 8] # tmp = [3] 此时对[3, 2]这个列表进行排序
[2] + [3] + [4] + [5] + [7] + [8] # tmp = [7] 此时对[7, 5, 8]这个列表进行排序
'''
插入排序
插入排序原理
插入排序的核心在于,它把一个无序数列看成两个数列,假如第一个元素构成了第一个数列,那么余下的元素构成了第二个数列,很显然,第一个数列是有序的(因为只有一个元素嘛,肯定有序哦),那么我们把第二个数列的第一个元素拿出来插入到第一个数列,使它依然构成一个有序数列,直到第二个数列中的所有元素全部插入到第一个数列,这时候就排好序了。
def insert_sort(alist):
"""插入排序"""
n = len(alist)
for j in range(1, n):
# 控制将拿到的元素放到前面有序序列中正确位置的过程
for i in range(j, 0, -1):
# 如果比前面的元素小,则往前移动
if alist[i] < alist[i - 1]:
alist[i], alist[i - 1] = alist[i - 1], alist[i]
# 否则代表比前面的所有元素都小,不需要再移动
else:
break
if __name__ == '__main__':
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
print("原列表为:%s" % alist)
insert_sort(alist)
print("新列表为:%s" % alist)
# 结果如下:
# 原列表为:[54, 26, 93, 17, 77, 31, 44, 55, 20]
# 新列表为:[17, 20, 26, 31, 44, 54, 55, 77, 93]
归并算法
归并排序首先进行的是对序列拆分。
先把代码看成已经执行到最后一步,左部分和右部分都是排序好的,然后把他们的左部分和右部分再排序,剩下的几次排序可以采用嵌套递归来实现。
代码如下:
#归并排序
def merge_sort(alist):
n=len(alist)
if n<=1: #如果只有一个元素的话就不能再往下拆分了,直接返回
return alist #不断归并到最后一个列表只有一个元素,把自身返回即可。
mid=n//2 #中间位置下标
#left 采用归并排序后形成的新的有序的新的列表
left_li=merge_sort(alist[:mid]) #左部分列表,调用自身
#right 采用归并排序后形成的新的有序的新的列表
right_li=merge_sort(alist[mid:]) #右部分列表,调用自身
#这个时候返回的左部分是经过多次递归后形成的一个有序的左部分,右部分也是一样
#这个时候就要把左右两部分进行合并,将两个有序的子序列合并成一个新的整体。
#merge(left,right)
#接下来是合并
left_pointer,right_pointer=0,0 #left_pointer和right_pointer刚开始都应该指向第一个元素
result=[] #建立新的列表来存放合并的结果值
while left_pointer<len(left_li) and right_pointer<len(right_li): #当两个指针都没有走到头的时候执行判断大小,并选择小的加入result列表代码
if left_li[left_pointer] <=right_li[right_pointer]: #这里加等号是为了确保代码的稳定性
result.append(left_li[left_pointer])
left_pointer+=1
else:
result.append(right_li[right_pointer])
right_pointer+=1
#当一边游标到头另一边的游标还没有到头的时候,把剩下的追加上,到头的追加空列表,没到头的把剩下的全部追加上
result+=left_li[left_pointer:]
result+=right_li[right_pointer:]
#到这里排序的新列表制作完成
return result #把新生成的列表返回
if __name__ == '__main__':
alist = [54, 26, 93, 17, 77, 31, 44, 55,20]
print(alist)
sorted=merge_sort(alist)
print(sorted)
堆排
原理(用数组表示完全二叉树的层序,最小堆):
从最后一个叶子节点的父节点开始,比较该节点与子节点的大小;
如果父节点是最小值,继续比较前面的节点;如果父节点不是最小值,父节点与最小值节点交换位置,并且考虑该变换对最小值节点的子节点的影响;
直到比较到根节点
代码如下:
def HeapSort(input_list):
#调整parent结点为大根堆
def HeapAdjust(input_list,parent,length):
temp = input_list[parent]
child = 2*parent+1
while child < length:
if child+1 <length and input_list[child] < input_list[child+1]:
child +=1
if temp > input_list[child]:
break
input_list[parent] = input_list[child]
parent = child
child = 2*child+1
input_list[parent] = temp
if input_list == []:
return []
sorted_list = input_list
length = len(sorted_list)
#最后一个结点的下标为length//2-1
#建立初始大根堆
for i in range(0,length // 2 )[::-1]:
HeapAdjust(sorted_list,i,length)
for j in range(1,length)[::-1]:
#把堆顶元素即第一大的元素与最后一个元素互换位置
temp = sorted_list[j]
sorted_list[j] = sorted_list[0]
sorted_list[0] = temp
#换完位置之后将剩余的元素重新调整成大根堆
HeapAdjust(sorted_list,0,j)
print('%dth' % (length - j))
print(sorted_list)
return sorted_list
if __name__ == '__main__':
input_list = [50,123,543,187,49,30,0,2,11,100]
print("input_list:")
print(input_list)
sorted_list = HeapSort(input_list)
print("sorted_list:")
print(input_list)