数据结构与算法（十一）（常用的十大算法）

二分查找（非递归）

package binarysearchnorecursion;

public class BinarySearchNoRecur {
    public static void main(String[] args) {
        int[] arr = {1,3,8,10,11,67,100};
        System.out.println(binarySearch(arr,-8));
    }

    public static int binarySearch(int[] arr,int target){
        int left = 0;
        int right = arr.length-1;
        while(left <= right){
            int mid = (left + right)/2;
            if(arr[mid] == target){
                return  mid;
            }else if(arr[mid] > target){
                right = mid -1;
            }else{
                left = mid +1;
            }
        }
        return -1;
    }
}

分治算法

1.思想介绍：
a.分解，将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
b.解决，如果若干个小问题比较好解决，就直接解决，否则递归解决
c.合并，将若干个小问题的解合起来就是原问题的解
2.能解决的问题
二分搜索，归并排序，快速排序，汉诺塔
3.汉诺塔问题分析
a.如果只有一个盘，就直接将盘从A移动到C
b.如果盘数大于等于2，将所有盘分为两部分，最后一个盘自己一部分，剩下的盘一部分
c.先将剩下的盘移动到B，再将最后一个盘移动到C，最后将剩下的盘从B移动到C
4.代码实现

package dac;

public class Hanoitower {
    public static void main(String[] args) {
        hanoitower(3,'A','B','C');
    }

    public static void hanoitower(int num,char a,char b,char c){
        if(num == 1){
            System.out.println("将第1个盘从"+a+"移动到"+c);
        }else{
            hanoitower(num-1,a,c,b);
            System.out.println("将第"+num+"个盘从"+a+"移动到"+c);
            hanoitower(num-1,b,a,c);
        }
    }
}

动态规划算法

1.算法思想：与分治算法类似，也是将大问题转换成小问题，再解决小问题，区别在于动态规划算法，下一个子阶段的求解是建立在上一个子阶段的基础上，而分治算法，每个子阶段都是独立的
2.背包问题问题描述：

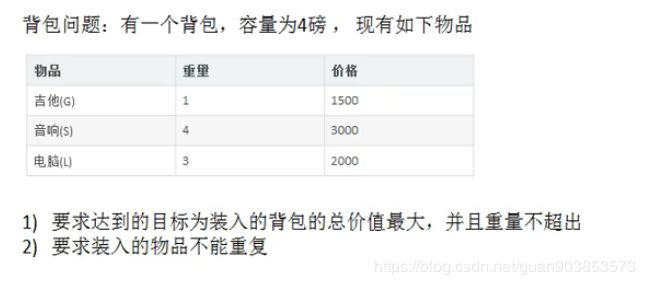
3.问题分析
a.分析动态规划算法可以使用画图的方式

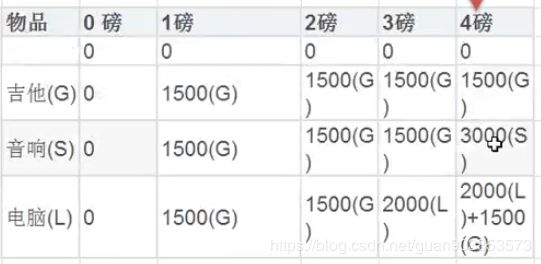
b.从上面的表格我们可以总结出规律：v[i][j]表示前i个物品能装入容量为j的容器的最大价值，val[i]表示第i个物品的价值，w[i]表示第i个物品的重量
v[i][0] = j[0][j] = 0表示第一行第一列全部为空
如果w[i]>j，代表当前物品的容量大于背包能承受的容量，所以直接延续上一个v[i][j] = v[i-1][j]
如果w[i]<=j,v[i][j] = max{v[i-1][j],val[i]+v[i-1][j-w[i]]},此时背包容量可以装下当前物品，所以就先装入当前物品，再去找剩下的容量可以装下的物品（最大价值）与上一个做对比，找到二者中最大的
4.代码实现

package dynamic;

public class KnapsackProblem {
    public static void main(String[] args) {
        int[] w = {1,4,3};//物品重量
        int[] vals = {1500,3000,2000};//物品价值
        int m = 4 ;//背包容量
        int n = w.length;//物品个数

        //表示前i个物品能装入容量为j的容器的最大价值
        int[][] v = new int[n+1][m+1];
        //标记可能出现的最大值
        int[][] path = new int[n+1][m+1];
        //将第一行第一列设置为空
        for(int i=0;i<v.length;i++){
            v[i][0] = 0;
        }
        for(int i=0;i<v[0].length;i++){
            v[0][i] = 0;
        }
        //比较w[i-1]与j的大小关系，分别填入数据
        for(int i=1;i<v.length;i++){
            for(int j=1;j<v[0].length;j++){
                if(w[i-1]>j){
                    v[i][j] = v[i-1][j];
                }else{
                    if(v[i-1][j]<vals[i-1]+v[i-1][j-w[i-1]]){
                        v[i][j] = vals[i-1]+v[i-1][j-w[i-1]];
                        path[i][j] = 1;
                    }else{
                        v[i][j] = v[i-1][j];
                    }
                }
            }
        }

        for(int i=0;i<v.length;i++){
            for(int j=0;j<v[i].length;j++){
                System.out.print(v[i][j]+" ");
            }
            System.out.println();
        }

        for(int i=0;i<v.length;i++){
            for(int j=0;j<v[i].length;j++){
                System.out.print(path[i][j]+" ");
            }
            System.out.println();
        }

        //找到最大匹配方式，从后向前找
        int i = path.length-1;
        int j = path[0].length-1;
        while (i>0 && j>0){
            if(path[i][j]==1){
                System.out.println(i);
                j -= w[i-1];
            }
            i--;
        }
    }
}

暴力匹配和KMP算法

1.暴力匹配（字符串）思路分析：
假设有字符串S1，S2，我们用S2（指针j）去S1（指针i）里面匹配，从0开始一个字符一个字符对比，如果相同就同时后移，如果发现不同S2指针直接移动到0，S1移动到i-j+1，再次匹配，此时效率很低
2.代码实现

package kmp;

public class ViolenceMatch {
    public static void main(String[] args) {
        String str1 = "AABCEDERQWWE";
        String str2 = "RQq";
        System.out.println(violenceMatch(str1,str2));
    }

    public static int violenceMatch(String str1,String str2){
        char[] chars1 = str1.toCharArray();
        char[] chars2 = str2.toCharArray();
        int length1 = str1.length();
        int length2 = str2.length();

        int i=0;
        int j=0;
        while(i<length1 && j<length2){
            if(chars1[i] == chars2[j]){
                i++;
                j++;
            }else{
            	i = i-j+1;
                j=0;
            }
        }
        if(j == length2){
            return i-j;
        }
        return -1;
    }
}

3.KMP算法思路分析
KMP和暴力匹配最大的不同在于，发现不同时，KMP并非是移动1位，而是通过算法移动n位，这样提高效率，在使用KMP时首先需要创造出部分匹配表，在使用部分匹配表完成移位，提高效率
4.代码实现

package kmp;

import java.util.Arrays;

public class KMPAlgorithm {
    public static void main(String[] args) {
        String str1 = "BBC ABCDAB ABCDABCDABDE";
        String str2 = "ABCDABD";
        int[] next = kmpNext(str2);
        System.out.println(Arrays.toString(kmpNext(str2)));
        System.out.println(kmp(str1,str2,next));
    }

    public static int kmp(String str1,String str2,int[] next){
        for(int i=0,j=0;i<str1.length();i++){
            while(j>0 && str1.charAt(i) != str2.charAt(j)){
                j = next[j-1];
            }
            if(str1.charAt(i) == str2.charAt(j)){
                j++;
            }
            if(j == str2.length()){
                return  i-j+1;
            }
        }
        return  -1;
    }

    //创建部分匹配表
    public static int[] kmpNext(String dest){
        int[] next = new int[dest.length()];
        next[0] = 0;
        for(int i=1,j=0;i<dest.length();i++){
            while(j>0 && dest.charAt(i) != dest.charAt(j)){
                j = next[j-1];
            }
            if(dest.charAt(i) == dest.charAt(j)){
                j++;
            }
            next[i] = j;
        }
        return next;
    }
}

贪心算法

1.算法简介：在问题进行求解时，在每一步选择中都采取最好或者最优的选择，但是得到的结果不一定是最优结果，但是会非常接近
2.问题描述

3.问题分析
遍历所有的广播电台，找到一个覆盖了最多的未覆盖地区的电台，将此电台存储起来，并在下次寻找时排除以前覆盖的地区，重复以上操作直到未覆盖地区为0
4.代码实现

package greedy;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;

public class GreedyAlgorithm {
    public static void main(String[] args) {
        HashMap<String, HashSet<String>>  hashMap = new HashMap<>();

        HashSet<String> hashSet1 = new HashSet<>();
        hashSet1.add("北京");
        hashSet1.add("上海");
        hashSet1.add("天津");

        HashSet<String> hashSet2 = new HashSet<>();
        hashSet2.add("广州");
        hashSet2.add("北京");
        hashSet2.add("深圳");

        HashSet<String> hashSet3 = new HashSet<>();
        hashSet3.add("成都");
        hashSet3.add("上海");
        hashSet3.add("杭州");

        HashSet<String> hashSet4 = new HashSet<>();
        hashSet4.add("上海");
        hashSet4.add("天津");

        HashSet<String> hashSet5 = new HashSet<>();
        hashSet5.add("杭州");
        hashSet5.add("大连");

        hashMap.put("K1",hashSet1);
        hashMap.put("K2",hashSet2);
        hashMap.put("K3",hashSet3);
        hashMap.put("K4",hashSet4);
        hashMap.put("K5",hashSet5);

        //表示全部城市
        HashSet<String>  allCitys = new HashSet<>();
        allCitys.add("北京");
        allCitys.add("上海");
        allCitys.add("天津");
        allCitys.add("成都");
        allCitys.add("大连");
        allCitys.add("杭州");
        allCitys.add("深圳");
        allCitys.add("广州");

        //表示最后要放入的频道
        ArrayList<String> list = new ArrayList<>();
        //本次循环中最优解
        String maxString = null;

        while(allCitys.size()>0){
            for(String key : hashMap.keySet()){
                HashSet s = hashMap.get(key);
                s.retainAll(allCitys);
                if(s.size()>0 && (maxString == null || s.size() > hashMap.get(maxString).size())){
                    maxString = key;
                }
                if(maxString != null){
                    list.add(maxString);
                    allCitys.removeAll(hashMap.get(maxString));
                }
                maxString = null;
            }
        }
        System.out.println(list);
    }
}

普利姆算法（Prim）

1.问题引出：

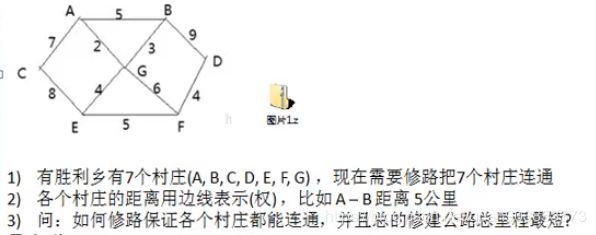
2.上述问题就是一个求最小生成树的问题

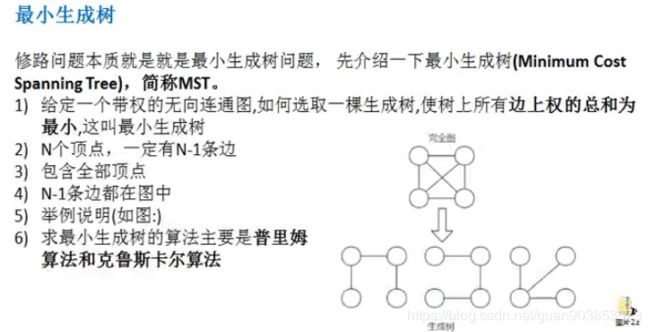
3.普利姆算法思路分析

4.代码实现

package prim;

import com.sun.org.apache.xml.internal.security.keys.content.MgmtData;

import java.util.Arrays;

public class PrimAlgorithm {
    public static void main(String[] args) {
        char[] verxArray = {'A','B','C','D','E','F','G'};
        int verxs = verxArray.length;
        int[][] weight = {
                {10000,5,7,10000,10000,10000,2},
                {5,10000,10000,9,10000,10000,3},
                {7,10000,10000,10000,8,10000,10000},
                {10000,9,10000,10000,10000,4,10000},
                {10000,10000,8,10000,10000,5,4},
                {10000,10000,10000,4,5,10000,6},
                {2,3,10000,10000,4,6,10000}
        };
        MGrap grap = new MGrap(verxs);
        minTree minTree = new minTree();
        minTree.createMGrap(grap,verxs,verxArray,weight);
        minTree.showMGrap(grap.weight);
        minTree.prim(grap,0);
    }
}

class minTree{
    //创建图
    public void createMGrap(MGrap grap,int verxs,char[] verxArray,int[][] weight){
        for(int i=0;i<verxArray.length;i++){
            grap.verxArray[i] = verxArray[i];
        }
        for(int i=0;i<weight.length;i++){
            for(int j=0;j<weight[0].length;j++){
                grap.weight[i][j] = weight[i][j];
            }
        }
    }
    //遍历图
    public void showMGrap(int[][] weight){
        for(int[] len : weight){
            System.out.println(Arrays.toString(len));
        }
    }
    //最小生成树
    public void prim(MGrap grap,int val){
        int[] visited = new int[grap.verxs];
        int h1 = -1;
        int h2 = -1;
        visited[val] = 1;
        for(int k=1;k<grap.verxs;k++){
            int maxLength = 10000;
            for(int i=0;i<grap.verxs;i++){
                for(int j=0;j<grap.verxs;j++){
                    if(visited[i] ==1 && visited[j] ==0 && grap.weight[i][j] < maxLength){
                        maxLength = grap.weight[i][j];
                        h1 = i;
                        h2 = j;
                    }
                }
            }
            System.out.println(grap.verxArray[h1]+","+grap.verxArray[h2]+","+maxLength);
            visited[h2] = 1;
        }
    }
}

//图
class MGrap{
    int verxs;//节点数量
    char[] verxArray;//存放节点的数组
    int[][] weight;//

    public MGrap(int verxs){
        this.verxs = verxs;
        verxArray = new char[verxs];
        weight = new int[verxs][verxs];
    }
}

Kruskal算法

1.问题引出

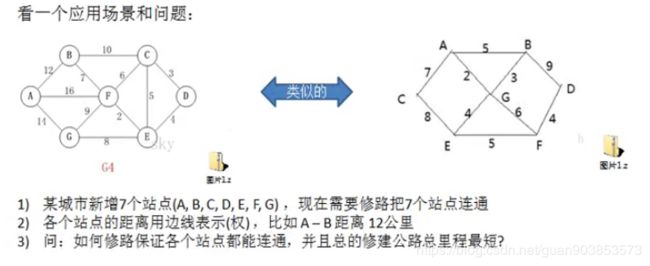
问题本质也是寻找最小生成树
2.Kruskal算法分析：
a.将所有边从小到大排序
b.按照从小到大的顺序加入到结果中，但是需要判断是否产生回路
c.回路的判断主要是看，边的两个节点是否指向同一终点
3.代码实现

package kruskal;


import java.util.ArrayList;
import java.util.Arrays;

public class KruskalCase {
    static final int max = -1;
    public static void main(String[] args) {
        char[] verxs = {'A','B','C','D','E','F','G'};
        int[][] weight = {
                {0,12,max,max,max,16,14},
                {12,0,10,max,max,7,max},
                {max,10,0,3,5,6,max},
                {max,max,3,0,4,max,max},
                {max,max,5,4,0,2,8},
                {16,7,6,max,2,0,9},
                {14,max,max,max,8,9,0}
        };
        MGrap grap = new MGrap(verxs.length,verxs,weight);
        grap.showGrap();
        Edge[] edges = getEdges(grap.weight,grap.verxs);
        System.out.println(Arrays.toString(edges));
        System.out.println("排序后:");
        Edge[] orderEdges = orderEdges(edges);
        System.out.println(Arrays.toString(orderEdges));
        kruskal(verxs.length,orderEdges.length,orderEdges,verxs);
    }

    //克鲁斯卡尔
    public static void kruskal(int verxLength,int edgesLength,Edge[] orderEdges,char[] verxs){
        int[] end = new int[verxLength];
        Edge[] lastEdge = new Edge[edgesLength];
        int index = 0;
        for(int i=0;i<edgesLength;i++){
            int c1 = orderEdges[i].start;
            int c2 = orderEdges[i].end;
            //此处需要寻找C1,C2在数组中的位置
            int c3 = findaddress(c1,verxs);
            int c4 = findaddress(c2,verxs);
            if(findEnd(end,c3) != findEnd(end,c4)){
                end[findEnd(end,c3)] = findEnd(end,c4);
                lastEdge[index++] = orderEdges[i];
            }
        }
        System.out.println(Arrays.toString(lastEdge));
    }

    //根据给定int数值去数组中寻找对应的位置
    public static int findaddress(int c,char[] verxs){
        for(int i=0;i<verxs.length;i++){
            if(verxs[i] == c){
                return i;
            }
        }
        return -1;
    }

    //找到当前节点的末位节点用来判断是否产生回路
    public static int findEnd(int[] end,int i){
        while(end[i] != 0){
            i = end[i];
        }
        return i;
    }
    //选择出当前图有效的边
    public static Edge[] getEdges(int[][] weight, char[] verxs){
        ArrayList<Edge> arrayList = new ArrayList<>();
        for(int i=0;i<weight.length;i++){
            for(int j=0;j<weight[i].length;j++){
                if(weight[i][j] != 0 && weight[i][j] != max){
                    arrayList.add(new Edge(verxs[i],verxs[j],weight[i][j]));
                }
            }
        }
        Edge[] edges = new Edge[arrayList.size()];
        for(int i=0;i<arrayList.size();i++){
            edges[i] = arrayList.get(i);
        }
        return edges;
    }

    //将选择出来的边进行排序
    public static Edge[] orderEdges(Edge[] edges){
        for(int i=0;i<edges.length-1;i++){
            for(int j=0;j<edges.length-1-i;j++){
                if(edges[j].length>edges[j+1].length){
                    Edge edge = edges[j];
                    edges[j] = edges[j+1];
                    edges[j+1] = edge;
                }
            }
        }
        return edges;
    }
}

//图
class MGrap{
    int verxNum;//节点数量
    char[] verxs;//节点数组
    int[][] weight;//存放边的信息

    public MGrap(int verxNum,char[] verxs,int[][] weight){
        this.verxNum = verxNum;
        this.verxs = new char[verxNum];
        this.weight = new int[verxNum][verxNum];

        for(int i=0;i<verxNum;i++){
            this.verxs[i] = verxs[i];
        }

        for(int i=0;i<verxNum;i++){
            for(int j=0;j<verxNum;j++){
                this.weight[i][j] = weight[i][j];
            }
        }
    }
    public void showGrap(){
        for(int[] len :weight){
            System.out.println(Arrays.toString(len));
        }
    }
}

//边
class Edge{
    char start;
    char end;
    int length;

    public Edge(char start, char end, int length) {
        this.start = start;
        this.end = end;
        this.length = length;
    }

    @Override
    public String toString() {
        return "Edge{" +
                "start=" + start +
                ", end=" + end +
                ", length=" + length +
                '}';
    }
}

Dijkstra（迪杰斯特拉）算法（最短路径）

1.问题引出：

2.Dijkstra（迪杰斯特拉）算法思路分析
需要创建3个数组，记录节点是否 被访问，记录节点到G的距离，记录节点的前置节点，之后遍历填充着3个数组，结束时记录节点到G的距离这个数组就是我们要的结果
3.代码实现

package dijkstra;

import java.util.Arrays;

public class DijkstraAlgorithm {
    public static void main(String[] args) {
        char[] vertxs = {'A','B','C','D','E','F','G'};
        int[][] weight = new int[vertxs.length][vertxs.length];
        final int N = 65535;
        weight[0] = new int[]{N,5,7,N,N,N,2};
        weight[1] = new int[]{5,N,N,9,N,N,3};
        weight[2] = new int[]{7,N,N,N,8,N,N};
        weight[3] = new int[]{N,9,N,N,N,4,N};
        weight[4] = new int[]{N,N,8,N,N,5,4};
        weight[5] = new int[]{N,N,N,4,5,N,6};
        weight[6] = new int[]{2,3,N,N,4,6,N};
        MGrap mg = new MGrap(vertxs,weight);
        mg.showGrap();
        mg.djs(6);
    }
}

//图
class MGrap{
    private char[] vertxs;//存放节点
    private int[][] weight;//邻接矩阵
    VisitedVertex vv ;

    public MGrap(char[] vertxs,int[][] weight){
        this.vertxs = vertxs;
        this.weight = weight;
    }

    //输出邻接矩阵
    public void showGrap(){
        for(int[] len : this.weight){
            System.out.println(Arrays.toString(len));
        }
    }

    //迪杰斯特拉
    public void djs(int index){
        vv = new VisitedVertex(vertxs.length,index);
        update(index);
        for(int j=1;j<vertxs.length;j++){
            index = vv.updateArr();
            update(index);
        }
        System.out.println("更新后");
        System.out.println(Arrays.toString(vv.already_arr));
        System.out.println(Arrays.toString(vv.dis));
        System.out.println(Arrays.toString(vv.pre_visited));
    }

    //更新index下标顶点到周围顶点的距离与前驱节点
    public void update(int index){
        int len = 0;
        for(int j=0;j<weight[index].length;j++){
            len = vv.getDis(index) + weight[index][j];
            if(!vv.in(j) && len < vv.getDis(j)){
                vv.updateDis(j,len);
                vv.updatePreVisited(j,index);
            }
        }
    }
}

//对已访问节点进行记录
class VisitedVertex{
    //对已访问节点进行记录
    public int[] already_arr;
    //记录节点的前驱节点
    public int[] pre_visited;
    //记录节点到初始节点的距离
    public int[] dis;

    public VisitedVertex(int length,int index){
        already_arr = new int[length];
        pre_visited = new int[length];
        dis = new int[length];

        already_arr[index] = 1;
        Arrays.fill(dis,65535);
        dis[index] = 0;
    }

    //判断index顶点是否被访问,true表示被访问过，false表示没有被访问过
    public boolean in(int index){
        return already_arr[index] == 1;
    }

    //更新出发节点到index节点的距离
    public void updateDis(int index,int len){
        dis[index] = len;
    }

    //更新前驱节点，将pre这个节点的前驱节点设置成index
    public void updatePreVisited(int pre,int index){
        pre_visited[pre] = index;
    }

    //返回出发顶点到index顶点的距离
    public int getDis(int index){
        return dis[index];
    }

    //继续选择并返回新的访问节点
    public int updateArr(){
        int min = 65535;
        int index = 0;
        for(int i=0;i<already_arr.length;i++){
            if(already_arr[i] ==0 && dis[i]<min){
                min = dis[i];
                index =i ;
            }
        }
        already_arr[index] = 1;
        return index;
    }
}

弗洛伊德算法（最短路径）

1.弗洛伊德算法与迪杰斯特拉算法的区别，弗洛伊德算法能求出每个节点到每个节点的最小路径，而迪杰斯特拉只能求出当前节点到所有节点最小路径
2.问题

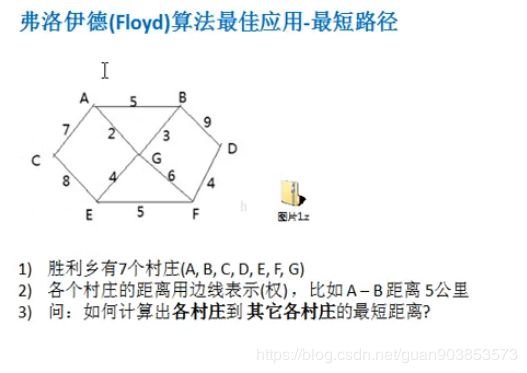
3.代码实现

package floyd;

import java.util.Arrays;

public class Floyd {
    public static void main(String[] args) {
        char[] verts = {'A','B','C','D','E','F','G'};
        int[][] weight = new int[verts.length][verts.length];
        final int N = 65535;
        weight[0] = new int[]{0,5,7,N,N,N,2};
        weight[1] = new int[]{5,0,N,9,N,N,3};
        weight[2] = new int[]{7,N,0,N,8,N,N};
        weight[3] = new int[]{N,9,N,0,N,4,N};
        weight[4] = new int[]{N,N,8,N,0,5,4};
        weight[5] = new int[]{N,N,N,4,5,0,6};
        weight[6] = new int[]{2,3,N,N,4,6,0};
        Gray gray = new Gray(verts,weight);
        gray.floyd();
        gray.show();
    }
}

class Gray{
    private char[] vertx;//节点数字
    private int[][] weight;//邻接矩阵
    private int[][] pre;//前驱节点

    public Gray(char[] vertx,int[][] weight){
        this.vertx = vertx;
        this.weight = weight;
        pre = new int[vertx.length][vertx.length];

        for(int i=0;i<vertx.length;i++){
            Arrays.fill(pre[i],i);
        }
    }

    public void show(){
        for(int[] len : weight){
            System.out.println(Arrays.toString(len));
        }
        for(int[] len : pre){
            System.out.println(Arrays.toString(len));
        }
    }

    public void floyd(){
        int len = 0;
        //k表示中间节点
        for(int k=0;k<vertx.length;k++){
            //i表示出发节点
            for(int i =0;i<vertx.length;i++){
                //j表示终点
                for(int j=0;j<vertx.length;j++){
                    len = weight[i][k]+weight[k][j];
                    if(len<weight[i][j]){
                        weight[i][j] = len;
                        pre[i][j] = pre[k][j];
                    }
                }
            }
        }
    }
}

骑士周游问题

1.问题描述：

2.思路分析：
首先需要准备一个二维数组表示棋盘，准备一个一维数组表示是否访问过，将当前节点设置为已访问，并寻找当前节点下一步可以走的节点，放入集合中，遍历集合，如果下一个节点没有被访问过，就递归处理，退出递归有两种情况，①走不下去啦，将当前节点设置为未访问状态②走完啦，退出方法
3.代码实现

package horse;

import java.awt.*;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;

public class HorseChessboard {
    static final int X = 6;
    static final int Y = 6;
    static int[][] chess = new int[X][Y];
    static int[] record = new int[X*Y];
    static boolean finished;
    public static void main(String[] args) {
        traversal(chess,3,1,1);
        for(int[] len :chess){
            System.out.println(Arrays.toString(len));
        }
    }

    public static void traversal(int[][] chess,int x,int y,int step){
        chess[y][x] = step;
        record[y*X+x] = 1;
        ArrayList<Point> arrayList = findPoints(new Point(x,y));
        sort(arrayList);
        while(!arrayList.isEmpty()){
            Point point = arrayList.remove(0);
            if(record[point.y*X+point.x] == 0){
                traversal(chess, point.x, point.y, step+1);
            }
        }
        if(step<X*Y && !finished){
            chess[y][x] = 0;
            record[y*X+x] = 0;
        }else{
            finished = true;
        }
    }

    //获取当前节点可以走的路
    public static ArrayList<Point> findPoints(Point point){
        ArrayList<Point> arrayList = new ArrayList<>();
        Point p = new Point();
        if((p.x = point.x-2) >=0 && (p.y = point.y-1) >= 0){
            arrayList.add(new Point(p));
        }
        if((p.x = point.x-1) >=0 && (p.y = point.y-2) >= 0){
            arrayList.add(new Point(p));
        }
        if((p.x = point.x+1) < X && (p.y = point.y-2) >= 0){
            arrayList.add(new Point(p));
        }
        if((p.x = point.x+2) < X && (p.y = point.y-1) >= 0){
            arrayList.add(new Point(p));
        }
        if((p.x = point.x+2) <X && (p.y = point.y+1) <Y){
            arrayList.add(new Point(p));
        }
        if((p.x = point.x+1) <X && (p.y = point.y+2) <Y){
            arrayList.add(new Point(p));
        }
        if((p.x = point.x-1) >=0 && (p.y = point.y+2) <Y){
            arrayList.add(new Point(p));
        }
        if((p.x = point.x-2) >=0 && (p.y = point.y+1)<Y){
            arrayList.add(new Point(p));
        }
        return arrayList;
    }

    //使用贪心算法优化，每次先选择ps中下一个节点对应下一个节点数少的优先递归，提高效率
    public static void sort(ArrayList<Point> ps){
        ps.sort(new Comparator<Point>() {
            @Override
            public int compare(Point o1, Point o2) {
                int count1 = findPoints(o1).size();
                int count2 = findPoints(o2).size();
                if(count1 > count2){
                    return 1;
                }else if(count1 == count2){
                    return 0;
                }else {
                    return -1;
                }
            }
        });
    }
}