python numpy的常用aip方法及操作!免费开源!!!!
一些简单的用法列出来,稍稍绕的给大家上图!
(1)基础代码
num=[1,2,3]
print(num)
(2)生成矩阵 (array arange floor random linspace zeros ones eye empty)
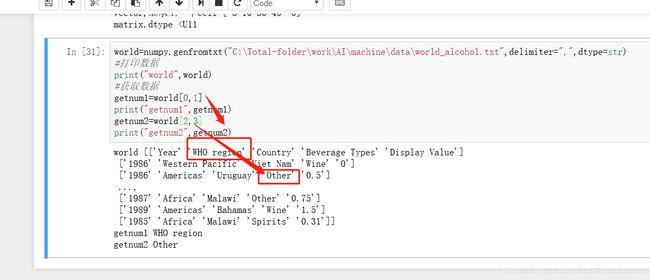
world=numpy.array([1,2,3])
print("world",world)
matrix=numpy.array([[1,2,3],[4,5,6]])
print("matrix",matrix)
print("numpy.arange(15)",numpy.arange(15))
# 随机构造一个0-1区间的值 random((2,3))2行3列
print("numpy.random.random((2,3))",numpy.random.random((3,5)))
print(numpy.linspace(0,30,100))
# 求正弦 余弦一类的方法
# print(numpy.sin(numpy.linspace(0,30,50)))#正弦 0到-1
print(numpy.cos(numpy.linspace(0,30,50))) #余弦1到1
# 初始化一个矩阵 值为0
matrix=numpy.zeros((3,4),dtype=numpy.int32)
print("matrix值为0的数字类型矩阵",matrix)
# 初始化一个矩阵 值为1
matrix=numpy.ones((3,4),dtype=numpy.str)
print("matrix值为1的字符串矩阵",matrix)
a_eye = numpy.eye(3) # 创建3阶单位矩阵
print("a_eye",a_eye)
a_empty = numpy.empty((3,4)) # 创建3*4的空矩阵
print("a_empty",a_empty)
# 把数据进行拆分--横向切割
a=numpy.floor(10*numpy.random.random((12,2)))#0-9 分成12行2列
print("a",a)
b=numpy.vsplit(a,3)#按列拆分3份 列自动生成
# print("b按列拆分3份",b)
print("竖着3 5的位置切割",numpy.vsplit(a,(3,5)))
(3)获取矩阵中的部分数据,生成一个新的矩阵
(4)矩阵的操作 shape ndim size
shape
### 通过切片读取数据
matrix=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
# print("matrix.shape",matrix.shape)#矩阵结构(3, 3)
# getnum3=matrix[:,1]#读取每一行第二条数据(索引值为1)
# print("getnum3",getnum3)
# getnum3=matrix[1,:]#读取第二行每条数据(索引值为1)
# print("getnum3",getnum3)#[4 5 6]
# getnum3=matrix[1,1:3]#读取第二行每条数据(索引值为1)
# print("getnum3",getnum3)#读取第列的 2 3条数据 [5 6]
# getnum3=matrix[0:2,1:3]#读取第1,2行 的 2,3每条数据
# print("getnum3",getnum3)#2 3条数据 [[2 3],[5 6]]
getnum3=matrix[1,0]#读取第2行 的 第一每条数据
print("getnum3",getnum3)#4
方法 :
(最大值,最小值)min max
# array自带的api方法 最大 最小值
matrix=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
# print(",第一行的每一列,matrix最小",matrix[0,:].min())#1
# print("第一行的每一列,matrix最大值",matrix[0,:].max())#3
# print("help(numpy.array)",help(numpy.array))
(查看维度) ndim
# 常见的api方法
# 生成一个范围的以为数组
# print("numpy.arange(15)",numpy.arange(15))#[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
# 通过reshape生成多维的矩阵 3行3列
matrix=numpy.arange(64).reshape(4,4,4)
# print("matrix",matrix)
# print("matrix.shape查看结构",matrix.shape)
# print("matrix.ndim查看维度",matrix.ndim)#3
print("matrix.size值的数量",matrix.size)#64
(排序)sort (合并,拆分)hstack vstack hsplit vspit
sort
# 数据排序
a=numpy.array([[10,11,4,5,6,7],[8,9,1,2,3,12]])
b=numpy.sort(a,axis=1)#按列排序 y轴
print("b",b)#[[ 4 5 6 7 10 11][ 1 2 3 8 9 12]]
# print("numpy.flip(b,axis=0)",numpy.flip(b,axis=0))
#[[ 1 2 3 8 9 12][ 4 5 6 7 10 11]]从小到大
print("numpy.flip(b,axis=1)",numpy.flip(b,axis=1))
#[[11 10 7 6 5 4][12 9 8 3 2 1]] 从大到小
# b=numpy.sort(a,axis=0)#按行排序 (8<10,9<11,1<4,2<5,3<6,12>7 所以7排第一行)
# print("b",b)#[[ 8 9 1 2 3 7][10 11 4 5 6 12]]
hstack vstack
# 两个数据拼接
a=numpy.array([[1,2],[3,4]])
b=numpy.array([[5,6],[7,8]])
c=numpy.hstack((a,b))
print("横向拼接",c)#[[1 2 5 6][3 4 7 8]] [a1+b1][a2+b2]
c=numpy.vstack((a,b))
print("纵向拼接",c)#[[1 2][3 4][5 6][7 8]]
hsplit
# 把数据进行拆分--横向切割
a=numpy.array([1,2,3,4,5,6,7,8,9,10,11,12])
# b=numpy.hsplit(a,3)#按行拆分3份 列自动生成
# print("b按行拆分3份",b)
print("按照指定位置切割3,5,8",numpy.hsplit(a,(3,5,8)))
vspit
# 把数据进行拆分--横向切割
a=numpy.floor(10*numpy.random.random((12,2)))#0-9 分成12行2列
print("a",a)
b=numpy.vsplit(a,3)#按列拆分3份 列自动生成
# print("b按列拆分3份",b)
print("竖着3 5的位置切割",numpy.vsplit(a,(3,5)))
(结构的变化)shape(3,4) reshape() ravel()多维变 一维
# 随机取整矩阵 1-10 3行4列
a=numpy.floor(10*numpy.random.random((3,4)))
# print("a",a)
# 从多维矩阵变为一维向量
b=a.ravel()#把3行4列 12个数据整合成一个列表
# print("b",b)#[ 9. 0. 9. 9. 3. 0. 4. 5. 7. 3. 0. 8.]
# 对新得到的向量重新组合
b.shape=(6,2)
# print("b",b)#[[ 1. 5.][ 8. 9. ][ 7. 6.] [ 8. 6.][ 9. 3.][ 1. 3.]]
# 可以把行和列转换
# print("b.T",b.T)#把6行2列 转变成2行6列 [[ 0. 0. 4. 4. 7. 0.][ 3. 0. 5. 3. 7. 2.]]
# reshape是重新排序,按照不同行、列 有时候行确定了,列也就自然确定了 -1自动算列数
print("b.reshape(3,-1)",b.reshape(3,-1))#固定3行 -1自动算列
复制:
深度复制: 浅度复制: copy
# 复制:深度复制,公司同用一个内存空间
# a=numpy.arange(12)
# b=a
# print("a",a)#[ 0 1 2 3 4 5 6 7 8 9 10 11]
# print("b is a",b is a)#True
# print("id(a)",id(a),"id(b)",id(b))#id(a) 1476229887760 id(b) 1476229887760
# b.shape=(3,4)
# b改变,a也随之改变
# print("b",b)#[[ 0 1 2 3][ 4 5 6 7][ 8 9 10 11]]
# print("a",a)#[[ 0 1 2 3][ 4 5 6 7][ 8 9 10 11]]
# 复制:浅度复制,内存空间不同 但是公用的是一套值
a=numpy.arange(12)
b=a.view()
print("a",a)#[ 0 1 2 3 4 5 6 7 8 9 10 11]
print("b is a",b is a)#False
print("id(a)",id(a),"id(b)",id(b))#id(a) 1476229209104 id(b) 1476229207424不一样了
b[1]=123
# b改变,a也随之改变
print("b",b)#[ 0 123 2 3 4 5 6 7 8 9 10 11]
print("a",a)#[ 0 123 2 3 4 5 6 7 8 9 10 11]
#copy的复制方法 空间不共享 数据也不共享
a=numpy.arange(12)
b=a.copy()
print("a",a)#[ 0 1 2 3 4 5 6 7 8 9 10 11]
print("b is a",b is a)#False
print("id(a)",id(a),"id(b)",id(b))#id(a) 1476221519392 id(b) 1476229195456不一样了
b[1]=123
#a不随着b改变而改变
print("b",b)#[ 0 123 2 3 4 5 6 7 8 9 10 11]
print("a",a)#[ 0 1 2 3 4 5 6 7 8 9 10 11]
总结来说:深度复制是值一样 id值也一样 浅度复制虽然id值不一样 两者不相等但是值相等
矩阵中按照行、列来获取最大值所在的索引 argmax
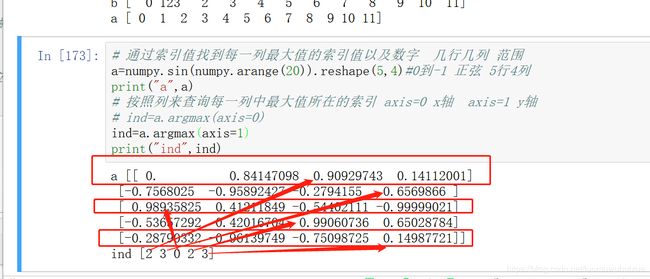
# 通过索引值找到每一列最大值的索引值以及数字 几行几列 范围
a=numpy.sin(numpy.arange(20)).reshape(5,4)#0到-1 正弦 5行4列
print("a",a)
# 按照列来查询每一列中最大值所在的索引 axis=0 x轴 axis=1 y轴
ind=a.argmax(axis=0)
# ind=a.argmax(axis=1)
print("ind",ind)
# a.shape5行 4 [0]代表行5 [1]代表列4
# print("a.shape[1]",a.shape[1])#读取矩阵的(行,列)长度
# 对应索引处的值取出来,
# 列确定了,需要查看每一行对应这一列的索引处的数据
print("range(a.shape[1]",range(a.shape[1]))#range(0, 4)
数学计算 + - * (**)
# 矩阵的数学计算
a=numpy.array([20,30,40,50])
b=numpy.arange(4)
# print("a",a)#[ 20. 30. 40. 50.]
# print("b",b)#[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39]
print("a*b",a*b)#0*20 1*30 2*40 3*50 [ 0. 30. 80. 150.]
print("b**2",b**2)# 0*0 1*1 2*2 3*3 2次幂来计算[0 1 4 9]
print("a<35",a<35)#[ True True False False]
矩阵积:一个矩阵的行*另外一个矩阵的列 相加**
# 乘法的计算,矩阵积
a=numpy.array([[1,3],
[0,1]])
# print("a",a)
b=numpy.array([[2,0],
[3,4]])
# print("b",b)
# print("a*b",a*b)#1*2 1*0 0*3 1*4 [[2 0] [0 4]]
# dot如果是二维 就是计算矩阵积 第一个矩阵的行*第二个矩阵的列表
print("a.dot(b)",a.dot(b))#第一行*第一列1*2+3*3=11 第1行*第2列 1*0+3*4=12
# [[11 12] [ 3 4]] #第二行*第一列0*2+1*3=3 第2行*第2列 0*0+1*4=4
# 对现有的ndarry类型数据扩展操作
a=numpy.arange(0,40,10)#0-40步长为10
print("a",a)#[ 0 10 20 30]
b=numpy.tile(a,(3,2))#同样的数据 3行2列
print("b",b)
整体截图:
如果对您有帮助,请点赞支持,有问题请留言或私信,谢谢!
不足之处请指出,互相学习!