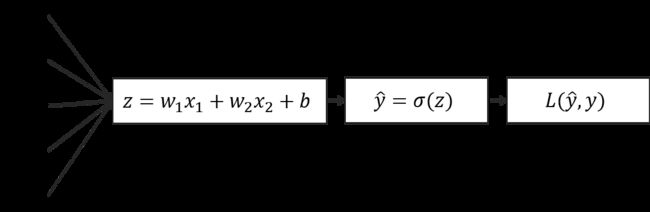深度学习知识点盘点(一)
最近博主在学习深度学习,选择的是看吴恩达的DeepLearning课程,因为Coursera上完成课程要申请助学金不然要钱(白嫖警告),并且要完成作业。博主没那么多时间也没那么多钱,所以选择了b站上刷视频。刷视频的时候就边看边作总结,本来找了一些比较著名的笔记,一看发现还是字幕比较多,不利于复习,所以对部分常用的深度学习概念做了一些知识点盘点,然后又决定发到博客上,所以我尽量以看得懂的形式记录,希望在大家某天想找某个知识点的时候可以通过这篇博客得到帮助。
为什么深度学习会兴起
原因1. 在大规模的数据集上深度学习的性能比传统机器学习的更好
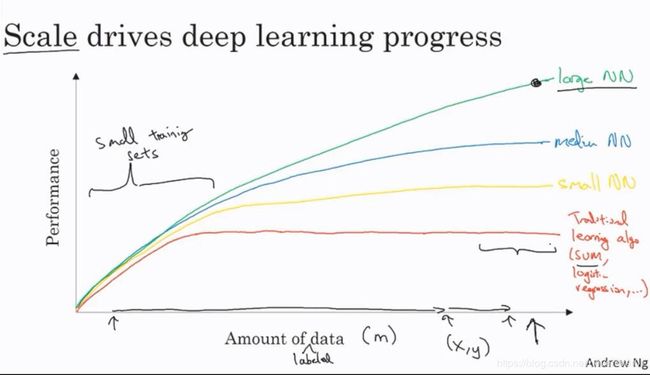
这张图是吴恩达在解释的时候画的,意思是在数据集规模比较小的时候,传统机器学习的表现非常好,但是在数据集规模变得非常巨大之后,深度学习相对传统机器学习的优势就变得非常明显了。它的表现可以大幅度超越传统机器学习。
在数据集比较小的时候,机器学习算法之间的优劣并不明显,通常差别都是发生在对数据集的处理以及手工实现机器学习算法时候的细节处理。
原因2. 在深度学习领域的算法创新,如ReLU
之前一直使用的激活函数都是sigmoid函数,但是它有一些固有缺点,在ReLu函数被设计出来之后,深度学习的性能和训练时间得到了大幅提升,使他变得更加popular了。
逻辑回归
逻辑回归是神经网络最基本的组成部分,一个完整的神经网络可以拆分成许多个逻辑回归单元
1. 用途:
二分类问题,也就是在机器学习中的逻辑回归
作为神经网络的单元
2. 公式:
y ^ = σ ( w T x + b ) \hat{y}=σ(w^Tx+b) y^=σ(wTx+b)
3. sigmoid函数:
σ ( z ) = 1 1 + e − z \sigma(z)=\frac{1}{1+e^{-z}} σ(z)=1+e−z1
通常逻辑回归都是使用sigmoid函数作为激活函数的。
4. 损失函数:
L ( y ^ , y ) = − y l o g ( y ^ ) − ( 1 − y ) l o g ( 1 − y ^ ) L(\hat{y},y)=-ylog(\hat{y})-(1-y)log(1-\hat{y}) L(y^,y)=−ylog(y^)−(1−y)log(1−y^)
这是二分类问题最常用的损失函数,称为交叉熵损失函数,上面式子是单个样本的交叉熵损失函数,完整的交叉熵损失函数需要将所有样本的损失累加起来,这里就不写了。
它的简单推导过程如图:

5. 逻辑回归的计算图模型
激活函数
为什么激活函数需要是非线性的
因为如果激活函数是线性的话,无论神经网络有多少层,它都是在计算线性函数,最终结果都是线性的,100层和10层没有任何区别。纯线性的神经网络只能划分出一条线性决策平面,然而大多数情况下决策平面都不是线性的,其拟合复杂函数的能力就不存在了。
下面是几种常用的激活函数形式
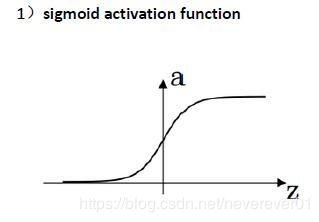
1. sigmoid函数
公式:
σ ( z ) = 1 1 + e − z \sigma(z)=\frac{1}{1+e^{-z}} σ(z)=1+e−z1
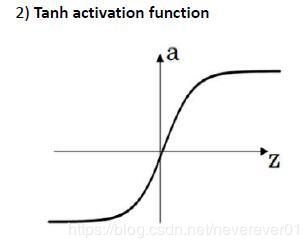
2. tanh函数
公式:
t a n h ( z ) = e z − e − z e z + e − z tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} tanh(z)=ez+e−zez−e−z

tanh激活函数的优点:可以使得数据的平均值更接近0而不是0.5,让下一层学习更简单一点(可以理解为做了类似归一化的操作)
tanh函数在几乎所有场合都优于sigmoid函数,除了在二分类的输出层,因为需要输出为(0,1)而可以sigmoid函数,其余情况下基本不会使用sigmoid而使用tanh。
3. ReLu函数 修正线性单元函数
公式:
R e L u ( z ) = m a x ( 0 , z ) ReLu(z)=max(0,z) ReLu(z)=max(0,z)

只要z值为正,ReLu的导数恒为1,当z为复数的时候,ReLu的导数恒为0,当z刚好等于0的时候,可以对其导数单独赋值,一般赋值为0.
4. Leaky ReLu函数
公式:
L e a k y R e L u ( z ) = { 0.01 z , z < 0 z , z > 0 0 , z = 0 LeakyReLu(z)=\begin{cases} 0.01z, \quad &z<0 \\ z, \quad &z>0 \\ 0, \quad &z=0 \end{cases} LeakyReLu(z)=⎩⎪⎨⎪⎧0.01z,z,0,z<0z>0z=0
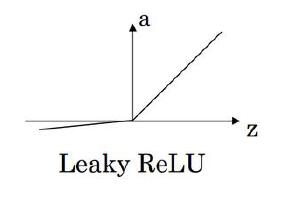
这个函数通常要比ReLu效果要好,尽管在实际中使用leaky的不多
ReLu和leaky ReLu的优点
- 在z的值变动很大的时候(横轴很广)激活函数的导数都很容易计算,而sigmoid函数的导数则需要很复杂的运算才能得到,因此实际中使用ReLu激活函数的神经网络学习的要比sigmoid的要快
- sigmoid和tanh函数的导数在z很大或者很小的时候都会出现梯度消失的情况(导数接近0)使得学习变得非常慢,而ReLu就不会有这个问题,它的导数值是恒定的。
神经网络的初始化和调参
对于神经网络,把权重全部初始化为0是不行的
如果将所有的权重都初始化为0,你会发现每一层的a值都是0(都是相等的),梯度下降就不会进行任何更新。
但是在逻辑回归的时候(只有一层的神经网络)就可以初始化为0,或者将偏置项初始化为0。
神经网络权重初始化的策略
将权重随机初始化。比如生成一个随机数,然后乘以0.001。
要保证每层的权重都是不一样的
为什么还要乘以0.001
假设激活函数使用tanh,它的计算步骤是这样的:
z = W x + b a = t a n h ( z ) z=Wx+b \\ a=tanh(z) z=Wx+ba=tanh(z)
当初始权重W很大的时候,z就会很大,在这种情况下可能会停在tanh函数比较平坦的地方,导致梯度下降变得很慢。如果W十分接近0,z就会很小,会在tanh函数斜率比较大的地方开始,梯度下降就会比较快。
神经网络中的超参数
什么是超参数
两个条件:(1)需要使用者手动设置的参数,(2)这些参数实际上控制了最后的权重值。
比如学习率 η \eta η,迭代次数,隐藏层的数量,隐藏层每一层的节点数量等等,这些都是超参数。
一般超参数是怎么设置的
想法->编码->实验->想法
这是一个很经验性的过程,必须通过一定的尝试和实践才能找到最合适的超参数,当然需要在一定理论的指引下进行尝试,不能盲目尝试。
深层神经网络的优化
训练集,验证集和测试集的划分
为什么要特地分出验证集
先看下各个数据集的作用是什么
- 训练集:训练模型,这个不用说了
- 测试集:评估训练好的模型的性能
那么在训练模型之后是不是可以直接放到测试集里面呢?一般是可以的,但是别忘了还有超参数,包括隐藏层数量,隐藏单元的数量,等等。每次确定一个超参数,就相当于一个新模型,就要重新评估一次(有可能需要重新训练),而这些超参数并不是一开始就能完全确定的,需要逐个比较哪个超参数下的模型比较好,那怎么比较呢?千万不能把多个模型放到测试集里面看看哪个好,测试集仅仅是用来作为最终评估的,在那之前,绝对不能使用测试集,因为这样会造成数据泄露,使得模型提前适应测试集,并且这样最后挑选出来的模型也仅仅是在测试集上表现良好罢了,这样训练出来的模型是毫无意义的。可以把测试集看成一个只能用一次的资源,所有准备就绪了才能用。这时候验证集的作用就体现出来了,它就是用来挑选超参数的。所以
3. 验证集:用来选择模型(包括选择超参数等等)
每个数据集怎么划分大小
在数据集比较小的时候(几万的级别),通常的做法是:60%训练,20%验证,20%测试
但是数据集比较庞大的时候(几百万的级别),验证集和测试集在总数据中的占比就会变得更小,一般是:98%训练,1%验证,1%测试。或者99.5%训练,0.25%验证,0.25%测试。
神经网络的训练
偏差和方差问题
偏差和方差的解决方案分类常见的就几种,列成表格就像下面这样:
| 问题 | 偏差高(high bias) | 方差高(high variance) |
|---|---|---|
| 换一个更大的网络 | 使用正则化 | |
| 迭代更多次 | 使用更多数据训练 | |
| 使用其他优化方法 | ----- |