LeetCode Week2: Maximum Subarray、Merge k Sorted Lists

　　这周主要实现了LeetCode Algorithms中的Divide-And-Conquer的题目，这里选择二道题来分析，分别是Maximum Subarray(easy)、Merge k Sorted Lists(Hard)。

一、Maximum Subarray

题目描述：Find the contiguous subarray within an array (containing at least one number) which has the largest sum.

For example, given the array [-2,1,-3,4,-1,2,1,-5,4],
the contiguous subarray [4,-1,2,1] has the largest sum = 6.

分析：这个题最开始的做法是采用了分治法，参考《算法分析》4.1的最大子数组问题。考虑最大值会出现的三种情况，即将数组分为三个部分，最大子序列可能会是前半部分或后半部分或者是跨越了中点的序列中，比如 S1max 、 S2max 、 S3max 。

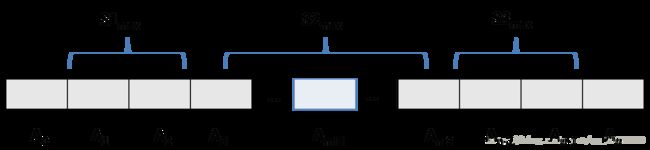
• 对于 S2max 对应的序列，从中间点开始，往左部分的序列和是左边序列的最大序列和，往右部分的序列亦然。这样的话可以直接从中点分别往左和右开始计算，得出两边的最大序列和，那么跨越中点可以得到的最大序列和就是两边序列和的累加；

• 对于 S1max 、 S3max 对应的序列，可以直接递归调用上述分割过程，对左数组（ A0 …… Amid ）和右数组（ Amid …… An ）和跨越中点的序列分别求其最大子序列的和；

---

　　最终返回三种计算中的最大的序列和即可。这样的做法的时间复杂度是 T(n)=2T(n2)+O(n) ，套用大师定理即可得到 T(n)=O(nlogn) 。

　　分治法的结果如下：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
       return findMaxArray(nums,0,nums.size()-1);
    }
    int findMaxArray(vector<int>& nums,int low, int high){
        if(high == low){
            return nums[low];           
        }
        else{
            int mid = (high+low)/2;
            return max(findMaxArray(nums,low,mid),findMaxArray(nums,mid+1,high),findMaxCrossArray(nums,low,mid,high));  
        }
    }

    int findMaxCrossArray(vector<int>& nums, int low, int mid, int high){
        int leftsum = -100, rightsum = -100;
        int sum = 0;
        for(int i = mid; i >= low;i--)
        {   
            sum += nums[i];
            if(sum>leftsum)
                leftsum = sum;
        }
        sum = 0;
        for(int i = mid+1; i <=high ;i++)
        {
            sum += nums[i];
            if(sum>rightsum)
                rightsum = sum;
        }
        return leftsum+rightsum;
    }    

    int max(int m1,int m2,int m3){
        if(m1>=m2 && m1>=m3)
            return m1;
        else if(m2>=m1 && m2>=m3)
            return m2;
        else 
            return m3;  
    }
};

　　但是，这样的分治法，其实是很麻烦的，RunTime为13ms。可以直接通过优化把算法的复杂度降到 O(n) 。

　　对于数组，我们可以这样考虑：

　　我们定义 SUMnow 为当前的序列的和， SUMmax 是已经读取到的序列中可以计算出的最大序列和。现在考虑加上下一个元素之后的新的 SUMnow :

• 下一个元素本身就比 SUMnow 大的话，那么就从这个元素开始，重新计算 SUMnow ；
• 如果 SUMnow > SUMmax ， SUMmax = SUMnow 。

---

　　代码的过程可以写作下面的形式：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum_now = 0;
        int sum_max = nums[0];
        for(int i = 0;i < nums.size();i++){
            sum_now += nums[i];
            if(nums[i]>= sum_now)
                sum_now = nums[i];
            if(sum_now >= sum_max)
                sum_max = sum_now;
        }
        return sum_max;
    }
};

　　可以看出此时的算法的复杂度只有 O(n) 了，通过提交发现RunTime也变为了9ms，得到了很大的提升。
　　

二、Merge k Sorted Lists

题目描述： Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity. Subscribe to see which companies asked this question.

分析：其实这个题的难度并不大，可以直接通过归并排序完成。最主要的就是了解归并排序的流程。
　　
　　归并排序是典型的分治模式的算法，它主要是通过把 n 个元素分成各有 n2 个元素的两个子序列，排序两个子序列，最后合并两个子序列。而 n2 个元素还可以分为两个元素数为 n4 的子序列，重复进行排序和合并，即为归并排序。归并排序的关键是“合并”。
　　
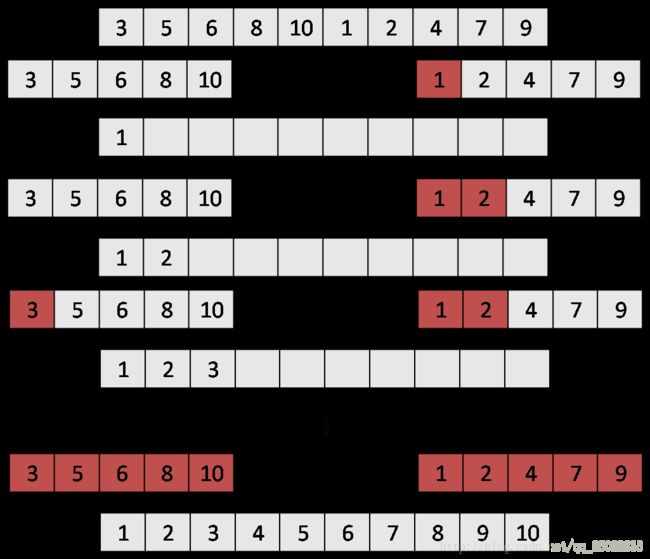
　　如下图所示，这里我们假设某一段序列长度为10，我们将其对半分成两个子序列后对其分别排序，之后将两个序列合并。每次都取出两个序列较小的一个元素，被选择的序列下一次被用来对比的就是下一位元素。这样子不断的对比选择，就能把两个子序列合并了。

　　

　　题目要求的是对多条链表的合并，需要注意的是链表的长度都是不一致，所以需要在合并过程时判断是否应该继续用某一序列的下一位来判断取值。

　　代码如下所示：

class Solution {
public:
    ListNode* mergeKLists(vector& lists) {
        if(lists.empty())
            return nullptr;
        return mergesort(lists,0,lists.size()-1);
    }
    ListNode* mergesort(vector& lists, int p, int r){
        if (preturn merge(mergesort(lists,p,(p+r)/2),mergesort(lists,(p+r)/2+1,r));
        else
            return lists[p];
    }
    ListNode* merge(ListNode* l1, ListNode* l2){
        if(l1 == NULL) return l2;
        if(l2 == NULL) return l1;

        ListNode* result = new ListNode(0);
        ListNode* head = result;
        while(l1 != NULL && l2 != NULL){
            if(l1->val < l2->val){
                head->next = new ListNode(l1->val);
                l1 = l1->next;
            }
            else{
                head->next  = new ListNode(l2->val);
                l2 = l2->next;
                }
            head = head->next; 
        }
        if(l1 == NULL)
            head->next = l2;
        else if(l2 == NULL)
            head->next = l1;
        return result->next;
    }
};

　　直接使用归并排序，每次都选择分割两个序列，算法负责度可以写作 T(n)=2T(n/2)+O(n) ，即 T(n)=O(nlogn) 。

　　总结：其实这周实现的算法都不是很难，但是可能我更多的时间都花在了怎么去优化它们了，最开始总是有先入为主的想法，分治一定会比较快，但其实不尽然（当然也有可能是我想的分治法比较麻烦==）。总之，我觉得这周选择的题目不仅刚好把课上学到的分治法的分析思想用上了，也让我学着去思考优化的问题，感觉收获颇多，接下来还是要好好刷题^^