斯坦福机器学习笔记（三）—— 高斯判别分析

概述

本篇博客主要是网易公开课上吴恩达教授讲解的机器学习视频中关于高斯判别分析的相关内容（网址为：http://open.163.com/movie/2008/1/A/R/M6SGF6VB4_M6SGHMFAR.html）。
视频中主要讲解了两种生成学习算法——高斯判别分析（GDA）和朴素贝叶斯（NB）。但是自己即将学习语音识别，组要设计高斯混合标模型、隐马尔科夫模型等。因此英文讲义上的朴素贝叶斯和拉普拉斯平滑的内容计算和视频第六讲讲义合在一起。**在这篇博客中主要是第原版英文讲义的翻译，但也补充了原文中省略推导过程的数学公式。**同时，为方便阅读，我已经将博客相关内容pdf文件上传CSDN了，如有需要移步：斯坦福机器学习笔记（三）—— 高斯判别分析（GDA）。高斯判别分析（GDA）的Python代码请移步：高斯判别分析（GDA）Python代码

在去年这个篇博客设置成私密文章，期间CSDN的Markdown经历的改版，不支持原来语法，使得大部分Latex数学公式无法显示，此前忙于考试故没有时间进行重新排版。

---

前记

到目前为止，我们主要讨论了对$p\left(y|x;\theta \right)$建模的学习算法，即给定$x$ 的$y$的条件分布。 例如，Logistic回归将$p\left(y|x;\theta \right)$ 建模为 $h_{\theta }\left(x\right)\text{= }g\left({\theta }^{T}x\right)$，其中$g$是Sigmoid函数。 在这份笔记中，我们将讨论一种不同类型的学习算法。
考虑一个分类问题，我们希望根据动物的某些特征来学习区分大象$\left(y=0\right)$ 和狗$\left(y=1\right)$ 。 给定训练集，像Logistic回归或基本感知器算法之类算法试图找到一条决定边界的直线，从而将大象和狗分开。然后，为了将新动物分类为大象或狗，该算法检查这个样本落在边界的哪一侧，并相应地进行预测。
现在介绍一种不同的方法。首先，看大象，我们可以建立一个大象样子的模型。 然后，看着狗，我们也可以单独建立一个狗的样子的模型。最后，为了对新动物进行分类，我们可以将新动物与大象模型相匹配，并将其与狗模型相匹配，以查看新动物是更像我们在训练集中看到的大象还是狗。
尝试直接学习$p\left(y|x\right)$的算法（例如逻辑回归），或试图学习直接将输入$X$ 的空间映射到标签$\left\{0,1\right\}$的算法（例如感知器算法）是称为判别学习算法。 在这里，我们将讨论算法，而是试图直接对$p\left(x|y\right)$ （和$p\left(y\right)$）建模。这些算法称为生成学习算法。 例如，如果$y$指示样本是狗（0）还是大象（1），则$p\left(x|y\text{=}0\right)$ 对狗的特征的分布进行建模，并且$p\left(x|y\text{=}1\right)$ 对大象特征的分布进行建模。
在对$p\left(y\right)$ 称为类先验）和$p\left(x|y\right)$ 进行建模之后，我们的算法可以使用贝叶斯规则在给定 $x$的$y$ 上推导出后验分布：
$$p\left(y|x\right)=\frac{p\left(x|y\right)p\left(y\right)}{p\left(x\right)}$$
这里分母为：$p\left(x\right)\text{=}p\left(x|y\text{=}1\right)p\left(y\text{=}1\right)\text{+}p\left(x|y\text{=}0\right)p\left(y\text{=}0\right)$ ，因此也可以用我们学到的量$p\left(x|y\right)$ 和 $p\left(y\right)$表示。 实际上，如果为了进行预测而计算$p\left(y|x\right)$ ，那么我们实际上并不需要计算分母，因为：
$$arg\underset{y}{\max }p\left(y|x\right)=arg\underset{y}{\max }\frac{p\left(x|y\right)p\left(y\right)}{p\left(x\right)}\text{=}arg\underset{y}{\max }p\left(x|y\right)p\left(y\right)$$
其中$p\left(y\right)$服从均匀分布，即$p\left(y\text{=}0\right)\text{=}p\left(y\text{=}1\right)$。

---

一 高斯判别分析

我们将看到的第一个生成学习算法是高斯判别分析（GDA）。在这个模型中，我们假设$p\left(x|y\right)$ 是服从多元正态分布分布。在继续讨论GDA之前，让我们简单地谈谈多元正态分布的性质。

1.1 多元正态分布

$n$ 维的多元正态分布，也称为多元高斯分布，均值向量$\mu \in {\mathbb{R}}^n$ ，协方差矩阵$\sum \in {\mathbb{R}}^{n\times n}$,其中 $\sum \ge 0$， 即是半正定对称矩阵。多元高斯分布也写成$N\left(\mu ,\sum \right)$ ，其概率密度如下：
$$p\left(x;\mu ,\sum \right)=\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}{\left|\sum \right|}^{\frac{1}{2}}}\exp \left(\text{-}\frac{1}{2}{\left(x-\mu \right)}^T{\sum }^{\text{-}1}\left(x-\mu \right)\right)$$

在上面的等式中，$\left|\sum \right|$表示矩阵$\sum$的行列式。对于服从$N\left(\mu ,\sum \right)$ 的随机变量 $X$，均值由$\mu$给出：

$$E\left(X\right)={\int }_{x}xp\left(x;\mu ,\sum \right)dx=\mu$$

同时，向量值随机变量$Z$ 的协方差定义为：
$$Cov\left(Z\right)=E\left[\left(Z-E\left[Z\right]\right){\left(Z-E\left[Z\right]\right)}^T\right]$$

这也描述了实随机变量方差的概念。协方差也可以定义为：
$$Cov\left(\mathrm{Z}\right)=E\left[\mathrm{Z}{\mathrm{Z}}^T\right]-\left(E\left[Z\right]\right){\left(E\left[Z\right]\right)}^T$$

如果 $X\sim N\left(\mu ,\sum \right)$，那么： $Cov\left(Z\right)\text{=}\sum$

以下是高斯分布密度的一些示例。上图最左边的图显示了一个均值为零（即$2\times 1$ 零向量）和协方差矩阵$\sum =I$ （ $2\times 2$单位矩阵）的高斯分布，这样的高斯分布也称为标准正态分布。中间的图显示的为零均值和 $\sum =0.6I$的高斯分布。在最右边的图中显示为零均值和$\sum =2I$ 。我们看到随着 变大，高斯变得更加“展开”（“矮胖”）。随着它变小，分布变得更加“压缩”（“瘦高”）。

让我们看一些更多的例子。下图显示高斯分布的均值为0，协方差矩阵依次分别为：

$$\begin{array}{ccc}\sum \text{=}\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)& \sum \text{=}\left(\begin{array}{cc}1& 0.5\\ 0.5& 1\end{array}\right)& \sum \text{=}\left(\begin{array}{cc}1& 0.8\\ 0.8& 1\end{array}\right)\end{array}$$

最左边的图显示了熟悉的标准正态分布，我们看到随着$\sum $ 非对角线条目的增加，其概率密度更加“压缩”了${45}^{\circ }$ 。当我们处于相同的三个密度的轮廓时，我们可以更清楚地看到这一点：

下面是通过改变$\sum$ 生成的最后一组示例：

上面的图分别使用了如下协方差矩阵：
$$\begin{array}{ccc}\sum \text{=}\left(\begin{array}{cc}1& \text{-}0.5\\ \text{-}0.5& 1\end{array}\right)& \sum \text{=}\left(\begin{array}{cc}1& \text{-}0.8\\ \text{-}0.8& 1\end{array}\right)& \sum \text{=}\left(\begin{array}{cc}3& 0.8\\ 0.8& 1\end{array}\right)\end{array}$$

从最左边和中间的图可以看出，我们看到通过减少协方差矩阵对角线的元素，密度在此变得更“压缩”，但方向相反。最后，随着我们改变参数，更多一般来说，轮廓将形成椭圆形（最右边的图形显示一个椭圆形例子）。

作为我们的最后一组示例，通过改变$\mu$ 来固定 $\sum \text{=}I$，我们也可以移概率动密度的平均值。上图用$\sum \text{=}I$生成，同时个图对应的协方差矩阵如下：
$$\begin{array}{ccc}\mu \text{=}\left(\begin{array}{c}1\\ 0\end{array}\right)& \mu \text{=}\left(\begin{array}{c}\text{-}0.5\\ 0\end{array}\right)& \mu \text{=}\left(\begin{array}{c}\text{-}1\\ \text{-}1.5\end{array}\right)\end{array}$$

1.2 高斯判别分析模型

当我们有一个输入特征 是连续随机变量的分类问题时，我们可以使用高斯判别分析（GDA）模型，该模型使用多元正态分布对$p\left(x|y\right)$ 进行建模。这个模型如下：

$$\begin{array}{c}y\sim Bernoulli\left(\varphi \right)\\ x|y=0\sim N\left({\mu }_0,\sum \right)\\ x|y=1\sim N\left({\mu }_1,\sum \right)\end{array}$$

其中， $Bernoulli\left(\varphi \right)$表示的伯努利分布，即0-1分布或者二项分布。那么有：
$$\begin{array}{c}p\left(y\right)={\varphi }^y{\left(1-\varphi \right)}^{1-y}\\ p\left(x|y=0\right)=\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}{|\sum |}^{\frac{1}{2}}}\exp \left(\text{-}\frac{1}{2}{\left(x-{\mu }_0\right)}^T{\sum }^{\text{-}1}\left(x-{\mu }_0\right)\right)\\ p\left(x|y=1\right)=\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}{|\sum |}^{\frac{1}{2}}}\exp \left(\text{-}\frac{1}{2}{\left(x-{\mu }_1\right)}^T{\sum }^{\text{-}1}\left(x-{\mu }_1\right)\right)\end{array}$$

这里，我们模型的参数是 $\phi $，$\sum $ ，${\mu }_0$和${\mu }_1$ （注意，虽然有两个不同的均值向量${\mu }_0$和${\mu }_1$ ，但这个模型应用最多仅使用相同的协方差矩阵$\sum $ ，${\mu }_0$和${\mu }_1$ （注意，虽然有两个不同的均值向量${{\mu ）。对于给定数据的对数似然函数如下：
$$\begin{array}{rl}\ell \left(\varphi ,{\mu }_0,{\mu }_1,\Sigma \right)& =\log \prod _{i=1}^{m}p\left(x^{(i)},y^{(i)};{\mu }_0,{\mu }_1,\Sigma \right)\\ & =\log \prod _{i=1}^{m}p\left(x^{(i)}|y^{(i)};{\mu }_0,{\mu }_1,\Sigma \right)p\left(y^{(i)};\varphi \right)\\ & =\sum _{i=1}^m\log p\left(x^{(i)}|y^{(i)};{\mu }_0,{\mu }_1,\Sigma \right)+\sum _{i=1}^m\log p\left(y^{(i)};\varphi \right)\\ & =\sum _{i=1}^m{y}^{(i)}\log p\left(x^{(i)}|y^{(i)}=1;{\mu }_0,{\mu }_1,\Sigma \right)+\sum _{i=1}^m\log p\left(y^{(i)};\varphi \right)\\ & +\sum _{i=1}^m{y}^{(i)}\log p\left(x^{(i)}|y^{(i)}=0;{\mu }_0,{\mu }_1,\Sigma \right)+\sum _{i=1}^m\log p\left(y^{(i)};\varphi \right)\end{array}$$

那么，结合式(1)对 求偏导有：
$$\begin{array}{rl}\frac{\partial \ell }{\partial \varphi }& =\frac{\partial }{\partial \varphi }\left(\sum _{i=1}^m\log p\left(y^{(i)};\varphi \right)\right)\\ & =\frac{\partial }{\partial \varphi }\left(\sum _{i=1}^m\log p\left(y^{(i)};\varphi \right)\right)\\ & =\frac{\partial }{\partial \varphi }{\left(\sum _{i=1}^m\log {\varphi }^{\prime \prime \prime }(1-y{)}^{1-y^{\prime \prime }}\right)}^{1-y^{\prime \prime }})\\ & =\frac{\partial }{\partial \varphi }{\left(\sum _{i=1}^m\left[y^{(i)}\log \varphi +\left(1-y^{(i)}\right)\log (1-\varphi )\right]\right)}^{\prime }\\ & =\frac{\partial }{\partial \varphi }{\left(\sum _{i=1}^m\left[y^{(i)}\log \varphi +\left(1-y^{(i)}\right)\log (1-\varphi )\right]\right)}^{\prime }\\ & =\frac{{\sum }_{i=1}^m{y}^{(i)}}{\varphi }-\frac{{\sum }_{i=1}^m\left(1-y^{(i)}\right)}{1-\varphi }\end{array}$$

令$\frac{\partial \ell }{\partial \varphi }\text{=}0$ ，我们可以得到：
$$\varphi \text{=}\frac{1}{m}\sum _{i=1}^{m}1\left\{y^{\left(i\right)}=1\right\}$$

同理有：
$$\begin{array}{rl}\frac{\partial \ell }{\partial u_0}& =\frac{\partial }{\partial u_0}\left[\sum _{i=1}^m\left(1-y^{(i)}\right)\log p\left(x^{(i)}|y^{(i)}=0;{\mu }_0,{\mu }_1,\Sigma \right)\right]\\ & =\frac{\partial }{\partial u_0}\left[\sum _{i=1}^m\left(1-y^{(i)}\right)\log \frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp \left(-\frac{1}{2}{\left(x^{(i)}-{\mu }_0\right)}^T{\Sigma }^{-1}\left(x^{(i)}-{\mu }_0\right)\right)\right]\\ & =\sum _{i=1}^m\left(1-y^{(i)}\right){\Sigma }^{-1}\left(x^{(i)}-{\mu }_0\right)=0\end{array}$$

由于$\sum$ 是对称矩阵，那么有：
$$\sum _{i=1}^m\left(1-y^{(i)}\right)\left(x^{(i)}-{\mu }_0\right)=\sum _{i=1}^m{\left(1-y^{(i)}\right)}^{(i)}-\sum _{i=1}^m\left(1-y^{(i)}\right){\mu }_0=0$$

计算求得：
$${\mu }_0=\frac{{\sum }_{i=1}^{m}1\left\{y^{(i)}=0\right\}{x}^{(i)}}{{\sum }_{i=1}^{m}1\left\{y^{(i)}=0\right\}}$$

同理可得：
$${\mu }_1=\frac{{\sum }_{i=1}^{m}1\left\{y^{(i)}=1\right\}{x}^{(i)}}{{\sum }_{i=1}^{m}1\left\{y^{(i)}=1\right\}}$$

对于协方差矩阵$\sum$ 而言，我们有如下公式：
$$\{\begin{array}{l}\frac{\partial |\Sigma |}{\partial \Sigma }=|\Sigma |{\Sigma }^{-1}\\ \frac{\partial {\Sigma }^{-1}}{\partial \Sigma }=-{\Sigma }^2\end{array}$$

那么我们有：
$$\begin{gathered} \sum _{i=1}^m{y}^{(i)}\log p\left(x^{(i)}|y^{(i)}=1;{\mu }_0,{\mu }_1,\Sigma \right)+\sum _{i=1}^m\left(1-y^{(i)}\right)\log p\left(x^{(i)}|y^{(i)}=0;{\mu }_0,{\mu }_1,\Sigma \right) \\ =\sum _{i=1}^m{y}^{(i)}\log \frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp \left(-\frac{1}{2}{\left(x^{(i)}-{\mu }_1\right)}^T{\Sigma }^{-1}\left(x^{(i)}-{\mu }_1\right)\right) \\ +\sum _{i=1}^m\left[1-y^{(i)}\right)\log \frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp \left(-\frac{1}{2}{\left(x^{(i)}-{\mu }_0\right)}^T{\Sigma }^{-1}\left(x^{(i)}-{\mu }_0\right)\right) \\ =\sum _{i=1}^m\left[-\frac{n}{2}\log 2\pi -\frac{1}{2}\log |\Sigma |\right]-\frac{1}{2}\sum _{i=1}^m{\left(x^{(i)}-{\mu }_{y^{(i)}}\right)}^T{\Sigma }^{-1}\left(x^{(i)}-{\mu }_{y^{(i)}}\right) \end{gathered}$$

那么结合式(2)，对$\sum$ 求偏导有：
$$\frac{\partial \ell }{\partial \sum }=-\frac{m}{2}{\Sigma }^{-1}+\frac{{\sum }^{-2}}{2}\sum _{i=1}^m\left(x^{(i)}-{\mu }_{y^{(i)}}\right){\left(x^{(i)}-{\mu }_{y^{(i)}}\right)}^T=0$$

那么有：
$$\Sigma =\frac{1}{m}\sum _{i=1}^m\left(x^{(i)}-{\mu }_{y^{(i)}}\right){\left(x^{(i)}-{\mu }_{y^{(i)}}\right)}^T$$

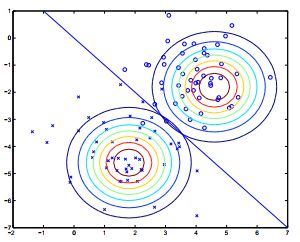
从图中可以看出，高斯判别分析（GDA）算法的作用如下：

图中显示的是训练集，以及两个高斯分布的轮廓，这两个高斯分布已经适合两个类中的每个类中的数据。注意，两个高斯的轮廓虽然具有相同的形状和方向，在是因为它们共享协方差矩阵$\sum$ ，但它们具有不同的均值${\mu }_{\text{0}}$和${\mu }_{\text{1}}$ 。图中还给出决策边界的直线，在这条直线上$p\left(y=1|x\right)=0.5$ 。在边界的一侧，我们预测$y=1$ 是最可能的结果，而另一方面，我们预测$y=0$。

1.3 讨论：GDA与Logistic回归

GDA模型与Logistic回归有着有趣的关系。如果我们将$p\left(y=1|x;\varphi ,{\mu }_0,{\mu }_1,\sum \right)$ 视为$x$的函数，我们会发现它可以表示为：
$$\begin{array}{rl}& p\left(y=1|x;\varphi ,{\mu }_0,{\mu }_1,\sum \right)=\frac{p\left(x|y=1;\varphi ,{\mu }_0,{\mu }_1,\sum \right)p\left(y=1\right)}{p\left(x|y=1;\varphi ,{\mu }_0,{\mu }_1,\sum \right)p\left(y=1\right)+p\left(x|y=0;\varphi ,{\mu }_0,{\mu }_1,\sum \right)p\left(y=0\right)}\\ & =\frac{\frac{\varphi }{{\left(2\pi \right)}^{\frac{n}{2}}{|\sum |}^{\frac{1}{2}}}\exp \left(\text{-}\frac{1}{2}{\left(x-{\mu }_1\right)}^T{\sum }^{\text{-}1}\left(x-{\mu }_1\right)\right)}{\frac{\varphi }{{\left(2\pi \right)}^{\frac{n}{2}}{|\sum |}^{\frac{1}{2}}}\exp \left(\text{-}\frac{1}{2}{\left(x-{\mu }_1\right)}^T{\sum }^{\text{-}1}\left(x-{\mu }_1\right)\right)+\frac{1-\varphi }{{\left(2\pi \right)}^{\frac{n}{2}}{|\sum |}^{\frac{1}{2}}}\exp \left(\text{-}\frac{1}{2}{\left(x-{\mu }_0\right)}^T{\sum }^{\text{-}1}\left(x-{\mu }_0\right)\right)}\\ & =\frac{1}{1+\frac{1-\varphi }{\varphi }\exp \left[\text{-}\frac{1}{2}\left({\mu }_0^T{\sum }^{-1}{\mu }_0-{\mu }_1^T{\sum }^{-1}{\mu }_1\right)+\left({\mu }_0-{\mu }_1\right){\sum }^{-1}x\right]}\\ & =\frac{1}{1+\exp \left[\text{-}\frac{1}{2}\left({\mu }_0^T{\sum }^{-1}{\mu }_0-{\mu }_1^T{\sum }^{-1}{\mu }_1\right)+\log \frac{1-\varphi }{\varphi }-\left({\mu }_1-{\mu }_0\right){\sum }^{-1}x\right]}\\ & =\frac{1}{1+\exp \left(-{\theta }^{T}x\right)}\end{array}$$

其中，
$$\{\begin{array}{c}\left({\mu }_1-{\mu }_0\right){\Sigma }^{-1}=\left({\theta }_1,\cdots ,{\theta }_m\right)\\ -\frac{1}{2}\left({\mu }_0^T{\Sigma }^{-1}{\mu }_0-{\mu }_1^T{\Sigma }^{-1}{\mu }_1\right)+\log \frac{1-\varphi }{\varphi }={\theta }_0\end{array}$$
同时在这里， $p\left(x|y\right)$是条件概率，$p\left(y\right)$是先验概率， $p\left(y|x\right)$是后验概率。

什么时候比起其中一种模型，我们更偏向用另一种模型？一般而言，利用相同的数据集进行训练后，GDA和Logistic回归会给出不同的决策边界。哪个更好呢？

我们认为如果$p\left(x|y\right)$ 服从多元高斯分布（相同的 ），那么$p\left(y|x\right)$ 必然遵循Logistic函数。然而，相反的情况并非如此；即 $p\left(y|x\right)$是Logistic函数并不意味着 $p\left(x|y\right)$服从多元高斯分布。这表明GDA比Logistic回归对数据做出更强的建模假设。事实证明，当这些建模假设正确时，GDA将找到更好的数据拟合，并且是更好的模型。具体来说，当$p\left(x|y\right)$ 确实服从是多元高斯（具有相同$\sum$ ）时，则GDA是渐近有效的。非正式地说，这意味着在非常大的训练集（大$m$）的极限中，没有比GDA严格更好的算法（就他们估计 的准确程度而言）。 特别是可以证明，在这种情况下，GDA将是一种比Logistic回归更好的算法; 更一般地说，即使是小型训练集，GDA的效果也更好。

相反，通过做出明显较弱的假设，逻辑回归也更加具有鲁棒性，对不正确的建模假设也不那么敏感。有许多不同的假设会导致$p\left(y|x\right)$采用逻辑函数的形式。 例如，如果$x|y=0\sim Poisson\left({\lambda }_0\right)$ ，并且$x|y=1\sim Poisson\left({\lambda }_1\right)$，那么$p\left(y|x\right)$将是Logisti函数形式。 Logistic回归也可以很好地处理像这样服从Poisson分布的数据。但是如果我们在这样的数据上使用GDA并且将高斯分布拟合到这样的非高斯分布数据，那么结果将是不太可预测的，并且GDA可能（或可能不）表现良好。

总而言之：当建模假设正确或至少近似正确时，GDA做出更强的建模假设，并且有更多有效的数据时效果比Logistic回归好（即，只需更少的训练数据来“好”学习）。Logistic回归假设较弱，而且对建模假设要求不高，具有更好的鲁棒性。具体来说，当数据不服从高斯分布时，那么在大数据集下，Logistic回归几乎总是比GDA更好，更具有鲁棒性。 因此在实践中，Logistic回归比GDA更常用。

---

个人理解，根据大数定律，当数据量极大时，数据将会无限逼近高斯分布，这时GDA将比Logistic回归效果更好。从某种程度上说，GDA可以看成是Logistic回归在数据服从在高斯分布时的一个特例，而Logistic回归则使用任何数据集，不管数据是否服从高斯分布，Logistic回归是GDA的一个推广。