Agglomerative Hierarchical Clustering详解
Agglomerative Hierarchical Clustering详解
第二十七次写博客,本人数学基础不是太好,如果有幸能得到读者指正,感激不尽,希望能借此机会向大家学习。这一篇文章主要是介绍各种凝聚层次聚类(Agglomerative Hierarchical Clustering)技术,从基本凝聚层次聚类算法出发,介绍了该类算法中各种“距离”的定义以及时间、空间复杂度,然后介绍了各种不同的“距离”定义对聚类结果的影响,最后介绍了一种具体的凝聚层次聚类实现算法(AGNES)。
凝聚层次聚类
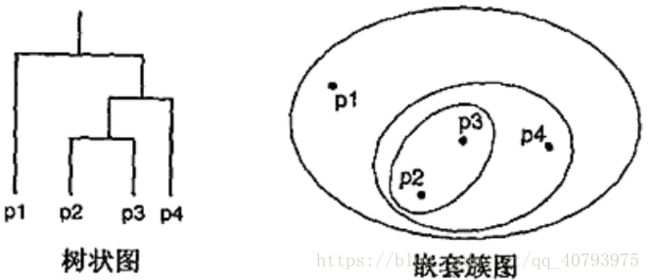
凝聚层次聚类先将每个样本点作为一个个体簇,然后每一步合并两个“距离”最近的簇,这里的距离可以看做是簇邻近性的定义,这在下文 “MIN、MAX与组平均”中会讲到。层次聚类常常使用树状图(dendrogram)来表示(如图1,采用“单链”聚类),从图中可以清楚的看出簇与其子簇之间的关系,以及簇合并与分裂的次序。对于二维样本点来说,还可以使用类似嵌套簇图(Nested Cluster Diagram)的方式来表示。
基本凝聚层次聚类
基本凝聚层次聚类是该聚类算法族的基础,其主体思想是,从个体点作为簇开始,相继合并两个“距离”最近的簇,直到只剩下一个簇,具体步骤如下图所示
层次聚类中的“距离”定义
由上述讨论可知,凝聚层次聚类的关键是两个簇之间“距离”的度量方法,这里的“距离”也可以成为“邻近度”,许多凝聚层次聚类技术的“距离”定义都源于基于图的观点,例如下面要讲的MIN、MAX与组平均距离(如图3所示)。
MIN(最小距离):不同簇之间的两个最近点之间的邻近度,使用图的术语可以表示为,不同结点子集之间的最短边长;
MAX(最大距离):不同簇之间的两个最远点之间的邻近度,使用图的术语可以表示为,不同结点子集之间的最长边长;
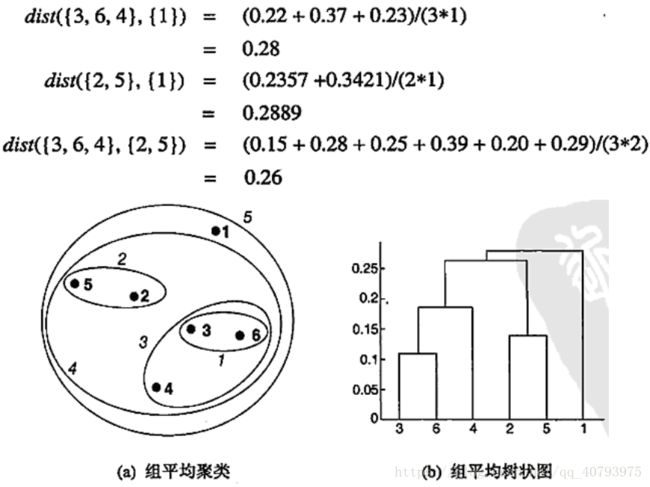
(组)平均距离:不同簇之间的所有点对之间的邻近度的平均值,使用图的术语可以表示为,不同结点子集之间的平均边长。
另外,两个簇质心之间的距离也可以作为邻近度度量的条件,实际上类似于K-Means算法在进行后处理中对两个质心最近的簇进行合并的思想。
时间复杂度与空间复杂度
图2算法伪代码的第一行指出为了存储邻近度矩阵需要的空间复杂度是 O ( m 2 ) O\left(m^2\right) O(m2),在得到最终结果之前需要进行 m − 1 m-1 m−1次迭代,每次迭代需要计算每个簇之间的邻近度矩阵,每次迭代的时间复杂度为 O ( ( m − i + 1 ) 2 ) O\left(\left(m-i+1\right)^2\right) O((m−i+1)2),如果对基本层次聚类算法不进行任何修改,那么该算法的时间复杂度将达到 O ( m 3 ) O\left(m^3\right) O(m3),即使将某个簇与其他簇之间的距离保存在一个数组或者一个堆之中,也需要 O ( m 2 log m ) O\left(m^2\log{m}\right) O(m2logm)的时间复杂度。因此,层次聚类的复杂度严重的限制了其适用的数据集大小。
MIN、MAX、组平均与质心距离
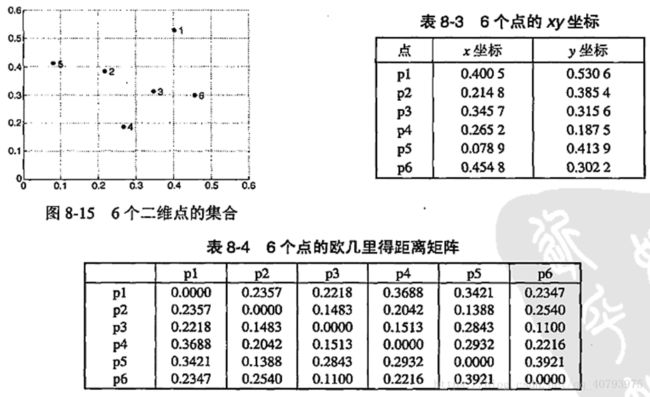
假设存在一个包含6个样本的二维数据集,这里采用欧氏距离来表示邻近度,这些样本点在坐标系中的位置以及每个点之间的邻近度矩阵如下图所示
下面分别基于MIN、MAX、组平均以及质心距离来讨论不同的簇间距离度量方式对最终聚类效果的影响,然后给出一个用于计算邻近度的通用公式,即Lance-Williams公式。
MIN
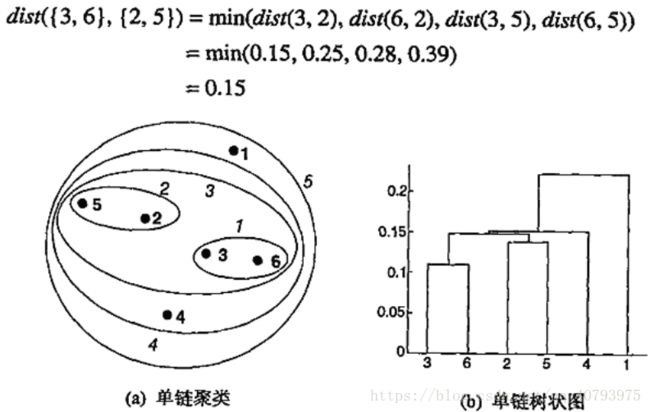
MIN又称为“单链”,即不同簇之间的两个最近点之间的邻近度,使用图的术语可以表示为,不同结点子集之间的最短边长(最大邻近度)。从所有点作为单点簇开始,每次在两个簇的最近点之间增加一条链,先加最短的链,这些链将节点子集合并成为簇,簇 C i C_i Ci和 C j C_j Cj之间的组平均距离可以通过下式进行计算
(1) p r o x i m i t y ( C i , C j ) = min x ∈ C i , y ∈ C j p r o x i m i t y ( x , y ) proximity\left(C_i,C_j\right) =\min_{\mathbf{x}\in{C_{i}},\mathbf{y}\in{C_{j}}}{proximity\left(\mathbf{x},\mathbf{y}\right)} \tag{1} proximity(Ci,Cj)=x∈Ci,y∈Cjminproximity(x,y)(1)
树状图和嵌套簇图如下图所示
单链技术适合处理非椭圆形状的簇,但是对于噪声和离群点十分敏感。
MAX
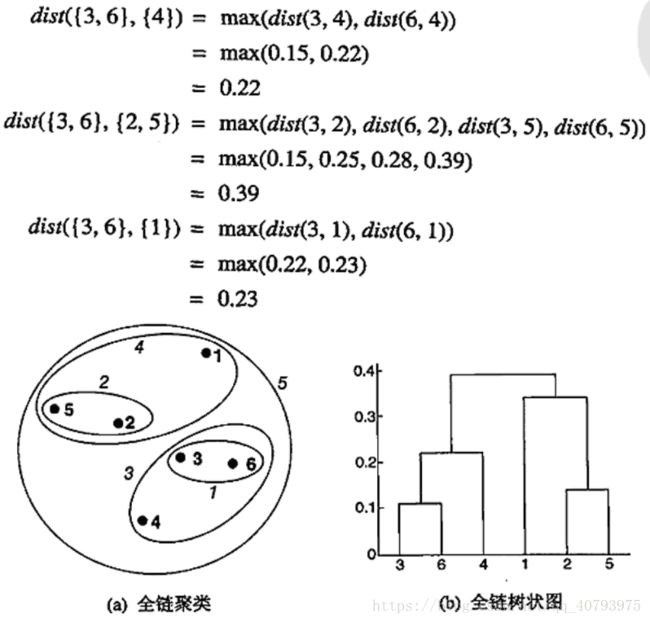
MAX又称为“全链”或“团”,即不同簇之间的两个最远点之间的邻近度,使用图的术语可以表示为,不同结点子集之间的最长边长(最小邻近度)。从所有点作为单点簇开始,每次在两个簇的最远点之间增加一条链,先加最短的链,这些链将节点子集连接成为一个簇(团),簇 C i C_i Ci和 C j C_j Cj之间的组平均距离可以通过下式进行计算
(2) p r o x i m i t y ( C i , C j ) = max x ∈ C i , y ∈ C j p r o x i m i t y ( x , y ) proximity\left(C_i,C_j\right) =\max_{\mathbf{x}\in{C_{i}},\mathbf{y}\in{C_{j}}}{proximity\left(\mathbf{x},\mathbf{y}\right)} \tag{2} proximity(Ci,Cj)=x∈Ci,y∈Cjmaxproximity(x,y)(2)
树状图和嵌套簇图如下图所示
全链技术生成的簇形状偏向于圆形,且不易受到噪声和离群点的影响,但是容易使大的簇破裂。
组平均
组平均,即不同簇之间的所有点对之间的邻近度的平均值,使用图的术语可以表示为,不同结点子集之间的平均边长,这是一种单链与全链之间折中的方法,簇 C i C_i Ci和 C j C_j Cj之间的组平均距离可以通过下式进行计算
(3) p r o x i m i t y ( C i , C j ) = ∑ x ∈ C i , y ∈ C j p r o x i m i t y ( x , y ) m i , m j proximity\left(C_i,C_j\right) =\frac{\sum_{\mathbf{x}\in{C_{i}},\mathbf{y}\in{C_{j}}}{proximity\left(\mathbf{x},\mathbf{y}\right)}}{m_i,m_j} \tag{3} proximity(Ci,Cj)=mi,mj∑x∈Ci,y∈Cjproximity(x,y)(3)
树状图和嵌套簇图如下图所示
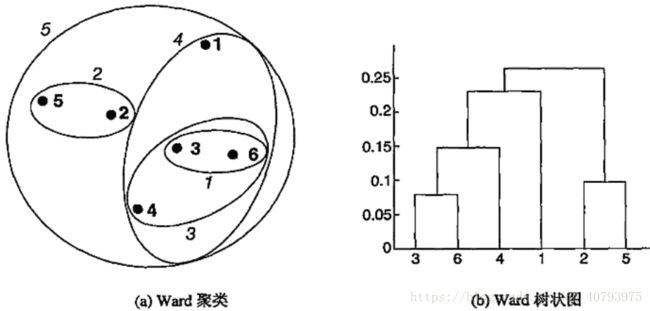
与组平均类似的ward方法,选择可以使总体SSE增加最小的两个簇进行合并,虽然这种优化目标被用于K-Means的后处理中,但是当邻近度取两个样本点之间的距离平方时,可以在数学上证明,Ward方法与组平均非常相似。树状图和嵌套簇图如下图所示
质心距离
质心法通过计算两个簇的质心之间的距离来带表邻近度,质心法不同于其他层次聚类方法的重要一点是倒置(inversion)的可能,倒置是指这一轮合并的两个簇可能比上一轮合并的两个簇更为近似,而其他方法的邻近度均是单调增加或不变的。
Lance-Williams公式
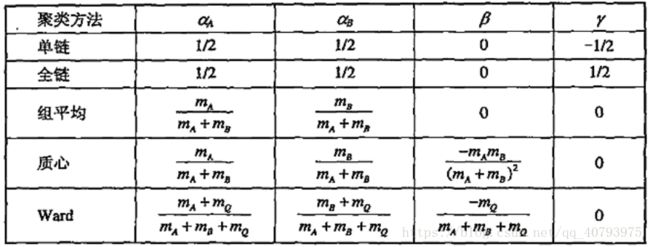
作为一种度量簇间邻近度的通用公式,Lance-Williams公式将以上讨论的四种度量方法作为可选参数,假设存在三个不同的簇 A A A、 B B B、 Q Q Q,簇 R R R是簇 A A A、 B B B合并之后产生的新簇,那么Lance-Williams公式可以表示为
(4) p ( R , Q ) = α A ∗ p ( A , Q ) + α B ∗ p ( B , Q ) + β ∗ p ( A , B ) + γ ∗ ∣ p ( A , Q ) − p ( B , Q ) ∣ p\left(R,Q\right)=\alpha_{A}*p\left(A,Q\right)+\alpha_{B}*p\left(B,Q\right)+{\beta}*p\left(A,B\right)+{\gamma}*|p\left(A,Q\right)-p\left(B,Q\right)| \tag{4} p(R,Q)=αA∗p(A,Q)+αB∗p(B,Q)+β∗p(A,B)+γ∗∣p(A,Q)−p(B,Q)∣(4)
具体来说,该公式将簇 A A A、 B B B合并后产生的新簇 R R R与 Q Q Q之间的邻近度转化成为簇 A A A与 Q Q Q、簇 B B B与 Q Q Q,以及簇 A A A与 B B B之间邻近度的线性函数。下图指出了不同邻近度度量函数所对应的系数( m m m是对应簇的样本点个数)
层次聚类的三个主要问题
缺乏全局目标函数
通过前面的讨论可知,层次聚类每一步都是局部的决定哪两个簇可以进行合并,即使是像以“最小化距离平方”为目标的Ward方法,在每步合并中也是基于当前SSE进行讨论的,而不是以全局SSE最小作为优化目标的。这种方法虽然使用这种简单的思想避开了复杂的交替组合优化问题,但是产生了局部最优的风险,另外,其时间复杂度与空间复杂度大大限制了其处理大规模数据的能力。
处理不同大小簇的能力
这里只针对于设计求和的簇临近性度量方案进行讨论,在合并两个不同大小的簇时,一般采用两种方法:加权与非加权。其中,加权方法将这两个待合并的簇中的每一个样本赋予相应的权值,而非加权的方法则要考虑簇的大小,并且为每个样本赋予相同的权值。
之前讨论过的组平均(式(3))就是非加权版本,该方法的全称是“算数平均的、非加权的对组方法”(Unweighted Pair Group Method using Arithmetic averages,UPGMA),他的加权版本称为WPGMA,它所对应的图8中的系数为: α A = α B = 1 / 2 , β = γ = 0 \alpha_{A}=\alpha_{B}=1/2,\beta=\gamma=0 αA=αB=1/2,β=γ=0,通常情况下非加权的版本更可靠,除非由于重采样等原因导致需要考虑样本权值时。
合并决策是最终的
对于合并两个簇,凝聚层次聚类算法趋向于做出好的局部决策,因为他们可以使用所有点的逐对相似度信息,然而,一旦做出合并两个簇的决策,以后就不能撤销。这种方法阻碍了局部最优标准转化成为全局最优标准。这与缺乏全局最优目标问题,可以同过先使用其他聚类算法(如K-Means)得到一些规模较小的簇,然后再用凝聚层次聚类算法对这些簇进一步聚类。
AGNES聚类
这里介绍一种凝聚层次聚类算法AGNES,其大体思想与图2所示的基本凝聚层次聚类算法类似,伪代码如下所示
算法第1-3行:将每个样本点初始化为单点簇;
算法第4-9行:初始化距离矩阵;
算法第10-23:迭代合并直到产生 k k k个簇。
参考资料
【1】《机器学习》周志华
【2】《数据挖掘导论》