ER模型
实体关系(ER)模型的目标是捕获现实世界的数据需求,并以简单、易理解的方式表现出来。ER模型可用于项目组内部交流或用于与用户讨论系统数据需求。
ER模型中的基本元素
基本的ER模型包含三类元素:实体、关系、属性
图1 实体、关系、属性的ER构图
实体(Entities):实体是首要的数据对象,常用于表示一个人、地方、某样事物或某个事件。一个特定的实体被称为实体实例(entity instance或entity occurrence)。实体用长方形框表示,实体的名称标识在框内。一般名称单词的首字母大写。
关系(Relationships):关系表示一个或多个实体之间的联系。关系依赖于实体,一般没有物理概念上的存在。关系最常用来表示实体之间,一对一,一对多,多对多的对应。关系的构图是一个菱形,关系的名称一般为动词。关系的端点联系着角色(role)。一般情况下角色名可以省略,因为实体名和关系名已经能清楚的反应角色的概念,但有些情况下我们需标出角色名来避免歧义。
属性(Attributes):属性为实体提供详细的描述信息。一个特定实体的某个属性被称为属性值。Employee实体的属性可能有:emp-id, emp-name, emp-address, phone-no……。属性一般以椭圆形表示,并与描述的实体连接。属性可被分为两类:标识符(identifiers),描述符(descriptors)。Identifiers可以唯一标识实体的一个实例(key),可以由多个属性组成。ER图中通过在属性名下加上下划线来标识。多值属性(multivalued attributes)用两条线与实体连接,eg:hobbies属性(一个人可能有多个hobby,如reading,movies…)。复合属性(Complex attributes)本身还有其它属性。
辨别强实体与弱实体:强实体内部有唯一的标识符。弱实体(weak entities)的标识符来自于一个或多个其它强实体。弱实体用双线长方形框表示,依赖于强实体而存在。
深入理解关系
关系在ER模型中扮演了非常重要的角色。通过ER图可以描述实体间关系的度、连通数、存在性信息。
我们一一来解释这些概念。首先我们来看一下关系在ER图中的各种语义。
图2 关系的度、连通数、存在性
关系的度(Degree of a Relationship)
表示关系所关联的实体数量。二元关系与三元关系的度分别为2和3,以此可以类推至n元。二元关系是最常见的关系。
一个Employee与另一个Employee之间的领导关系称为二元回归关系。如图2中所示,Employee实体通过关系manages与自身连接。由于Employee在这一关系中扮演两个角色,故标出了角色名(manager和subordinate)。
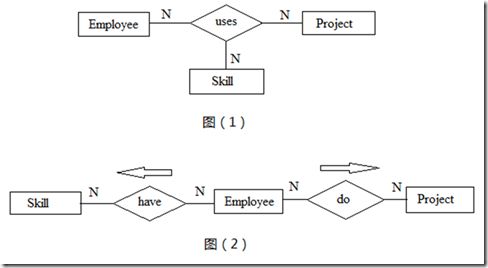
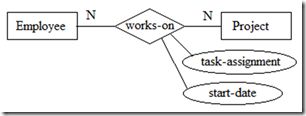
三元关系联系三个实体。当二元关系无法准确描述关联的语义时,就需要使用三元关系。我们来看下面这个例子,下图(1)能反映出一个Employee在某个Project中使用了什么Skill。下图(2)只能看出Employee有什么Skill,参与了哪些Project,但无法知道在某个Project中使用的特定Skill。
图3 三元关系蕴含的语义
需要注意的是有些情况下会错误的定义三元关系。这些三元关系可分解为2个或3个二元关系,来达到化简与语义的纯净。以后的博文中会进一步详细讨论三元关系。
一个实体可以参与到任意多个关系中。每个关系可以联系任意多个元(实体),而且两个实体之间也能有任意多个二元关系。
关系的连通数(Connectivity of a Relationship)
表示关系所关联的实例数量的约束。
连通数的值可以是“一”或“多”。“一”这一端,在ER图中通过在实体与关系间标记“1”表示。“多”一端标记“N”表示。如图2中关系连通数部分,“一”对“一”:Department is managed by Employee;“一”对“多”:Department has Employees;“多”对“多”:Employee may work on many Projects and each Project may have many Employees。
有些情况下最大连通数是确定的,可以用数值代替N。如:田径队队员有12人。
关系的属性
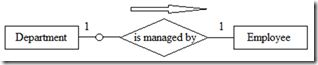
关系也能有属性。如下图4所示,某员工参与某项目的起始日期,某员工在某项目中被分配的任务只有放在关系works-on上才有意义。
图4 关系的属性
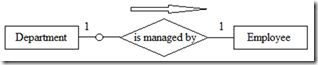
需要注意的是关系的属性一般出现在“多”对“多”的二元关系或三元关系上。一般“一”对“一”或“一”对“多”关系上不会放属性(会引起歧义)。而且这些属性可以移至一端的实体中。如下图5所示,如果部门与员工(经理)之间是“一”对“一”关系,在建模中可能把start-date作为关系is managed by的属性(表示被接管的时间),这个属性可以移至Department或Employee实体中。
图5 部门与经理之间的一对一管理关系
大家可以思考一下如果部门和经理之间是“多”对“多”关系,即交叉管理,那又会怎样?
关系中实体的存在性(Existence of an Entity in a Relationship)
关系中实体的存在性可以是强制的或可选的。当关系中的某一边实体(无论是“一”或“多”端)必须总是存在,则该实体为强制的。反之,该实体为可选的。
在实体与关系之间的连接线上标识“0”来表示可选存在性。含义是最小连通数为0。
强制存在性表示最小连通数为1。在存在性不确定或不可知的情况下,默认最小连通数为1。
在ER图中最大连通数显式地标识在实体旁边。如图6所示,其蕴含的语义为一个Department有且只有一个Employee来当经理,一个Employee可能是一个Department的经理,也可能不是。
图6 关系中实体的存在性
其他概念数据模型标记法
前文中使用的ER构图方法是Peter Chen 1976年提出的。在现代数据库设计领域,还有其他多种ER模型标记法。
我们来看一下另一种使用较多的标记法,“crow’s-foot”(鱼尾纹)标记法,并与前面介绍的标记法进行一个简单对比。
学习每一种标记法没有意义。在你的组织中推广应用一种标记法,使其成为大家共通的“语言”。
图7 Chen式标记法与crow’s-foot标记法对照
以下为高级ER模型构件:
泛化(Generalization):超类型与子类型
原始的ER模型已经能描述基本的数据和关系,但泛化(Generalization)概念的引入能方便多个概念数据模型的集成。
泛化关系是指抽取多个实体的共同属性作为超类实体。泛化层次关系中的低层次实体——子类型,对超类实体中的属性进行继承与添加,子类型特殊化了超类型。
ER模型中的泛化与面向对象编程中的继承概念相似,但其标记法(构图方式)有些差异。
下图表示员工与经理、工程师、技术员、秘书之间的泛化关系。Employee为超类实体,并包含共同属性,Manager、Engineer、Technician、Secretary都是Employee的子类实体,它们能包含自身特有的属性。
图1 Employee与Manager、Engineer、Technician、Secretary之间的泛化关系
泛化可以表达子类型的两种重要约束,重叠性约束(disjointness)与完备性约束(completeness)。
重叠性约束表示各个子类型之间是否是排他的。若为排他的则用字母“d”标识,否则用“o”标识(o -> overlap)。图1中各子类实体概念上是排他的。
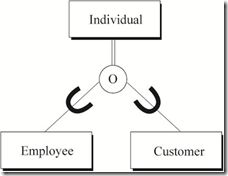
对员工、客户实体进行泛化,抽象出超类实体个人,得到如下关系图。由于部分Employee也可能是Customer,故子类实体Employee与Customer之间概念是重叠的。
图2 Individual与Employee、Customer之间的泛化关系
完备性约束表示所有子类型在当前系统中是否能完全覆盖超类型。若能完全覆盖则在超类型与圆圈之间用双线标识(可以把双线理解为等号)。在图2中子类实体Employee与Customer能完全覆盖超类Individual实体。
聚合(Aggregation)
聚合是与泛化抽象不同的另一种超类型与子类型间的抽象。
泛化表示“is-a”语义,聚合表示“part-of”语义。聚合中子类型与超类型间没有继承关系。
聚合关系的标记法是在圆圈中标识字母“A”来表示。
下图表示软件产品由程序与用户手册组成。
图3 Software-product与Program、User’s Guide之间的聚合关系
三元关系(Ternary Relationships)
当通过二元关系无法准确描述三个实体间的联系时,我们需要使用三元关系。
三元关系中“连通数”的确定方法:
- 以三元关系中的一个实体作为中心,假设另两个实体都只有一个实例
- 若中心实体只有一个实例能与另两个实体的一个实例进行关联,则中心实体的连通数为“一”
- 若中心实体有多于一个实例能与另两个实体实例进行关联,则中心实体的连通数为“多”
注:什么时候需要使用三元关系的实例请参看:《一步一步设计你的数据库三》中的“关系的度(Degree of a Relationship)”小节。关系的“连通数”概念请参看:《一步一步设计你的数据库三》的“关系的连通数(Connectivity of a Relationship)”小节。
我们来看几个三元关系的实例,注意各个图中关系的度,并理解其中的语义。
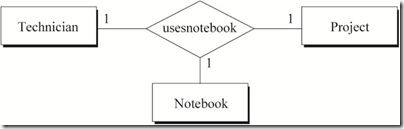
图4 技术员在项目中使用手册的关系
图4中蕴含的语义为:
- 一名技术员对于每一个项目使用一本手册
- 每一本手册对于每一个项目属于一名技术员
- 一名技术员可能在做多个项目,对于不同的项目维护不同的手册
用数学中的函数依赖表示图4的关系:
- emp-id, project-name -> notebook-no
- emp-id, notebook-no -> project-name
- project-name, notebook-no -> emp-id
图5 员工被分配不同地点的项目之间的关系
图5中蕴含的语义为:
- 每一个员工在一个地点只能被分配一个项目,但可以在不同地点做不同的项目
- 在一个特定的地点,一个员工只能做一个项目
- 在一个特定的地点,一个项目可以由多个员工来做
用数学中的函数依赖表示图5的关系:
- emp-id, loc-name -> project-name
- emp-id, project-name -> loc-name
图6 经理管理项目与工程师的关系
图6中蕴含的语义为:
- 一名经理手下的一名工程师可能参与多个项目
- 一名经理管理的一个项目可能会有多名工程师
- 做某一个项目的一名工程师只会有一名经理
用数学中的函数依赖表示图6的关系:
- project-name, emp-id -> mgr-id
图7 员工在项目中使用技能的关系
图7中蕴含的语义为:
- 一名员工在一个项目中可以使用多种技能
- 一名员工的一种技能可以在多个项目中使用
- 一种技能在一个项目中可以被多名员工使用
图7各实体之间没有函数依赖
上述4种形式的三元关系,连通数为“一”的实体数量与该三元关系反映的函数依赖语义的数目一致。
三元关系也能有属性。属性值由三个实体的键的组合唯一确定。
n元关系(General n-ary Relationships)
三元关系可以扩展到n元关系,描述n个实体之间的关系。
一般而言,n元关系中每一个连通数为“一”的实体的键都会出现在一个函数依赖表达式的右侧。
对于n元关系,使用语言来表达其中的约束相对较为困难。建议使用数学形式即函数依赖(FD)来表现。
n元关系的函数依赖条目数量与关系图中“一”端实体的数量相同(0~n条)。
n元关系的函数依赖表达式包含n个元素,n-1个元素出现在表达式左侧,1个元素出现在右侧。
图8 n元关系图例
排他性约束(Exclusion Constraint)
一般(默认)情况下,多种关系之间是兼容的“或”关系,即允许任意或所有实体参与这些关系。
在某些情况下,多种关系之间是非兼容性“或”关系,即参与关系的实体只能选择其中一种关系,不能同时选择多种关系。
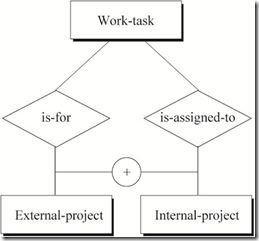
下图表示的语义为:一项工作任务要么被归为外部项目中,要么被归为内部项目中,不可能同时属于外部项目和内部项目。
图9 排他性约束关系图例