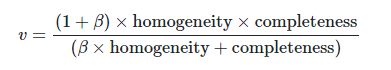聚类：KMeans、DBSCAN、层次聚类AgglomerativeClustering及聚类评价指标

聚类（无监督学习）

目标

簇内相似度高，簇间相似度低

聚类性能度量

1. 外部指标：将聚类结果与某个“参考模型”进行比较。
2. 内部指标：直接考察聚类结果，不利用任何参考模型。

聚类方法

一、KMeans

给定k个聚类的数量固定，将观察值分配给这些聚类，以使各个聚类（对于所有变量）的均值尽可能彼此不同。

KMeans（n_clusters = 8，*，init ='k-means ++'，n_init = 10，max_iter = 300，tol = 0.0001，precompute_distances ='deprecated'，verbose = 0，random_state = None，copy_x = True，n_jobs ='deprecated '，algorithm ='auto' ）

参数解释

n_clusters——聚类的个数

二、层次聚类

AgglomerativeClustering(n_clusters=2, *, affinity='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward', distance_threshold=None)

参数解释

n_clusters——聚类的个数
linkage——连接方法。ward（方差最小化）complete（两组中所有观测值间的最大距离）average（平均距离）single（最小距离）
affinity——用于计算linkage的度量。“euclidean”:欧几里得距离(如果linkage 是 “ward”, 则affinity只可选为此选项) ，“l1”，“l2”

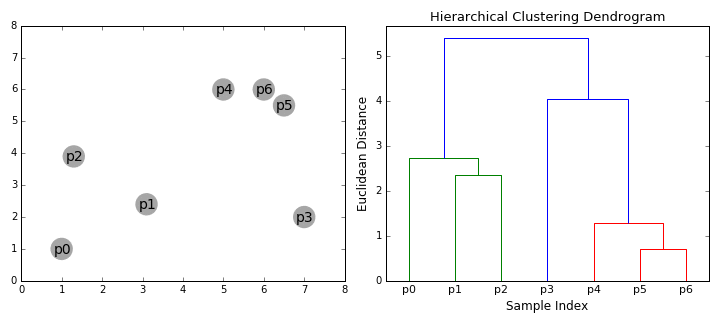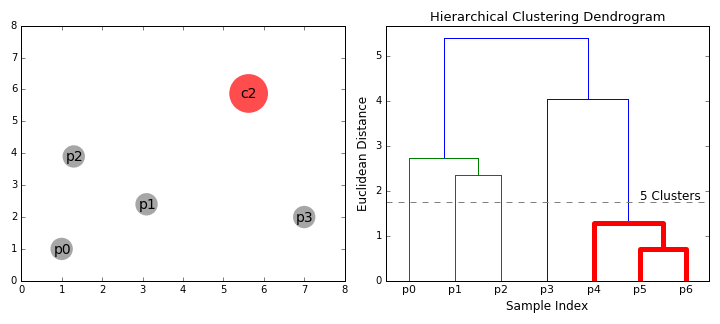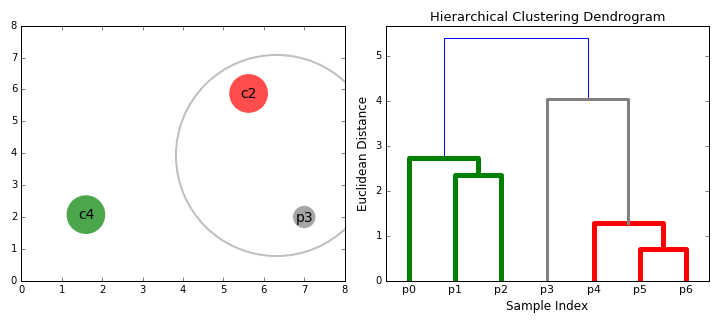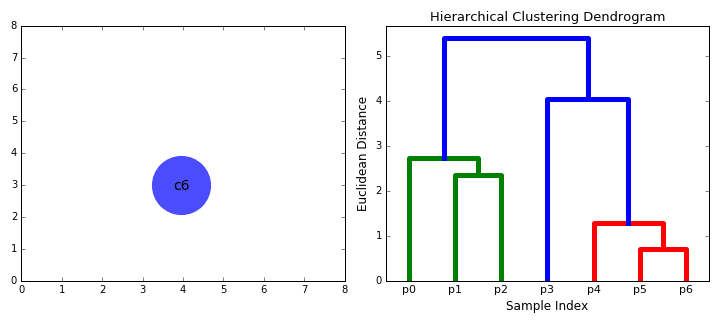
1）先计算样本之间的距离。每次将距离最近的点合并到同一个类。然后，再计算类与类之间的距离，将距离最近的类合并为一个大类。不停的合并，直到合成了一个类。其中类与类的距离的计算方法有：最短距离法，最长距离法，中间距离法，类平均法等。比如最短距离法，将类与类的距离定义为类与类之间样本的最短距离。

2）层次聚类算法根据层次分解的顺序分为：自下底向上和自上向下，即凝聚的层次聚类算法和分裂的层次聚类算法（agglomerative和divisive），也可以理解为自下而上法（bottom-up）和自上而下法（top-down）。自下而上法就是一开始每个个体（object）都是一个类，然后根据linkage寻找同类，最后形成一个“类”。自上而下法就是反过来，一开始所有个体都属于一个“类”，然后根据linkage排除异己，最后每个个体都成为一个“类”。这两种路方法没有孰优孰劣之分，只是在实际应用的时候要根据数据特点以及你想要的“类”的个数，来考虑是自上而下更快还是自下而上更快。至于根据Linkage判断“类”的方法就是最短距离法、最长距离法、中间距离法、类平均法等等（其中类平均法往往被认为是最常用也最好用的方法，一方面因为其良好的单调性，另一方面因为其空间扩张/浓缩的程度适中）。为弥补分解与合并的不足，层次合并经常要与其它聚类方法相结合，如循环定位。
AGNES是一种采用自底向上聚合策略的层次聚类算法。AGNES算法也被称为“单链接”（single）、“全链接”（complete）、“均链接”（average）算法。

三、DBSCAN

根据半径eps和半径内的最小样本数min_samples，以半径内的每一个样本为原点，不停“生长”，当该样本半径内的最小样本数小于min_samples时，停止“生长”。

DBSCAN(eps=0.5, *, min_samples=5, metric='euclidean', metric_params=None, algorithm='auto', leaf_size=30, p=None, n_jobs=None)~

参数解释

eps——半径
min_samples——半径内的最小样本数

聚类评价指标（有真实标签）

调整后的rand指数——adjusted Rand index

有界范围[-1，1]：负值为分类效果不好（独立标签），相似的聚类具有正的ARI，1.0是完美匹配分数；对于均匀分布的数据，ARI接近于0。

 from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
metrics.adjusted_rand_score(labels_true, labels_pred)
0.24...

adjusted_rand_score是对称的：交换参数不会更改分数
在预测的标签中置换0和1，将2重命名为3，可以获得相同的分数：

labels_pred = [1, 1, 0, 0, 3, 3]
metrics.adjusted_rand_score(labels_true, labels_pred)
0.24...~

调整后的互信息（AMI）——Adjusted Mutual Information

互信息用来衡量两个分布一致性，并且忽略顺序。直观上，互信息度量 X 和 Y 共享的信息：它度量知道这两个变量其中一个，对另一个不确定度减少的程度。例如，如果 X 和 Y 相互独立，则知道 X 不对 Y 提供任何信息，反之亦然，所以它们的互信息为零。
随机的预测AMI会接近于0；最大上界为1，说明预测完全正确。

from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
metrics.adjusted_mutual_info_score(labels_true, labels_pred)  
0.22504...~

规范化互信息（NMI）——Normalized Mutual Information
mutual_info_score，adjusted_mutual_info_score和 normalized_mutual_info_score是对称的：交换参数不改变分数

homogeneity_score、completeness_score

同质性 homogeneity：每个聚类仅包含单个类的成员。
完整性 completeness：给定类的所有成员都分配给同一集群。
V-度量是以上两者的调和平均数。
评分范围：0—1（越高越好）

 from sklearn import metrics
 labels_true = [0, 0, 0, 1, 1, 1]
 labels_pred = [0, 0, 1, 1, 2, 2]
 metrics.homogeneity_score(labels_true, labels_pred)
0.66...
 metrics.completeness_score(labels_true, labels_pred)
0.42...~

它们的谐波均值称为V-measure由v_measure_score以下公式计算

metrics.v_measure_score(labels_true, labels_pred)
0.51...~

beta 默认值为1.0，但对于beta使用小于1的值：

metrics.v_measure_score(labels_true, labels_pred, beta=0.6)
0.54...~

重量更大将归因于同质性，并且使用大于1的值：

metrics.v_measure_score(labels_true, labels_pred, beta=1.8)
0.48...~

可以用同质性和完整性 来定性分析具有不良V度量的聚类， 以更好地感觉到分配所造成的“错误”类型。
V度量实际上等效于上面讨论的互信息（NMI），聚合函数是算术平均值。
齐次性，完整性和V度量可使用homogeneity_completeness_v_measure计算

metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(0.66..., 0.42..., 0.51...)~

优点：0代表差，1代表好；不需要对簇结构进行假设，可以对不同聚类算法进行比较。

缺点：当簇数目比较大时，这三者的值都不会趋近于0；当样本数多于1000或者簇数目少于10时可以避免这个问题，其他情况可以选择适用ARI；另外这三个指标需要知道样本的真实分类。

Fowlkes-Mallows scores

Fowlkes-Mallows分数FMI定义为成对精度和召回率的几何平均值：

其中TP，“正阳性”的数量（即在真标签和预测标签中属于同一聚类的点对的数量）
FP是“ 假阳性”的数目（即属于“ 正标签”和“预测标签” 的点对的数量）在真正的标签，而不是在所预测的标签相同的簇）
和FN是的数量假阴性（即是，在所预测的标签和未在真标记）相同的簇所属的一对点的数目。
分数范围是0到1。较高的值表示两个聚类之间的相似性良好。

优点：随机预测值趋近于0；上限为1，表示预测完全正确；不需要对簇类型进行假设。

缺点：需要知道样本类别。

聚类评价指标（无真实标签）

轮廓系数—Silhouette Coefficient

每个样本都有各自的轮廓系数，该系数由两个分数组成：
a：样本与同一类别中所有其他点之间的平均距离。
b：样本与下一个最近的簇中所有其他点之间的平均距离。
单个样本的Silhouette系数s为：

注意：仅当标签数为2 <= n_labels <= n_samples-1时，才定义轮廓系数。

即聚类的类别大于1，且小于样本数。

此函数返回所有样本的平均轮廓系数。

最佳值为1，最差值为-1。接近0的值表示重叠的群集。负值通常表示样本已分配给错误的聚类，因为不同的聚类更为相​​似。

from sklearn import metrics
from sklearn.cluster import KMeans
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
metrics.silhouette_score(X, labels, metric='euclidean')
0.55...

优点：不需要知道样本标签；-1表示存在错误聚类，0表示有交叉的簇，1表示高密度聚类。

缺点：凸形簇的轮廓系数通常高于其他类型的簇。

Calinski-Harabasz Index

该指数是所有集群的集群间离散度和集群间离散度之和的比率（其中，离散度定义为距离平方的总和），也称为方差比标准。

Calinski-Harabaz的分数S被定义为组间离散与组内离散的比率，该分值越大说明聚类效果越好。

B_K​是组间离散矩阵
W_K是组内离散矩阵

n是样本点数，c_q 是在聚类q中的样本点，C_q 是聚类q的中心点，n_q 是聚类q中的样本点数量，c是E的中心。

计算Calinski和Harabasz得分。也称为差异比率标准。得分定义为簇内分散体和簇间分散体之间的比率。

from sklearn import metrics
from sklearn.cluster import KMeans
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
metrics.calinski_harabasz_score(X, labels)
561.62...

优点：易计算（比轮廓系数快很多）；当类聚合地很好，类间差距很大时，该值增大，反映了簇的标准概念。

缺点：对于凸形簇，该值会很大，但是对于其他类型簇，如基于密度型，该值无可奈何。

Davies-Bouldin Index

分数定义为每个群集与其最相似群集的平均相似性度量，其中相似度是群集内距离与群集间距离的比率。因此，距离更远且分散程度较低的群集将获得更好的分数。

最低分数为零，值越低表示聚类越好。

from sklearn.cluster import KMeans
from sklearn.metrics import davies_bouldin_score
kmeans = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans.labels_
davies_bouldin_score(X, labels)
0.6619...

缺点：对于凸性簇，该值会高一点；质心距离限制距离度量欧氏空间；良好的值并不意味着最好的分类结果。

Contingency Matrix—权变矩阵

报告每个真实/预测的聚类对的相交基数。权变矩阵为所有聚类指标提供了足够的统计数据，在这些度量中样本是独立且分布均匀的，不需要考虑某些未聚类的实例。

from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
       [0, 1, 2]])

输出数组的第一行指示存在三个样本，其真实簇为“ a”。其中两个在预测聚类0中，一个在1中，一个都不在2中。第二行表示存在三个样本，其真实聚类为“ b”。其中，没有一个在预测聚类0中，一个在1中，两个在2中。

缺点：1.列联矩阵对于少数群集很容易解释，但对于大量群集则很难解释。
2.它没有给出一个单一的指标来用作集群优化的目标。