统计基础之概率论与数理统计(完结)

1、随机变量及其分布：
1.1、离散型随机变量（0-1分布、二项分布、泊松分布、几何分布）
1.1.1、0-1分布
0—1分布就是n=1情况下的二项分布。

1.1.2、二项分布（伯努利分布）
二项分布就是重复n次独立的伯努利试验。
如果存在X~B(n, p)这样一个二项分布，也就是说X是呈现出二项分布的随机变量，n表示试验的总数，p表示每个试验中得到成功结果的概率，那么X的期望值E(X)=np，方差Var(X)=np(1-p)。
多项分布是二项式分布的推广。

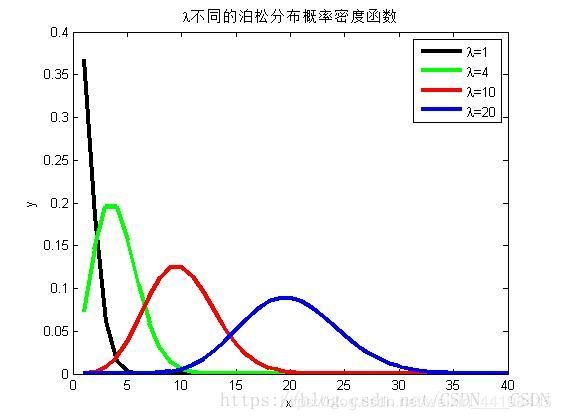
1.1.3、泊松分布
泊松分布公式

泊松分布的期望为E(X)=λ，方差D(X)=λ
1.1.4 、几何分布
几何分布是帕斯卡分布当r=1时的特例。
1.2、连续型随机变量及其分布（均匀分布、指数分布、正态分布（标准正态分布）、负指数分布、伽马分布）

1.2.1、均匀分布
假设x服从[a,b]上的均匀分布，则x的概率密度函数如下

概率密度图像
1.2.2、指数分布
指数分布的概率密度函数

指数分布的区间是[0,∞)。 如果一个随机变量X呈指数分布，则可以写作：X~ E（λ）
x是给定的时间；λ为单位时间事件发生的次数；e＝2.71828。
指数分布概率密度曲线如下图：

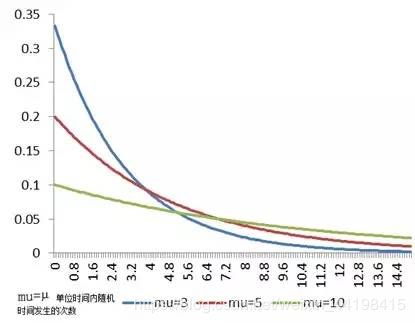
指数分布具有以下特征：
（1）随机变量X的取值范围是从0到无穷；
（2）极大值在x＝0处，即f(x)＝λ；
（3）函数为右偏，且随着x的增大，曲线稳步递减；
（4）随机变量的期望值和方差为µ＝1/λ，σ2＝1/λ2。
通过对概率密度函数的积分，就可以得到相应的概率，其表达式有两种
P(X≥x)＝e-λx
P(X≤x)＝1－e-λx

1.2.3、正态分布，又名高斯分布。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布N(0,1)。
其概率密度函数为(标准正态分布，μ=0，σ=1)

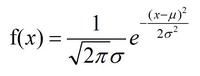
图形特征
集中性：正态曲线的高峰位于正中央，即均数所在的位置。
对称性：正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交。
均匀变动性：正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。
曲线与横轴间的面积总等于1，相当于概率密度函数的函数从正无穷到负无穷积分的概率为1，即图形面积为1。频率的总和为100%。
正态分布的概率密度曲线呈钟形，因此又被称为钟形曲线。如图所示：

μ是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小。正态分布以X=μ为对称轴，左右完全对称。正态分布的期望、均数、中位数、众数相同，均等于μ。
σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。
由于“小概率事件”和假设检验的基本思想 “小概率事件”通常指发生的概率小于5%的事件，认为在一次试验中该事件是几乎不可能发生的。由此可见X落在(μ-3σ,μ+3σ)以外的概率小于千分之三，在实际问题中常认为相应的事件是不会发生的，基本上可以把区间(μ-3σ,μ+3σ)看作是随机变量X实际可能的取值区间，这称之为正态分布的“3σ”原则。
以上都是常用的，还有其他大神总结的比较完整，网址https://blog.csdn.net/qq_38984677/article/details/81110450

2、多维随机变量及其分布
2.1、联合分布
2.2、边缘分布
2.3、条件分布
https://blog.csdn.net/thither_shore/article/details/52192553

3、随机变量的数字特征
3.1、数据的频数分析：利用频数分析和交叉频数分析来检验异常值。
通过频数分析可以了解数据文件中单个变量的分布情况，但如果要了解多个变量的分布情况则需要使用交叉分组下的频数分析。（spss交叉分组下的频数分析—案例1）
3.2、数据的集中趋势分析：数据的集中趋势分析是用来反映数据的一般水平，常用的指标有平均值、中位数和众数等。
3.2.1、平均值（Mean）：是衡量数据的中心位置的重要指标，反映了一些数据必然性的特点，包括算术平均值、加权算术平均值、调和平均值和几何平均值。
3.2.1.1、算数平均值：

3.2.1.2、几何平均值：

值得注意的是，几何平均值是相对于正数而言的，也就是说上面的X1,X2,…Xn必须是正数。
3.2.1.3、均方根平均值：

3.2.1.4、调和平均值计算方法为　N/(1/x1+1/x2+…+1/xn)
3.2.1.5、加权平均值算法为

3.2.2、中位数（Median）：是另外一种反映数据的中心位置的指标，其确定方法是将所有数据以由小到大的顺序排列，位于中央的数据值就是中位数。
1.2.3众数（Mode）：是指在数据中发生频率最高的数据值。
综上，如果各个数据之间的差异程度较小，用平均值就有较好的代表性；而如果数据之间的差异程度较大，特别是有个别的极端值的情况，用中位数或众数有较好的代表性。

3.3、数据的离散程度分析：数据的离散程度分析主要是用来反映数据之间的差异程度，常用的指标有全距、四分差、平均差、方差、标准差。
3.3.1、全距，也称极差(range)，最大值与最小值之间的差距。
3.3.2、四分差，又称四分位距，IQR = Q3 − Q1，第三四分位数和第一四分位数的差距（常用于分析箱线图）。
3.3.3、均值

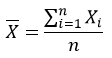
3.3.4、平均差（Mean Deviation）是表示各个变量值之间差异程度的数值之一。指各个变量值同平均数的离差绝对值的算术平均数。
平均差异大，表明各标志值与算术平均数的差异程度越大，该算术平均数的代表性就越小；平均差越小，表明各标志值与算术平均数的差异程度越小，该算术平均数的代表性就越大。因离差和为零，离差的平均数不能将离差和除以离差的个数求得，而必须将离差取绝对数来消除正负号。平均差是反应各标志值与算术平均数之间的平均差异。
3.3.5、方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。

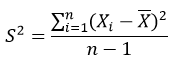
3.3.6、标准差（Standard Deviation），标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。

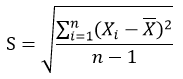
3.3.7、由方差延伸——协方差
协方差就是这样一种用来度量两个随机变量关系的统计量。我们可以仿照方差的定义：

来度量各个维度偏离其均值的程度，协方差可以这样来定义：

3.3.8、相关系数：是研究变量之间线性相关程度的量，一般用字母 r 表示。由于研究对象的不同，相关系数有多种定义方式，较为常用的是皮尔逊相关系数。
4、大数定律及中心极限定理
4.1、大数定律
在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。
通俗地说，如果统计数据足够大，那么事物出现的频率就能无限接近它的期望值。
大数定律有若干个表现形式。如：切比雪夫大数定理、伯努利大数定律、辛钦大数定律。

4.2、中心极限定理
中心极限定理是说：样本的平均值约等于总体的平均值(在没有办法得到总体全部数据的情况下，我们可以用样本来估计总体)。
不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布。

5、描述统计
5.1、数据分布通常的描述指标：偏度衡量的是样本分布的偏斜方向和程度；而峰度衡量的是样本分布曲线的尖峰程度。
a.偏度衡量随机变量概率分布的不对称性，是相对于均值不对称程度的度量。
若偏度为负，则均值左侧的离散度比右侧强;若偏度为正，则均值左侧的离散度比右侧弱。对于正态分布(或严格对称分布)偏度等于 0。即：偏度为负（负偏）/正（正偏）表示在概率密度函数左侧/右侧的尾部比右侧的长，长尾在左侧/右侧。偏度为零表示数值相对均匀地分布在平均值的两侧，但不一定意味着一定是对称分布。
b.峰度是概率密度分布曲线在平均值处峰值高低的特征数。
直观看来，峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量，如果峰度大于三，峰的形状比较尖，比正态分布峰要陡峭。反之亦然。

5.2、直方图
直方图适用于连续性数据。
将一个变量的不同等级的相对频数用矩形块标绘的图表(每一矩形的面积对应于频数)。
直方图(Histogram)又称柱状图、质量分布图。是一种统计报告图，由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类型，纵轴表示分布情况。

5.3、箱线图：用R语言实现箱线图——案例2、用Excel实现箱线图——案例3、用Python实现箱线图——案例4
箱线图：主要由最大值、最小值、上四分位（Q3）、中位数（Q2）、下四分位（Q1）、异常值构成。我们一般认为合理数据在区间（Q1-1.5△Q,Q3+1.5△Q）内，其中△Q=Q3-Q1，超出此范围则为异常值（同时也可结合实际情况进行判断）。此外，箱线图还可粗略估计数据偏态分布，当中位数偏向上四分位时，数据呈右偏态；当中位数偏向下四分位时，数据呈左偏态。

5.4、经验分布图：用Excel实现经验分布图——案例5、用R语言实现经验分布图——案例6
经验分布函数是将数据按照从小到大的顺序排列后，统计其出现的累计概率发布的一种简单算法。经验分布函数对离散型和连续性随机变量都适用。

6、抽样分布（因为很多时候不可能用到全部样本，所以要抽样，进行分析）
6.1、卡方分布
6.2、t分布
6.3、F分布
常见的三大抽样分布：卡方分布、t分布、F分布，都是基于正态分布导出的，用来检验正态总体。（正态分布是与自由度无关的一条曲线； t分布是依自由度而变的一组曲线。）
正态分布是统计学中一种很重要的理论分布，是许多统计方法的理论基础。正态分布有两个参数，μ和σ，决定了正态分布的本质。为了应用和计算方便，常将一般的正态变量X通过u变换[(X-μ)/σ]转化成标准正态变量u，以使原来各种形态的正态分布都转换为μ=0，σ=1的标准正态分布,亦称u分布。对于标准正态分布来说，μ是数据整体的平均值，σ是整体的标准差。但实际操作过程中，人们往往难以获得μ和σ。因此人们只能通过样本对这两个参数做出估计，用样本平均值和样本标准差代替整体的平均值和标准差，从而得出了t分布。
另外从图像的层面说，正态分布的位置和形态只与μ和σ有关，而t分布不只与样本平均值和样本标准差有关，还与自由度相关。
https://blog.csdn.net/anshuai_aw1/article/details/82735201

7、参数估计
7.1、点估计
7.1.1、矩估计法
7.1.2、最大似然估计法

7.2、估计量的评选标准
7.2.1、无偏性
7.2.2、有效性
7.2.3、相合性

7.3、区间估计
置信区间的求法。刷题。
https://blog.csdn.net/ymf827311945/article/details/78069980

8、假设检验（8.1-8.6都是临界值法）
假设检验：是数理统计学中根据一定假设条件由样本推断总体的一种方法。具体作法是：根据问题的需要对所研究的总体作某种假设，记作H0；选取合适的统计量，这个统计量的选取要使得在假设H0成立时，其分布为已知；由实测的样本，计算出统计量的值，并根据预先给定的显著性水平进行检验，作出拒绝或接受假设H0的判断。
常用的假设检验方法有u—检验法、t检验法、χ2检验法(卡方检验)、F—检验法，秩和检验等。
原理：https://wenku.baidu.com/view/fefcac6b1eb91a37f1115cc0.html
8.1、显著性检验
8.2、Z检验
8.3、t检验
https://blog.csdn.net/ch1209498273/article/details/78313883
8.4、卡方检验
https://blog.csdn.net/ludan_xia/article/details/81737669
8.5、F检验
F检验（F-test），最常用的别名叫做联合假设检验（英语：joint hypotheses test），此外也称方差比率检验、方差齐性检验。

对F检验只是简单理解。

F检验又叫方差齐性检验。在两样本t检验中要用到F检验。从两研究总体中随机抽取样本，要对这两个样本进行比较的时候，首先要判断两总体方差是否相同，即方差齐性。若两总体方差相等，则直接用t检验，若不等，可采用t’检验或变量变换或秩和检验等方法。其中要判断两总体方差是否相等，就可以用F检验。F检验法是英国统计学家Fisher提出的，主要通过比较两组数据的方差S^2，以确定他们的精密度是否有显著性差异。至于两组数据之间是否存在系统误差，则在进行F检验并确定它们的精密度没有显著性差异之后，再进行t检验。

此处本人理解，T检验之前要进行F检验，指的是对两样本均数(mean)差别的显著性进行检验时，才会要进行F检验，来判断方差是否齐性。其它情况不用判断F检验，比如单样本检验和配对检验等情况不用，或样本是在同一总体中的两次抽样，也不用进行F检验

9、方差分析
一、方差分析的基本思想

1. 方差分析的概念
   方差分析（ANOVA）又称变异数分析或F检验，其目的是推断两组或多组资料的总体均数是否相同，检验两个或多个样本均数的差异是否有统计学意义。我们要学习的主要内容包括单因素方差分析即完全随机设计或成组设计的方差分析和两因素方差分析即配伍组设计的方差分析。
2. 方差分析的基本思想
   下面我们用一个简单的例子来说明方差分析的基本思想：
   如某克山病区测得11例克山病患者和13名健康人的血磷值（mmol/L）如下，
   患者：0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11
   健康人：0.54 0.64 0.64 0.75 0.76 0.81 1.16 1.20 1.34 1.35 1.48 1.56 1.87
   问该地克山病患者与健康人的血磷值是否不同？
   从以上资料可以看出，24个患者与健康人的血磷值各不相同，如果用离均差平方和（SS）描述其围绕总均数的变异情况，则总变异有以下两个来源：
   （1）组内变异，即由于随机误差的原因使得各组内部的血磷值各不相等；
   （2）组间变异，即由于克山病的影响使得患者与健康人组的血磷值均数大小不等。
   而且：SS总=SS组间+SS组内 v总（自由度）=v组间+v组内

如果用均方（即自由度v去除离均差平方和的商）代替离均差平方和以消除各组样本数不同的影响，则方差分析就是用组内均方去除组间均方的商（即F值）与1相比较，若F值接近1，则说明各组均数间的差异没有统计学意义，若F值远大于1，则说明各组均数间的差异有统计学意义。实际应用中检验假设成立条件下F值大于特定值的概率可通过查阅F界值表（方差分析用）获得。
3. 方差分析的应用条件
应用方差分析对资料进行统计推断之前应注意其使用条件，包括：
（1）可比性，若资料中各组均数本身不具可比性则不适用方差分析。
（2）正态性，即偏态分布资料不适用方差分析。对偏态分布的资料应考虑用对数变换、平方根变换、倒数变换、平方根反正弦变换等变量变换方法变为正态或接近正态后再进行方差分析。
（3）方差齐性，即若组间方差不齐则不适用方差分析。多个方差的齐性检验可用Bartlett法，它用卡方值作为检验统计量，结果判断需查阅卡方界值表。
二、方差分析的主要内容
根据资料设计类型的不同，有以下两种方差分析的方法：

1. 对成组设计的多个样本均数比较，应采用完全随机设计的方差分析，即单因素方差分析。

2. 对随机区组设计的多个样本均数比较，应采用配伍组设计的方差分析，即两因素方差分析。
   两类方差分析的基本步骤相同，只是变异的分解方式不同，对成组设计的资料，总变异分解为组内变异和组间变异（随机误差），即：SS总=SS组间+SS组内，而对配伍组设计的资料，总变异除了分解为处理组变异和随机误差外还包括配伍组变异，即：SS总=SS处理+SS配伍+SS误差。整个方差分析的基本步骤如下：
   （1） 建立检验假设；
   H0：多个样本总体均数相等。
   H1：多个样本总体均数不相等或不全等。检验水准为0.05。
   （2） 计算检验统计量F值；
   （3）确定P值并作出推断结果。
   三、多个样本均数的两两比较
   经过方差分析若拒绝了检验假设，只能说明多个样本总体均数不相等或不全相等。若要得到各组均数间更详细的信息，应在方差分析的基础上进行多个样本均数的两两比较。

   多个样本均数间两两比较
   多个样本均数间两两比较常用q检验的方法，即 Newman-kueuls法，其基本步骤为：
   建立检验假设–>样本均数排序–>计算q值–>查q界值表判断结果。
   多个实验组与一个对照组均数间两两比较
   多个实验组与一个对照组均数间两两比较，若目的是减小第II类错误，最好选用最小显著差法（LSD法）；若目的是减小第I类错误，最好选用新复极差法，前者查t界值表，后者查q界值表。