2016-10-26陈伟才人工智能学堂
前面几篇都是轻松愉快的文章,这篇就来点烧脑的,调节调节。本文主要讲解卷积神经网络CNN,这也是TensorFlow MNIST官方进阶篇采用的深度学习算法。深度学习是机器学习的一个重要分支,特别是这几年超级互联网公司如Google以及大数据的推动下,取得新的进展和突破。
一、神经网络
神经网络Neural Networks方面的研究其实在二十世纪四十年代就开始了,尤其以N-P神经元模型为代表,掀起了神经网络发展的第一个高潮期。当时单层的神经网络无法解决非线性问题域,导致当时的神经网络适应场景受限,对神经网络的研究随之就跌入谷底。
直到二十世纪八十年代,BP算法的轰动,解决了多层神经网络训练的算法问题,从而推动神经网络解决了非线性问题领域,推动神经网络第二次高潮。
随着进入二十一世纪,互联网技术,分布式系统,特别是这几年云计算、大数据在互联网公司如Google,Facebook的推动下,神经网络分支下的“深度学习Deep Learning”再次将神经网络推向高潮。
轰动全球的2016年3月AlphaGo一款围棋人工智能程序,由谷歌(Google)旗下DeepMind公研制。这个程序在2016年3月与围棋世界冠军、职业九段选手李世石进行人机大战,并以4:1的总比分获胜。该程序的原理就是深度学习,引领着大家对神经网络学习的第三次浪潮。本公众号“人工智能学堂”也是在这次浪潮的推动下产生的。
M-P神经元模型
神经网络,大家很容易想到高中生物课本上的神经元细胞组织,每个神经元只有一个轴突,可以把化学物质传送到另一个神经元,收到神经元同样会做出相应的反应,把信息传递到下一个神经元,如此循环。
神经网络就是受到生物学神经系统的启发,来模拟生物神经系统对外界真实环境做出的交付式反应。这里需要澄清的是,神经网络的目的不是仅仅为了生物神经系统,而是为了实现一套网络,能够学习,并且能够做出相应的反应。
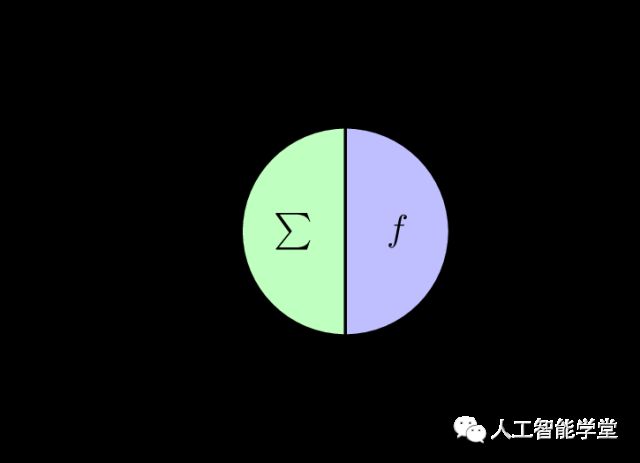
神经网络中最基本的要素是神经元模型,目前最经典的模型是M-P神经元模型,是1943年由McCulloch and Pitts提出的。如下图所示:
如上图所示,神经元模型中,神经元接受来自 n 个其他神经元(xi)传递过来的信号,这些信号是带有权限Weight(Wij),对这些神经元传递的信息进行求和,并与该神经元的阈值进行比对,然后才通过激活函数f的处理,给出最终的输出,该输出即该神经元对此次输入的信号做出的反应。如下公式表示上述过程:
对于激活函数,其效果就是Yes和No的判断,也就是用一个阶跃函数即可。但是阶跃函数的不连续缺陷,目前界内用的比较多的是Sigmoid函数。
Sigmoid函数取值范围是[0, 1],正无穷大则收敛于1,负无穷大则收敛于0,切在整个区间是连续的,光滑的,如下图所示:
二、传统神经网络
把许多个神经元连接起来,上一个输入,经过本神经元处理后的信息,作为下一个神经元的输入,如此下去,便组成了神经网络。我们先看两个输入神经元的场景。
套入上一节的公式得:
y = f(X1 * W1 + X2 * W2 -θ)
上述模型,很容易实现与、或、非:
与:即 X1 = X2 = 1时,y = 1,显然只需令 W1 = W2 = 1,θ = 2;
或:即 X1 = 1 或者 X2 = 1,时,y = 1,显然只需令 W1 = W2 = 1,θ = 0.5;
非:即 X1 = 1 时,y = 0,或者X1 = 0 时,y = 1,显然只需令 W = -0.6, W2 = 0,θ = 0.5;
单层的神经系统,其学习能力是有限的,对于很多问题,如非线性问题,单层神经系统是无法解决的。
多层前馈神经网络
要解决非线性可分问题,需要考虑使用多层功能的神经系统。多层升级系统具有如下特征:
每一层的神经元与下一层神经元全连接
同一层神经元之间不存在同层连接
不存在跨层神经元连接
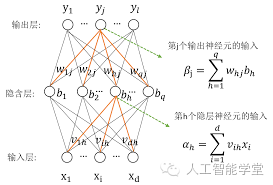
具备上述3个特征的神经系统,一般称为多层前馈神经网络,multi-layer feedforward neural networks,如下图所示:
上图中,输入层神经元接收外界的输入,隐含层与输出层神经元对信号进行处理加工,最终的结果是通过输出层对外输出的。即输入层神经元只负责信息的接收,而隐含层和输出层神经元是需要对信息进行加工处理的。
三、卷积神经网络
上节中多层前馈神经网络扩展性不好,原因主要有两点,一是神经元是全连接的,二是同层的神经元是相互独立的。这样导致随着隐含层层数或者隐含层的神经元个数的增加,需要建立的链接是指数级的增长,其计算量是极大的挑战,或者用机器学习领域的专有词汇描述是overfitting,即过度拟合。
以CIFAR-10为例,一张图片的大小是 32*32*3 (32 width,32 height, 3 colors),如果是单层全连接神经网络,则需要32*32*3 = 3072个weights,如果图片大小是200*200*3(200 width,200 height, 3 colors),则需要200*200*3 = 120000个weights。
多层前馈神经网络需要进行改良,提升其扩展性才能满足实际用于的需求。为此,卷积神经网络CNN(Connetional Neural Networks)应用而生。那么CNN是如何做到降低参数的了?
局部连通性
第一个是Local Connectivity,局部连通性。与全连接神经网络不同的是,CNN的神经元和下一层神经元不是全连接的。我们可以这么来理解,对于一张图片,图片本身也是分不同部分组成的,而每个部分,他们可以拥有类似的权值参数。
比方说一张人头的照片,有头发,鼻子,耳朵,嘴巴,牙齿,眼睛等等。所以我们在进行学习的时候,没必要多整个人头进行全量学习,而是先对不通的部位进行学习,最后再汇总全面学习。这样无疑降低了神经网络权值参数的学习成本。
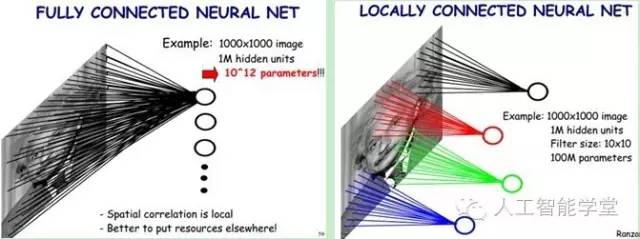
上图假如是1000*1000的图片,左边是全连接神经网络,对于1M的神经元来说,它必须学习所有的input信息,就意味着它必须学习1000*1000*1M=10^12 的权值参数。右边就是CNN,如果滤波的大小10*10,10*10*1M=10^8,降低了4个数量级。
下图是 RGB CIFAR-10 image,32*32*3 (width,height,colors),作为输入层,假如CNN的滤波大小是5*5,所以对应输入层5*5*3的区域,卷积层的每个神经元需要全连接的权值参数个数为 5*5*3 = 75。注意,虽然是5*5的区域,但是必须是全深度的学习,即depth为3.途中有5个神经元,每个神经元的权值参数个数为75.
关于滤波,还有两个重要的概念,一个是stride,一个是zero-padding。stride是步幅大小,即每次滤波学习区域移动的步幅,zero-padding则是用0填充,可以想象一下,对于图片边缘的部分,学习的力度肯定没有图片中间的频繁,所以我们将图片四周都用0来填充,用0来包裹。
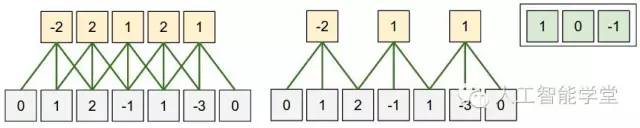
上图可以看到,input的数组为5个(1,2,-1,1,-3),两边用0填充则变为(0,1,2,-1,1,-3,0)。假设filter size为3,如果stride为1,则output有5个输出(-2,2,1,2,1),如果stride为2,则output只有3个(-2,1,1)。
参数共享
第二个是参数共享。先举一个真实的例子,2012年的ImageNet挑战赛。输入是227*227*3的图片。假设filter size F = 11,stride S = 4,没有做zero padding(实际上是做了的,原因是图片原始大小是224*224*3,只是没有特别提出来), 所以 (227 - 11)/4 + 1 = 55,且卷积层的深度K = 96,所以卷积层一共需要55 *55 * 96 = 290400个神经元,每个神经元对应出入图片227*227*3中的11*11*3的区域。即11*11*3这样一个3D区域对应一个神经元,这样一个神经元需要11*11*3 + 1 = 364个全权值参数。所以,对应227*227*3的图片输入,卷积层一共需要 364 * 290400 = 105705600 个权值参数。
227*227*3卷积层就需要105705600个weights,如果是更大的图片了,这显然也是不行的,虽然和全连接神经网络已经优化好几个数量级了。
从上面还可以观察到,11*11*3区域对应一个神经元,同时从深度方向看,depth维度的96个神经元对应同一个11*11*3区域。从depth切面看,一共有96个切片,227*227*3对应的切换一共有 55 * 55 个神经元。如果我们对同一个depth的切换的55*55个神经元采用相同的weights和bias,这样一个切换就需要11*11*3 + 1 = 364个权值参数了。对于227*227*3的图片就需要 364 * 96 = 34944. 这样权值参数的数量级又降低了4个。
这里的同一个切面的神经元采用相同的权值参数进行个数优化,在CNN中称之为参数共享,Parameters Sharing。
这里需要提点一下,为什么是同一个切面是采用参数共享,而不是深度维度采用参数共享了,笔者在第一次学习参数共享这个特性就有这个疑问。我可以简单想象一下,不同的切面就表示不同层次的卷积,每一层次的卷积作为下一个卷积的输入,所以最好按照卷积的层次也就是稳重说的切面,不同的切面采用不同的权值参数,而同一个切面的神经元采用参数共享。
CNN图解
下面以具体列子进行CNN局部连通性和参数共享进行演示。下图中是5*5*3的蓝色图片区域是原始的input,为了演示方便,将3D的图片切成3个平面纵向排列。蓝色的四周都采用0进行填充,灰色部分,可以zero padding = 2,中间 3 *3的区域是滤波器的大小,我们可以知道这个CNN卷积层是有两层的滤波器,每一层的滤波器采用相同的权值参数,所以每一层的权值参数个数为 3*3*3 + 1= 28。
我们以上图为例,卷积神经元的output是如何计算出来的。蓝色区域和红色区域对应的数字进行相乘然后再求和,最后和Bias相加,得到对应的数字,依次存放到绿色矩阵里面。第一个矩阵结果是3, 第二个矩阵的结果是2,第三个矩阵的结果是0,所以3 + 2 + 0 = 5,最后加上第一个Bias参数1,所以第一个3*3*3的区域神经输出结果是 6.
从上面的图可以看出,这个CNN卷积层需要学习到的权值参数的个数是2 * 28 = 56个,即途中红色部分。
CNN的可视化
CNN卷积过程是很复杂的,整个过程也不是很直观的,所以,对于神经网络CNN可视化,也是一个很热的领域,下图是北京大学可视化和可视分析研究小组对CNN卷积的可视化系统,系统demo地址是http://shixialiu.com/publications/cnnvis/demo/。
参考资料
Machine Learing机器学习,周志华,清华大学出版社
http://cs231n.github.io/convolutional-networks/
http://vis.pku.edu.cn/blog/%E6%9B%B4%E5%A5%BD%E7%9A%84%E7%90%86%E8%A7%A3%E5%88%86%E6%9E%90%E6%B7%B1%E5%BA%A6%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%EF%BC%88towards-better-analysis-of-deep-convolutional-neural-net/
长按二维码关注公众号人工智能学堂