语义分割算法总结（二）

承接之前的语义分割算法总结（一）

2.4 DeepLab (v1 & v2)

DeepLab v1:
通过前面的介绍，我们总结出，最后得到的分割图像质量的高低，主要取决于卷积和池化层输出数据的维度大小和数据中每一个元素的感受域大小。数据维度主要决定分割图像的分辨率等微观特征，感受域主要决定图像上各对象的分类信息等宏观特征。

最后得到的分割图像分辨率的在经过卷积和池化操作后，得到的数据的维度越大，保留的原始图像的细小特征越多，从而经过后面的反卷积或上池化恢复到原始图像大小时，得到的分割图的分辨率越高。因此有人提出了用基于稀疏卷积核的卷积层代替池化层，这样在不降低感受域大小的同时，可以提高输出数据的维度，即输出的像素点增多，从而包含更多的原始图像的细节特征，使得经过反卷积和上池化后，得到的分割图像的分辨率更高。前面也提到了，数据维度的下降，主要是由卷积层和池化层的kernel和stride大小决定的。因此DeepLab的提出者就想，如果将所有层的stride都设为1，那么输出数据的维度（即点的个数）就会更大，使得数据更加密集，包含更多的原始图像的细微特征。

因此，DeepLab将所有卷积层和池化层的stride都设为1，但是这样会出现一个问题，就是输出数据的感受域变小了，我们用下面的数据做一个例子：

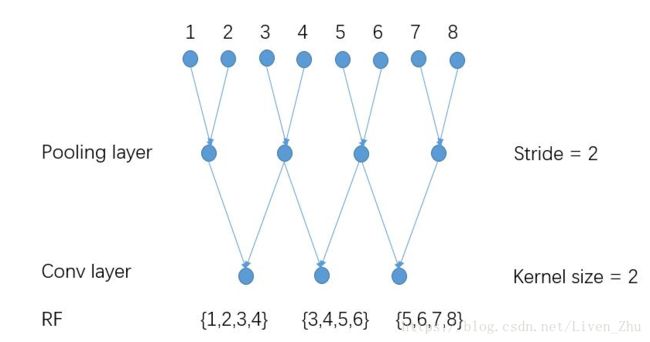
当采用如上图所示的stride和kernel大小时，输出数据的每一个元素的感受域为4个原始数据。

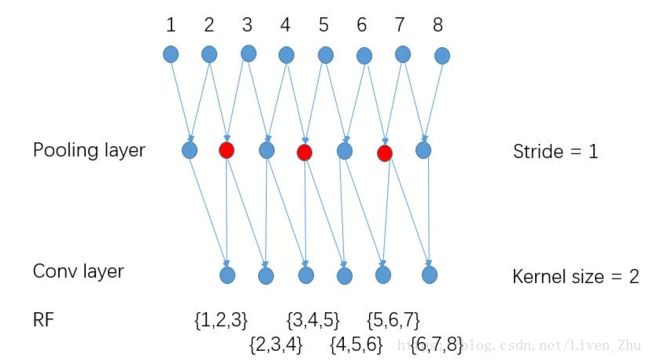
当将stride都设为1后，虽然输出数据的维度增大了，但是数据中每一个元素的感受域却减小了，由原来的4变为3。

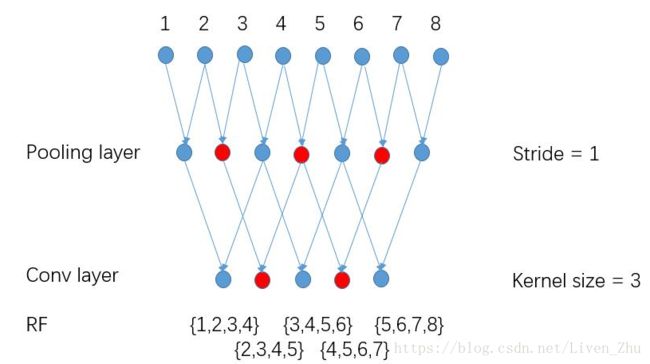
于是DeepLab在将所有层的stride都设为1后，采用基于稀疏卷积核的卷积来代替普通的卷积，这样做的优点是即增加了输出数据的维度，又保证了感受域大小不变，从而提高了语义分割的分辨率。

DeepLab v2:
v2在v1的基础上，又进行了进一步的优化。Multi-scale对模型变现的提升很大，而我们知道，感受域是指feature map上一个点能看到的原图的区域，那么如果有多个感受域，是不是相当于一种Multi-scale？出于这个思路，v2版本在v1的基础上增加了一个多感受域。具体看图可以很直观的理解。

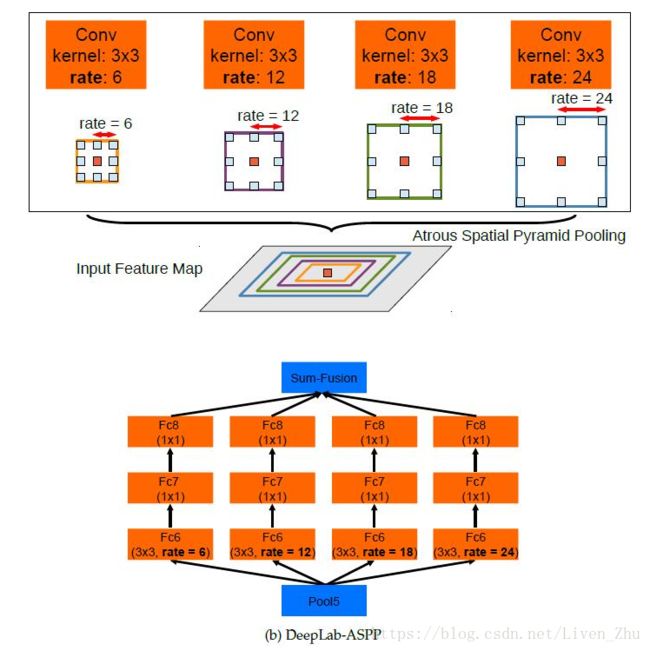
2.5 RefineNet

基于稀疏核的卷积也不是没有缺点，缺点就是会极大的增加计算量和需要的内存空间，因为稀疏核增加了参数的个数，使得要处理的数据维度增大。这就增大了获取更高分辨率分割图的成本。因此有学者提出了使用Encoder-Decoder架构的RefineNet。


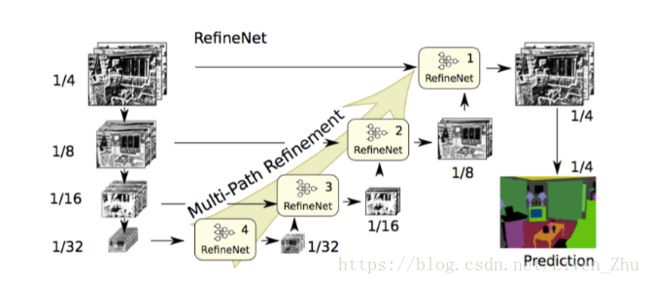
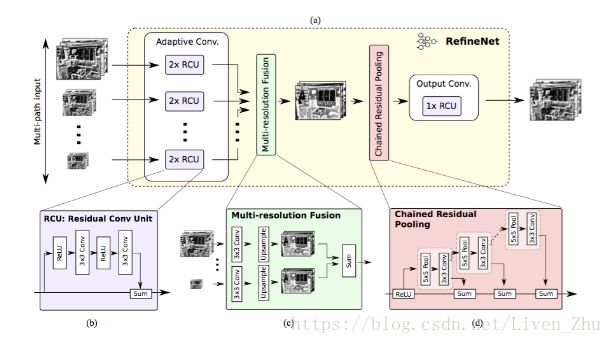
网络首先对图片输入进行处理，将原始图片做成不同的大小，分别输入到网络中，经过残差卷积网络后，得到具有多个分辨率的图，然后经过多分辨率融合网络，将多个分辨率图像进行融合，最后得到一个高分辨率的图片，最后经过残差池化和上采样，得到图片的分割图。

2.6 PSPNet

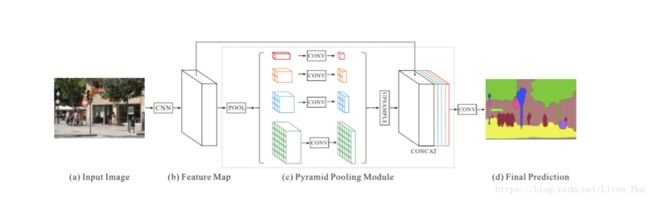
PSPNet采用ResNet对原始输入图像进行特征映射后，利用多个大小不同的并行池化层，得到多种规模的输出数据，然后再通过上采样过程，将维度小的输出数据映射到维度大的输出数据上，最后对所有的输出数据进行连接，再经过卷积层，得到最后的语义分割图。

2.7 Large Kernel Matters

语音分割同时需要分割对象的分割和分类，因此，FCNN并不完全适用于这种情况，相反，可以用具有很大kernel size的卷积。
具有很大kernel size的卷积具有更多的参数，因此需要更大的算力。因此这个模块在论文中也被叫做Global Convolutional Network（GCN）。
该网络的架构如下：

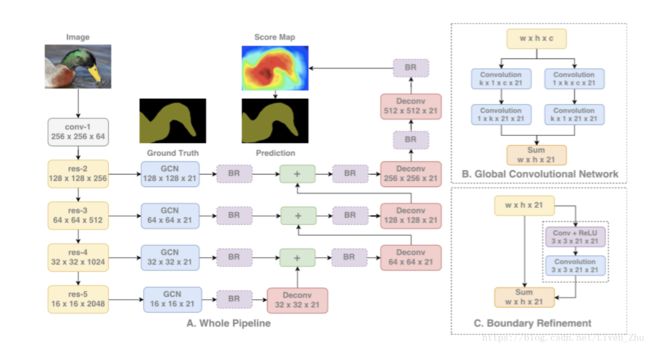
网络同样采用了多个并行结构，对不同尺寸规模的图像进行运算，然后再将多个图像进行融合，得到最后的分割图。

条件随机场（CRF）

最后再来说一下，用于训练上述网络的损失函数。语义分割模型采用条件随机场作为网络的损失函数。
在许多语义分割架构中，CNN 旨在最小化的损失函数是交叉熵损失。该目标函数度量的是预测像素概率分布（在所有类上）和实际像素概率分布的差异。

然而，对语义分割来说，交叉熵损失并不理想。因为对一张图来说，交叉熵损失是每一个像素损失的和，它并不鼓励邻近像素保持一致。因为交叉熵损失无法在像素间采用更高级的结构，所以交叉熵最小化的标签预测一般都是不完整或者是模糊的，它们都需要进行后续处理。

来自 CNN 的原始标签一般都是「缺失（patchy）」图像，在图像中有一些小区域的标签可能不正确，因此无法匹配其周围的像素标签。为了解决这种不连续性，我们可以用一种平滑的形式。我们需要确保目标占据图片中的连续区域，这样给定的像素和其周围像素的标签就是一样的。

为了解决这个问题，有一些架构使用了条件随机场（CRF），使用原始图像中像素的相似性重新精炼 CNN 的标签。

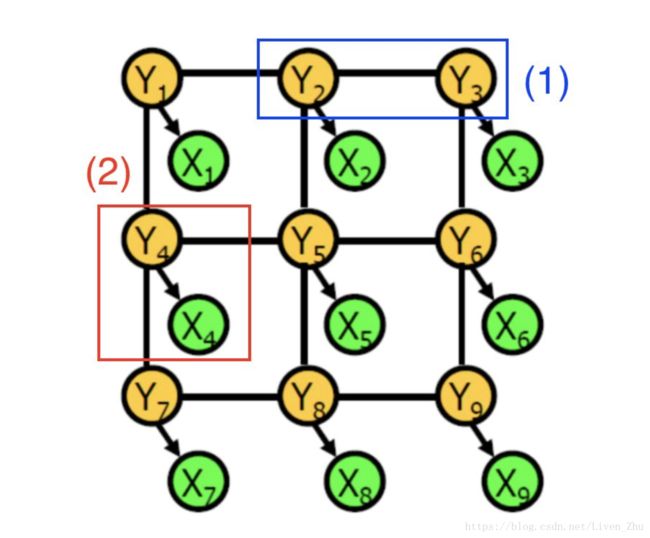
条件随机场是由随机变量组成的图，在这种情况下，每个顶点表示：

确定像素的 CNN 预测标签（绿色顶点 X_i）

确定像素的实际类别标签（黄色顶点 Y_i）

边会编码两类信息：

（1）蓝色：两个像素的实际类别，即它们之间的依赖关系

（2）红色：对于给定像素的 CNN 预测和实际标签之间的依赖关系

每个依赖性关系都具有势能，这是一个关于两个相关随机变量值的函数。例如，当相邻像素的实际目标标签相同时，第一类依存关系的势能较高。直观地讲，当目标标签是隐藏变量时，会根据概率分布产生可观察的 CNN 像素标签。

为了用 CRF 精炼标签，我们首先通过交叉验证用训练数据学习图模型的参数。然后，为了使概率 P（Y_1, Y_2, … Y_n | X_1, X_2,…X_n）最大化，对参数进行调整。CRF 的输出是原始图像像素的最终的目标标签。

实际上，CRF 图是完全连接的，也就意味着即使是从物理角度上讲相距很远的像素节点也可以共享边。这样的图有数十亿的边，从计算上讲难以进行精确处理。CRF 架构倾向于使用高效的近似技术进行处理。