GLSL中文手册

参考GitHub,传送门开启，嘛咪嘛咪哄！https://github.com/wshxbqq/GLSL-Card

• vertex shader（顶点着色器）：顶点着色器是一组指令代码，这组指令代码在顶点被渲染时执行。 同一时间内，只能激活一个顶点着色器。 每个源顶点着色器最多拥有128条指令（DirextX8.1），而在DirectX9，则可以达到256条。顶点着色器可以提高渲染场景速度。 用顶点着色器你可以做布类仿真，高级别动画，实时修改透视效果（比如水底效果），高级光亮（需要像素着色器支持）。
• fragment shader（片元着色器）：是另外一个非常重要的可编程着色器阶段。在DirectX中，片元着色器又被称为像素着色器(PixelShader),但片元着色器是个更合适的名字，因为此时片元并不是一个真正意义上的像素。
  片元着色器的输入是上一个阶段对顶点信息插值得到的结果，具体来说，是根据那些从顶点着色器中输出的数据插值得到的。而它的输出是一个或者多个颜色值。 这一阶段可以完成很多重要的渲染技术，最重要的技术之一就是纹理采样。为了在片元着色器中进行纹理采样。通常在顶点着色器阶段输出每个顶点的纹理坐标，然后经过光栅化阶段对三角形网格的3个顶点的纹理坐标进行插值后，就可以得到其覆盖的片元的纹理坐标了。
• framebuffer（帧缓冲器）：帧缓冲器是指计算机系统中专门用来存放正在合成或显示的图像的存储器。
• 法线：始终垂直于某平面的虚线。
  　　曲线的法线是垂直于曲线上一点的切线的直线，曲面上某一点的法线指的是经过这一点并且与该点切平面垂直的那条直线（即向量）。
  　　过入射点垂直于镜面的直线叫做法线。
  　　对于立体表面而言，法线是有方向的：一般来说，由立体的内部指向外部的是法线正方向，反过来的是法线负方向。
• 图元：图元，全称为图形输出原语(graphics output primitive)，是图形软件包中用来描述各种图形元素的函数，或简称为图元(primitive)。描述对象几何要素的输出图元一般称为几何图元。点的定位和直线段是最简单的几何图元。图元的名字为“entity”,翻译为中文有“图素”、“图元”、“实体”等称呼。
• 光栅化：光栅化阶段并不影响屏幕上每个像素的颜色值，而是产生一系列的数据信息，用来表述一个三角网格是怎么覆盖每个像素的。而每个片元就是负责存储这一系列数据。真正会对像素产生影响的阶段是下一个流水线阶段–逐片元操作(Per-FragmentOperations)。

基本类型

类型	说明
void	空类型，即不返回任何值
bool	布尔类型 tue,false
int	带符号的整数 sgned integer
float	带符号的浮点数 floating scalar
vec2,vec3,vec4	n维浮点向量 n-component floating point vector
bvec2,bvec3,bvec4	n维布尔向量 Boolean vector
ivec2,ivec3,ivec4	n维整数向量 signed integer vector
mat2,mat3,mat4	2x2,3x3,4x4 浮点数矩阵 float matrix
sampler2D	2D纹理 a 2D texture
samplerCube	盒纹理 cube mapped texture

基本结构和数组

类型	说明
结构	suct type-name{} 类似C语言中的 结构体
数组	float foo[3] glsl只支持1维数组，数组可以是结构体的成员

向量的分量访问

glsl中的向量（vec2,vec3,vec4)往往有特殊的含义，比如可能代表一个空间坐标（x,y,z,w),或者代表了一个颜色（r,g,b,a)，再者代表一个纹理坐标（s,t,p,q)所以glsl提供了一些更人性化的分量访问方式。
vector.xyzw 其中xyzw 可以任意组合
vector.rgba 其中rgba 可以任意组合
vector.stpq 其中stpq 可以任意组合

vec4 v=vec4(1.0,2.0,3.0,4.0);
float x=v.x;//1.0
float x1=v.r;//1.0
float x2=v[0];//1.0

vec3 xyz=v.xyz;//vec3(1.0,2.0,3.0)
vec3 xyz1=vec(v[0],v[1],v[2]);//vec3(1.0,2.0,3.0)
vec3 rgb=v.rgb;//vec3(1.0,2.0,3.0)
vec2 xyzw=v.xyzw;//vec4(1.0,2.0,3.0,1.0);
vec2 rgba=v.rgba;//vec4(1.0,2.0,3.0,4.0)

运算符

优先级（越小越高）	运算符	说明	综合性
1	()	聚组：a*(b+c)	N/A
2	[] () . ++ –	数组下标_[],方法参数_fun(arg1,arg2,arg3),属性访问_a.b_,自增、自减后缀++ a–_	L-R
3	++ – + - !	自增、自减前缀_++a --a_,正负号（一般正号不写）a,-a,取反_!false_	R-L
4	* /	乘除数学运算	L-R
5	+ -	加减数学运算	L-R
7	< > <= >=	关系运算符	L-R
8	== !=	相等性运算符	L-R
12	&&	逻辑与	L-R
13	^^	逻辑排他或（用处基本等于!=)	L-R

ps 左值与右值

左值：表示一个存储位置，可以是变量，也可以是表达式，但表达式最后的结果必须是一个存储位置。
右值：表示一个值，可以是一个变量或者表达式再或者纯粹的值。
操作符的优先级：决定含有多个操作符的表达式的求值顺序，每个操作的优先级不同。
操作符的结合性：决定相同优先级的操作符是从左到右计算，还是从右到左计算。

基础类型间的运算

glsl中，没有隐式类型转换，原则上glsl要求任何表达式左右两侧（l-value），（r-value)的类型必须一致，也就是说以下的表达式都是错的：

int a=2.0;//错误，r-value为false 而 l-vale 为 int，
int a=1.0+2;
float a=2;
float a=2.0+1;
bool a=0;
vec3 a=vec3(1.0,2.0,3.0)*2;

下面来分别说说可能遇到的情况

1.float与int
float与float，int与int之间是可以直接运算的，但float和int不行，他们需进行一次显式转换，即要么把float转成int：int（1.0），要么把int转成float（1），一下表达式都是正确的：

int a=int(2.0);
float a=float(2);

int a=int(2.0)*2+1;
float a=float(2)*6.0+2.3;

2.float与vec(向量）mat(矩阵)
vec,mat这些类型其实是由float复合而成的，当他们与float运算时，其实就是在一个分量上分别与float进行运算，这就是所谓的逐分量运算。glsl里大部分涉及vec,mat的运算都是逐分量运算，但也并不全是。下文中就会讲到特例。

逐分量运算是线性的，这就是说 vec 与 float 的运算结果是还是 vec.

int与vec，mat之间是不可运算的，因为vec和mat中的每一个分量都是float类型的。无法与int进行逐分量计算。

下面枚举了几种float与vec,mat运算的情况

vec3 a=vec3(1.0,2.0,3.0);
mat3m=mat3(1.0);
float s=10.0;
vec3 b=s*a;//vec3(10.0,20.0,30.0)
vec3 c=a*s;//vec3(10.0,20.0,30.0)
mat3 m2=s*m;//=mat3(10.0)
mat3 m3=m*s;//=mat3(10.0)

3.vec(向量)与vec(向量)
两向量间的运算首先要保证操作数的阶数都相同。否则不能计算。例如：vec3*vec2 vec4+vec3等等都是不行的。

它们的计算方式是操作数在同位置上的分量分别进行运算，其本质还是逐分量进行的，这和上面所说的float类型的逐分量运算可能有一点点差异，相同的是vec与vec运算结果还是vec，且阶数不变。

vec3 a=vec3(1.0,2.0,3.0);
vec3 b=vec3(0.1,0.2,0.3);
vec3 c=a+b;//=vec3(1.1，2.2，3.3）
vec3 d=a*b://=vec3(0.1,0.4,0.9)

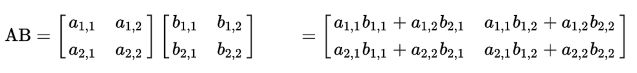
3.vec(向量)与mat(矩阵):
要保证操作数的阶数相同，且vec与mat间只存在乘法运算。
它们的计算方式和线性代数中的矩阵乘法https://jingyan.baidu.com/article/4ae03de3d2b8c13eff9e6b1e.html相同，不是逐分量运算。

vec2 v=vec2(10.,20.);
mat2 m=mat2(1.,2.,3.,4.);
vec2 w=m*v;//=vec2(1.*10.+3.*20.,2.*10.+4.*20.);
...
vec2 v=vec2(10.,20.);
mat2 m=mat2(1.,2.,3.,4.);
vec2 w=v*m;//=vec2(1.*10.+2.*20.,3.*10.+4.*20.)

向量与矩阵的乘法规则如下：


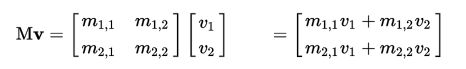
4.mat(矩阵)与mat(矩阵)
要保证操作数的阶数相同。
在mat与mat的运算中，除了乘法是线性代数中的矩阵乘法外。其余的运算任为逐分量运算。简单说就是只有乘法是特殊的，其余都和vec与vec运算类似。

mat2 a=mat2(1.,2., 3.,4.);
mat2 b=mat2(10.,20., 30.,40.);
mat2 c=a*b;//mat2(1.*10.+3.*20.,2.*10.+4.*20.,1.*30.+3.*40.,2.*30.+4.*40.);

mat2 d=a+b;//mat(1.+10.,2.+20.,3.+30.,4.+40);

矩阵乘法规则如下：

变量限定符：

修饰符	说明
none	(默认的可以省略）本地变量，可读可写，函数的输入参数既是这种类型
const	声明变量或函数的参数为只读类型
attribute	只能存在于vertex shader中，一般用于保存顶点或法线数据，它可以在数据缓冲区中读取数据
uniform	在运行时shader无法改变uniform变量，一般用来放置程序传递给shader的变换矩阵，材质，光照参数等等。
varying	主要负责在vertex和fragment之间传递变量

const:
和C语言类似，被const限定符修饰的变量初始化后不可变，除了局部变量，函数参数也可以使用const修饰符。但要注意的是结构变量可以用const修饰，但结构中的字段不行。

const变量必须在声明时就初始化const vec3 v3=vec3(0.,0.,0.)
局部变量只能使用const限定符。
函数参数只能使用const限定符。

struct light{
            vec4 color;
            vec3 pos;
            //const vec3 pos1;//结构中的字段不可用const修饰会报错。
            }；
 const light lgt=light(vec4(1.0),vec(3.0));//结构变量可以用const修饰

attribute：
attribute变量是全局且只读的，它只能在vertex shader中使用，只能与浮点数，向量或矩阵变量组合，一般attribute变量用来放置程序传递来的模型顶点，法线，颜色，纹理等数据它可以访问数据缓冲区（还记得_gl.vertexAttribPointer_这个函数吧）

attribute vec4 a_Position;

uniform:
uniform变量是全局且只读的，在整个shader执行完毕前其值不会改变，它可以和任意基本类型变量组合，一般我们使用uniform变量来放置外部程序传递来的环境数据（如点光源位置，模型的变换矩阵等等）这些数据在运行中显然是不需要被改变的。

uniform vec4 lightPosition；

varying：
varying类型变量是vertex shader与fragment shader之间的信使，一般我们在vertex shader中修改它然后在fragment shader使用它，但不能在fragment shader中修改它。

//顶点着色器
varying vec4 v_Color；
void main (){
           ...
           v_Color=vec4(1.,1.,1.,1.);
           }
//片元着色器
  ...
  varying vec4 v_Color;
  void main(){
          gl_FragColor=v_Color;
          }
          ...

要注意全局变量限制符只能为const、attribute、uniform和varying中的一个。不可复合。

函数参数限定符

函数的参数默认是以拷贝的形式传递的，也就是值传递，任何传递给函数参数的变量，其值都会被复制一份，然后再交给函数内部进行处理。我们可以为参数添加限定符来达到传递引用的目的，glsl中提供的参数限定符如下：

限定符	说明
< one:default >	默认使用in限定符
in	复制到函数中在函数中可读写
out	返回时从函数中复制出来
inout	复制到函数中并在返回时复制出来

in是函数参数的默认限定符，最终真正传入函数形参的其实是实参的一份拷贝。在函数中，修改in修饰的形参不会影响到实参变量本身。
out它的作用是向函数外部传递新值，out模式下传递进来的参数是write-only的（可写不可读）。就像是一个“坑位“，坑位中的值需要函数给他赋予。在函数中，修改out修饰的形参会影响到实参本身。
inoutinout下，形参可以被理解为是一个带值得“坑位”，及可读也可写，在函数中，修改inout修饰的形参会影响到实参本身。

glsl的函数

glsl允许在程序的最外部声明函数。函数不能嵌套，不能递归调用，且必须声明返回值类型（无返回值时声明为void）在其他方面glsl函数与c函数非常类似。

vec4 getPosition（）{
             vec4 v4=vec4（0.，0.，0.，1.）；
             return v4；
             }
void doubleSize（inout float size）{
              size=size*2.0；
              }
void main（）{
              float psize=10.0；
              doubleSize(psize);
              gl_Position=getPosition();
              gl_PointSize=psize;
              }

构造函数

glsl中变量可以在声明的时候初始化，float pSize=10.0也可以先声明然后等需要的时候在进行赋值。
聚合类型对象如（向量，矩阵，数组，结构）需要使用其构造函数来进行初始化。vec4 color=vec4（0.0，1.0，0.0，1.0）；

//一般类型
float pSize=10.0;
float pSize1;
pSize1=10.0;
...

//复合类型
vec4 color=vec4(0.0,1.0,0.0,1.0);
vec4 color1;
color1=vec4(0.0,1.0,0.0,1.0);
...

//结构
struct light{
          float intensity;
          vec3 position;
          };
light lighVar=light(3.0,vec3(1.0,2.0,3.0));

//数组
const float c[3]=float[3](5.0,7.2,1.1);

类型转换：

glsl可以使用构造函数进行显示类型转换，各值如下：

bool t=true;
bool f=false;

int a=int(t);//true转换为1或1.0
int a1 = int(f);//false转换为0或0.0

float b = float(t);
float b1 = float(f);

bool c = bool(0);//0或0.0转换为false
bool c1 = bool(1);//非0转换为true

bool d = bool(0.0);
bool d1 = bool(1.0);

精度限定

glsl在进行光栅化着色的时候，会产生大量的浮点数运算，这些运算可能是当前设备所不能承受的，所以glsl提供了3种浮点数精度，我们可以根据不同的设备来使用合适的精度。
在变量前面加上highp``mediump``lowp即可完成对该变量的精度声明。

lowp float color;
varying mediump vec2 Coord;
lowp ivec2 foo(lowp mat3);
highp mat4 m;

我们一般在片元着色器（fragment shader)最开始的地方加上precision mediump float;便设定了默认的精度。这样所有没有显示表明精度的变量 都会按照设定好的默认精度来处理。

如何确定精度

变量的精度首先是由精度限定符决定的，如果没有精度限定符，则要寻找其右侧表达式中，已经确定精度的变量，一旦找到，那么整个表达式都将在该精度下运行。如果找到多个，则选择精度较高的那种，如果一个都找不到，则使用默认或更大的精度类型。

uniform highp float h1;
highp float h2=2.3*4.7;//运算过程和结果都是高精度
mediump float m;
m =3.7*h1*h2;//运算过程 是高精度
h2 = m * h1; //运算过程 是高精度
m = h2 – h1; //运算过程 是高精度
h2 = m + m; //运算过程和结果都 是中等精度
void f(highp float p); // 形参 p 是高精度
f(3.3); //传入的 3.3是高精度

invariant关键字
由于shader在编译时 会进行一些内部优化，可能会导致同样的运算在不同的shader里结果不一定精确相等。这会引起一些问题，尤其是vertex shader向fragment shader传值的时候。所以我们需要使用invariant关键字来显示要求计算结果必须精确一致。当然我们也可使用 #pragma STDGL invariant(all)来命令所有输出变量必须精确一致,但这样会限制编译器优化程度,降低性能.

#pragma STDGL invariant(all) //所有输出变量为 invariant
invariant varying texCoord; //varying在传递数据的时候声明为invariant

限定符的顺序:
当需要用到多个限定符的时候要遵循以下顺序:
1.在一般变量中: invariant > storage > precision
2.在参数中: storage > parameter > precision
我们来举例说明:

invariant varying lowp float color; // invariant > storage > precision

void doubleSize(const in lowp float s){ //storage > parameter > precision
    float s1=s;
}

预编译指令:
以 # 开头的是预编译指令,常用的有:

#define #undef #if #ifdef #ifndef #else
#elif #endif #error #pragma #extension #version #line

比如 #version 100 他的意思是规定当前shader使用 GLSL ES 1.00标准进行编译,如果使用这条预编译指令,则他必须出现在程序的最开始位置.
内置的宏:
_LINE_:当前源码中的行号。
_VERSION_:一个整数，制定当前的glsl版本 比如 100 ps:100=v1.00
GL_ES:如果当前是在OPGL ES环境中运行则GL_ES被设置成1，一般用来检查当前环境是不是OPENGL ES.
GL_FRAGMENT_PRECISION_HIGH:如果当前系统glsl的片元着色器高浮点精度，则设置为1.一般用于检查着色器精度。
实例：
1.如何通过判断系统环境，来选择合适的精度：

#ifdef GL_ES //
#ifdef GL_FRAGMENT_PRECISION_HIGH
precision highp float;
#else
precision mediump float;
#endif
#endif

2.自定义宏：

#define NUM 100
#if NUM==100
#endif

内置的特殊变量

glsl程序使用一些特殊的内置变量与硬件进行沟通。他们大致分成两种 一种是input类型，它负责向硬件（渲染管线）发送数据。另一种是output类型，负责向程序回传数据，以便编程时需要。
在vertex shader中：
output类型的内置变量：

变量	说明	单位
highp vec4 gl_Position;	gl_Position放置顶点左边信息	vec4
mediump float gl_PointSize	gl_PointSize需要绘制点的大小，（只在gl.POINTS模式下有效）	float

在fragment shader中：
input类型的内置变量：

变量	说明	单位
mediump vec4 gl_FragCoord;	片元在framebuffer画面的相对位置	vec4
bool gl_FrontFacing	标志当前图元是不是正面图元的一部分	bool
mediump vec2 gl_PointCoord`;	经过插值计算后的纹理坐标，点的范围是0.0到1.0	vec2

output类型的内置变量：

变量	说明	单位
mediump vec4 gl_FragColor;	设置当前片点的颜色	vec4 RGBA color
mediump vec4 `gl_FragData[n]	设置当前片点的颜色，使用glDrawBuffers数据数组	vec4 RGBA color

内置的常亮

glsl提供了一些内置的常量,用来说明当前系统的一些特性. 有时我们需要针对这些特性,对shader程序进行优化,让程序兼容度更好.
在vertex shader中：
1.const mediump int gl_MaxVertexAttribs>=8
gl_MaxVertexAttribs表示在vertex shader中可用的最大attribute（属性）数。这个值的大小取决于OpenGL ES在某设备上的具体实现，不过最低不能小于8个。
2.const mediump int gl_MaxVertexUniformVectors>=128
gl_MaxVertexUniformVectors 表示在vertex shader(顶点着色器)中可用的最大uniform vectors数. 这个值的大小取决于 OpenGL ES 在某设备上的具体实现,
不过最低不能小于 128 个.
3.const mediump int gl_MaxVaryingVectors >= 8
gl_MaxVaryingVectors 表示在vertex shader(顶点着色器)中可用的最大varying vectors数. 这个值的大小取决于 OpenGL ES 在某设备上的具体实现,
不过最低不能小于 8 个.
4.const mediump int gl_MaxVertexTextureImageUnits >= 0
gl_MaxVaryingVectors 表示在vertex shader(顶点着色器)中可用的最大纹理单元数(贴图). 这个值的大小取决于 OpenGL ES 在某设备上的具体实现,
甚至可以一个都没有(无法获取顶点纹理)
5.const mediump int gl_MaxCombinedTextureImageUnits >= 8
gl_MaxVaryingVectors 表示在 vertex Shader和fragment Shader总共最多支持多少个纹理单元. 这个值的大小取决于 OpenGL ES 在某设备上的具体实现,不过最低不能小于 8 个.
在 fragment Shader 中:
1.const mediump int gl_MaxTextureImageUnits >= 8
gl_MaxVaryingVectors 表示在 fragment Shader(片元着色器)中能访问的最大纹理单元数,这个值的大小取决于 OpenGL ES 在某设备上的具体实现,
不过最低不能小于 8 个.
2.const mediump int gl_MaxFragmentUniformVectors >= 16
gl_MaxFragmentUniformVectors 表示在 fragment Shader(片元着色器)中可用的最大uniform vectors数,这个值的大小取决于 OpenGL ES 在某设备上的具体实现,
不过最低不能小于 16 个.
3.const mediump int gl_MaxDrawBuffers = 1
gl_MaxDrawBuffers 表示可用的drawBuffers数,在OpenGL ES 2.0中这个值为1, 在将来的版本可能会有所变化.
glsl中还有一种内置的uniform状态变量, gl_DepthRange 它用来表明全局深度范围.
结构如下:

struct gl_DepthRangeParameters {
 highp float near; // n
 highp float far; // f
 highp float diff; // f - n
 };
 uniform gl_DepthRangeParameters gl_DepthRange;

除了 gl_DepthRange 外的所有uniform状态常量都已在glsl 1.30 中废弃.
流控制
glsl的流控制和c语言非常相似,这里不必再做过多说明,唯一不同的是片段着色器中有一种特殊的控制流discard.使用discard会退出片段着色器，不执行后面的片段着色操作。片段也不会写入帧缓冲区。

for (l = 0; l < numLights; l++)
{
    if (!lightExists[l]);
        continue;
    color += light[l];
}
...

while (i < num)
{
    sum += color[i];
    i++;
}
...

do{
    color += light[lightNum];
    lightNum--;
}while (lightNum > 0)


...

if (true)
    discard;

内置函数库

glsl提供了非常丰富的函数库,供我们使用,这些功能都是非常有用且会经常用到的. 这些函数按功能区分大改可以分成7类:

通用函数:
下文中的 类型 T可以是 float, vec2, vec3, vec4,且可以逐分量操作.

方法	说明
T abs(T x)	返回x的绝对值
T Sign(T x)	比较X与0的值，大于，等于，小于 分别返回1.0，0.0，-1.0
T floor(T X)	返回<=x的最大整数
T ceil(T x)	返回>=等于x的最小整数
T fract(T x)	获取x的小数部分
T mod(T x, T y) 、T mod(T x, float y)	取x,y的余数
T min(T x, T y) 、 T min(T x, float y)	取x,y的最小值
T max(T x, T y) 、 T max(T x, float y)	取x,y的最大值
T clamp(T x, T minVal, T maxVal) 、T clamp(T x, float minVal,float maxVal)	min(max(x, minVal), maxVal),返回值被限定在 minVal,maxVal之间
T mix(T x, T y, T a) 、T mix(T x, T y, float a)	取x,y的线性混合,x*(1-a)+y*a
T step(T edge, T x) 、 T step(float edge, T x)	如果 x
T smoothstep(T edge0, T edge1, T x) 、 T smoothstep(float edge0,float edge1, T x)	如果xedge1返回1.0, 否则返回Hermite插值

角度&三角函数:
下文中的 类型 T可以是 float, vec2, vec3, vec4,且可以逐分量操作.

方法	说明
T radians(T degrees)	角度转弧度
T degrees(T radians)	弧度转角度
T sin(T angle)	正弦函数,角度是弧度
T cos(T angle)	余弦函数,角度是弧度
T tan(T angle)	正切函数,角度是弧度
T asin(T x)	反正弦函数,返回值是弧度
T acos(T x)	反余弦函数,返回值是弧度
T atan(T y, T x)、 T atan(T y_over_x)	反正切函数,返回值是弧度

指数函数:
下文中的 类型 T可以是 float, vec2, vec3, vec4,且可以逐分量操作.

方法	说明
T pow(T x, T y)	返回x的y次幂 xy
T exp(T x)	返回x的自然指数幂 ex
T log(T x)	返回x的自然对数 ln
T exp2(T x)	返回2的x次幂 2x
T log2(T x)	返回2为底的对数 log2
T sqrt(T x)	开根号 √x
T inversesqrt(T x)	先开根号,在取倒数,就是 1/√x

几何函数:
下文中的 类型 T可以是 float, vec2, vec3, vec4,且可以逐分量操作.

方法	说明
float length(T x)	返回矢量x的长度
float distance(T p0, T p1)	返回p0 p1两点的距离
float dot(T x, T y)	返回x y的点积
vec3 cross(vec3 x, vec3 y)	返回x y的叉积
T normalize(T x)	对x进行归一化,保持向量方向不变但长度变为1
T faceforward(T N, T I, T Nref)	根据 矢量 N 与Nref 调整法向量
T reflect(T I, T N)	返回 I - 2 * dot(N,I) * N, 结果是入射矢量 I 关于法向量N的 镜面反射矢量
T refract(T I, T N, float eta)	返回入射矢量I关于法向量N的折射矢量,折射率为eta

矩阵函数:
mat可以为任意类型矩阵.

方法	说明
mat matrixCompMult(mat x, mat y)	将矩阵 x 和 y的元素逐分量相乘

向量函数:
下文中的 类型 T可以是 vec2, vec3, vec4, 且可以逐分量操作.
bvec指的是由bool类型组成的一个向量:

vec3 v3= vec3(0.,0.,0.);
vec3 v3_1= vec3(1.,1.,1.);
bvec3 aa= lessThan(v3,v3_1); //bvec3(true,true,true)

方法	说明
bvec lessThan(T x, T y)	逐分量比较x < y,将结果写入bvec对应位置
bvec lessThanEqual(T x, T y)	逐分量比较 x <= y,将结果写入bvec对应位置
bvec greaterThan(T x, T y)	逐分量比较 x > y,将结果写入bvec对应位置
bvec greaterThanEqual(T x, T y)	逐分量比较 x >= y,将结果写入bvec对应位置
bvec equal(T x, T y) 、 bvec equal(bvec x, bvec y)	逐分量比较 x == y,将结果写入bvec对应位置
bvec notEqual(T x, T y) 、 bvec notEqual(bvec x, bvec y)	逐分量比较 x!= y,将结果写入bvec对应位置
bool any(bvec x)	如果x的任意一个分量是true,则结果为true
bool all(bvec x)	如果x的所有分量是true,则结果为true
bvec not(bvec x)	bool矢量的逐分量取反

纹理查询函数:
图像纹理有两种 一种是平面2d纹理,另一种是盒纹理,针对不同的纹理类型有不同访问方法.
纹理查询的最终目的是从sampler中提取指定坐标的颜色信息. 函数中带有Cube字样的是指 需要传入盒状纹理. 带有Proj字样的是指带投影的版本.
以下函数只在vertex shader中可用:

vec4 texture2DLod(sampler2D sampler, vec2 coord, float lod);
vec4 texture2DProjLod(sampler2D sampler, vec3 coord, float lod);
vec4 texture2DProjLod(sampler2D sampler, vec4 coord, float lod);
vec4 textureCubeLod(samplerCube sampler, vec3 coord, float lod);

以下函数只在fragment shader中可用:

vec4 texture2D(sampler2D sampler, vec2 coord, float bias);
vec4 texture2DProj(sampler2D sampler, vec3 coord, float bias);
vec4 texture2DProj(sampler2D sampler, vec4 coord, float bias);
vec4 textureCube(samplerCube sampler, vec3 coord, float bias);

在 vertex shader 与 fragment shader 中都可用:

vec4 texture2D(sampler2D sampler, vec2 coord);
vec4 texture2DProj(sampler2D sampler, vec3 coord);
vec4 texture2DProj(sampler2D sampler, vec4 coord);
vec4 textureCube(samplerCube sampler, vec3 coord);

官方的shader范例:

下面的shader如果你可以一眼看懂,说明你已经对glsl语言基本掌握了.
Vertex Shader:

uniform mat4 mvp_matrix; //透视矩阵 * 视图矩阵 * 模型变换矩阵
uniform mat3 normal_matrix; //法线变换矩阵(用于物体变换后法线跟着变换)
uniform vec3 ec_light_dir; //光照方向
attribute vec4 a_vertex; // 顶点坐标
attribute vec3 a_normal; //顶点法线
attribute vec2 a_texcoord; //纹理坐标
varying float v_diffuse; //法线与入射光的夹角
varying vec2 v_texcoord; //2d纹理坐标
void main(void)
{
 //归一化法线
 vec3 ec_normal = normalize(normal_matrix * a_normal);
 //v_diffuse 是法线与光照的夹角.根据向量点乘法则,当两向量长度为1是 乘积即cosθ值
 v_diffuse = max(dot(ec_light_dir, ec_normal), 0.0);
 v_texcoord = a_texcoord;
 gl_Position = mvp_matrix * a_vertex;
}

Fragment Shader:

precision mediump float;
uniform sampler2D t_reflectance;
uniform vec4 i_ambient;
varying float v_diffuse;
varying vec2 v_texcoord;
void main (void)
{
 vec4 color = texture2D(t_reflectance, v_texcoord);
 //这里分解开来是 color*vec3(1,1,1)*v_diffuse + color*i_ambient
 //色*光*夹角cos + 色*环境光
 gl_FragColor = color*(vec4(v_diffuse) + i_ambient);
}