神经网络与深度学习系列 - 梯度下降与随机梯度下降

神经网络与深度学习系列文章将作为于Michael Mielsen的《Nerual Networks and Deep Learning》一书的学习笔记，记录要点。这本书内容的开展方式非常棒：以原理为导向，通过攻克一个具体的问题“识别手写数字”，深入浅出的介绍神经网络与深度学习的基本理论。通过本书的学习可以在自己脑海中先构建一套完整的神经网络知识“骨架”，之后再通过其他方面学习将“羽翼”填充起来，逐步学习神经网络。

感知机

第一节介绍一种被称为 感知机 的神经元。感知机的基本结构如下：

一个感知机接受二进制输入 $x_1,x_2.....$,并产生一个 二进制输出 $output$. 上图感知机有三个输入$x_1,x_2,x_3$。权重$w_1,w_2.....$表示相应输入对于输出的重要程度。另一个感知机参数为阈值threshold，感知机的输出由输入的加权总和与阈值的大小关系决定，如下为感知机的基本代数模型：

可以将感知机作为依据权重和阈值来做出决定的设备。通过将${\sum }_j{w}_j{x}_j$改写成点乘$w\cdot x$来简化代数模型，其中$w$和$x$分别对应权重向量和输入向量，并且令偏置$b=-threshold$代替阈值，一个感知机将依据权重和偏置来做出决策。那么感知机模型可以重写如下：

假设我们有个两个输入的感知机，每个权重为-2，整体偏置为3，如下所示：

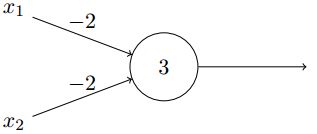
根据感知机模型，当我们输入$x_1=0,x_2=0$输出为1；当我们输入$x_1=0,x_2=1$输出为1；当我们输入$x_1=1,x_2=0$输出为1；当我们输入$x_1=1,x_2=1$输出为0.如此我们的感知机实现了一个与非门。与非门为通用电路，以上例子显示我们可以用感知机来构建任何运算。

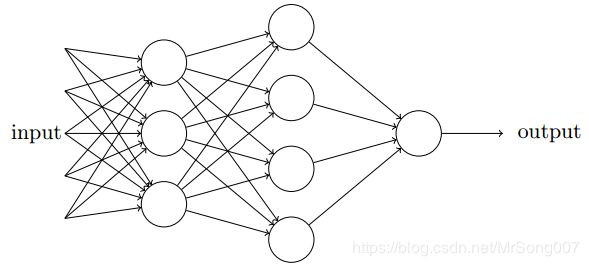
上图为一个感知机网络，第一层感知机可以做出3个简单的决定（假设一个输出为一个决定），第二层感知机权衡第一层感知机的决策结果可以做出更复杂和抽象的决定，第三层感知机权衡第二层感知机的决策结果可以做出更加复杂巧妙的决定。
同时利用感知机还有一个特点：我们可以设计学习算法，自动调整神经元的权重和偏置，这种调整可以响应外部的刺激，学习解决运算问题，然而这些问题直接用传统的电路设计是很难完成的。

S型神经元

学习算法听起来非常好，那么我们该如何给一个神经网络设计这样的算法呢？如果对权重（或者偏置）的微小的改动能够仅仅引起输出的微小变化，那我们可以利⽤这⼀事实来缓慢调节权重和偏置，让我们的⽹络能够表现得像我们想要的那样。显然感知机不能满足这一要求。

1. S型神经元定义：
在这里引出一种新的人工神经元 “S型神经元”。 S 型神经元和感知机类似，但是经过修改后，权重和偏置的微小改动只引起输出的微小变化。不同于感知机的输入只能是二进制输入，S型神经元的输入可以取任意值；但类似感知机，S型神经元对每个输入都有权重$w_1,w_2,...$和一个总的偏置$b$, 输出也不同于感知机只能是二进制输出，S型神经元的输出为 $\sigma (w\cdot x+b)$,其中 $\sigma$ 被称为S型函数（或逻辑函数），S型函数的定义为：

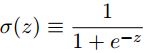
2. 对比S型神经元与感知机的相似性：
假设$z=w\cdot x+b$是一个很大的正数，$\sigma (z)\approx 1$；
假设$z=w\cdot x+b$是一个很大的负数，$\sigma (z)\approx 0$；
所以当S型神经元在$w\cdot x+b$ 取极大或极小的情况下行为近似于一个感知机。只有在$w\cdot x+b$ 取中间值时，S型神经元与感知机模型有较大的偏离；

S型函数的形状：

阶跃函数的形状：

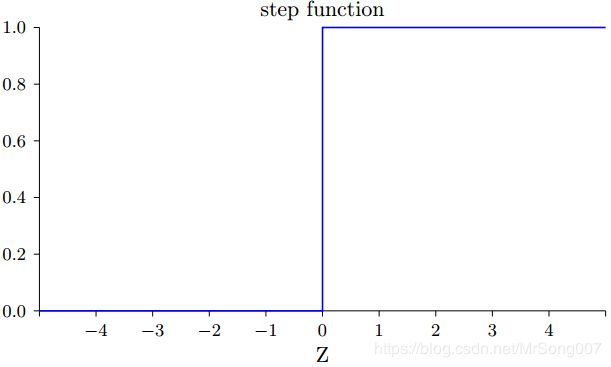
通过对比阶跃函数和S型函数形状，S型函数可以看成是阶跃函数的平滑版本，也就是说S型神经元是感知机的平滑版本。S型函数的平滑特性正是其关键特性，意味着: 权重的微小变化$\Delta w_j$和偏置的微小变化$\Delta b$，会从神经元产生一个微小的输出变化$\Delta output$,根据微积分原理 $\Delta output$可以很好的近似表示为：

神经网络的架构

假设我们有如下网络：

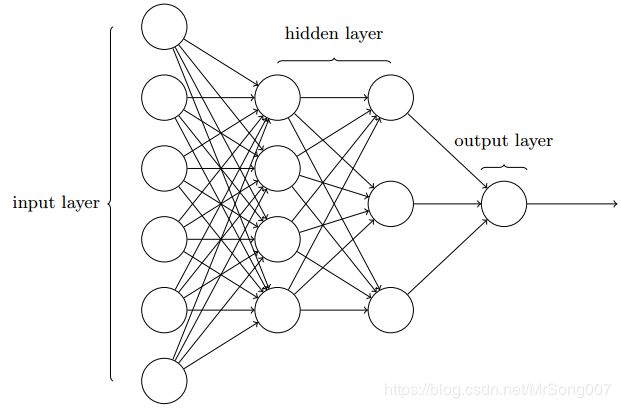
这个网络最左边的为输入层，其中的而神经元称为输入神经元，最右边的为输出层，其中的神经元称为输出神经元，中间的称为隐藏层。由于某些历史原因，有多个隐藏层的网络有时也被称为多层感知机（虽然网络是由S型神经元而不是感知机构成）。以上一层的输出作为下一层的输入的神经网络都被称为前馈神经网络。

设计一个识别手写数字的网络

我们使用一个三层神经网络来识别单个数字：

网络的输出输出层比较纯粹，手写数字的图像尺寸为28×28，那么输入层就包含784=28×28个神经元；网络的输出层包含10个神经元，如果第一个神经元激活，即输出>0.5，那么表示网络认为数字是一个0，如果第二个神经元被激活，表示网络认为数字是一个1，以此类推；网络的隐藏层使用15个神经元。

梯度下降算法

现在我们有设计好的神经网络，另外需要的第一个东西为训练数据集，采用MNIST数据集，其中灰度图像大小都是28×28，将MNIST数据分成两部分，第一部分包含60000张用于训练，第二部分包含10000张用于测试评估神经网络的学习成果。

我们希望设计一个算法，能够找到最佳权重和偏置，使得真实值$y$能够拟合所有的训练输入$x$，为了量化这个目标，定义一个代价函数：

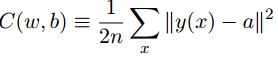
其中$w$和$b$分别表示网络中所有权重和偏置的集合，代价函数是$w$和$b$的函数。$n$为训练输入数据的个数，$a$为输入为$x$时网络预测输出的向量，$y(x)$为对应$x$的实际输出。但代价函数越小，意味着在当前学习算法找到的权重与偏置下，输出$a$与$y(x)$越接近，那么我们的网络就能很好的工作；所以我们的目的是找到让代价函数尽可能小的权重与偏置。这就是梯度下降算法的目的。

---

为了解释梯度下降算法，我们先假设$C(v)$是一个有两个变量 $v_1$ 和 $v_2$ 的函数,我们希望找到 $v_1$ 和 $v_2$ 的值使得$C(v)$取最小值，$C(v)$图形如下：

若变量 $v_1$ 和 $v_2$分别发生了很小的变化，根据微积分,$C$将有如下变化：

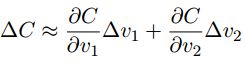
用向量表示$\Delta v=（\Delta v_1,\Delta v_2{）}^T$, $\nabla C$表示梯度向量，$\nabla C={\left(\frac{\partial C}{\partial v_1},\frac{\partial C}{\partial v_2}\right)}^T$,那么$\Delta C$就可以表示成：

若要找到找到 $v_1$ 和 $v_2$ 的值使得$C(v)$取最小值，每次 $v_1$ 和 $v_2$引起的$C$的变化$\Delta C$都应该为负。我们假设$\Delta v=-\eta \nabla C$,$\eta$是个很小的正数，称为学习率， 那么$\Delta C=-\eta {\Vert \nabla C\Vert }^2$一定是不大于0. 若我们一直按照$\Delta v=-\eta \nabla C$的规则去改变$v$，$C$就会一直减小，不会增加。

上面的过程复述一遍，若我们重复运用更新规律：

$C$就会一直减小，直到最小值。该更新规则就称为梯度下降算法。

---

返回到我们的代价函数，应用梯度下降的更新策略，我们得到：

随机梯度下降

我们的代价函数为

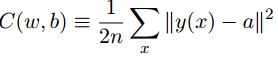
可以重写为：$C=\frac{1}{n}{\sum }_x{C}_x$,其中每个训练样本代价$C_x=\frac{{\Vert y(x)-a\Vert }^2}{2}$, 在实际应用中，需要为每个训练输入$x$单独计算梯度值$\nabla C_x$,然后求平均值$\nabla C=\frac{1}{n}{\sum }_x\nabla C_x$, 但训练输入的数量过大的时候花费时间很长，学习过程相当缓慢。 随机梯度下降算法是通过随机选取销量训练输入样本来计算$\nabla C_x$,进而估算出$\nabla C$ ,以此加速计算过程。具体过程如下：

随机选取小量的$m$个训练输入来工作，标记为$X_1,X_2,....X_m$,称之为小批量数据，但样本数量$m$足够大，$\nabla C_{x_j}$的平均值大致等于整个$\nabla C_x$的平均值，即：

由此可以得到仅仅通过随机选取的小批量数据的梯度来估计整体的梯度：

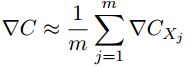
那么随机梯度下降的更新策略就可以更新如下：

其中的求和符号是在当前像批量数据中进行的，之后再挑选另一组进行更新策略，知道用完所有训练输入，该过程称之为一个训练迭代期。然后会开始一个新的迭代期。我们实际关心的是在使$C$下降的方向上移动，并不需要找到精确的下降最快的方向(梯度)，所以随机梯度下降算法来近似是合理的。

本系列的下一节将介绍 反向传播算法。