哈夫曼树的实现(构建、遍历)(附C++详细实现代码)
哈夫曼树
带权路径长度: 设二叉树有n个带权值的叶子结点,从根节点到各个叶子结点的路径长度与相应叶子结点权值的乘积之和叫做二叉树的带权路径长度。
哈夫曼树的定义:带权路径长度最小的二叉树(也称最优二叉树)
哈夫曼树的构建思路:
- 1、以权值分别为W1,W2...Wn的n各结点,构成n棵二叉树T1,T2,...Tn并组成森林 S={T1,T2,...Tn},其中每棵二叉树 Ti仅有一个权值为 Wi的根结点;
- 2、在S中选取两颗权值最小的树min_1,min_2,将他们的权值相加,生成一个新的树(权值为刚才的min_1,min_2的权值之和),然后将新的这棵树放回到S中去,将刚才那两颗树min_1和min_2删掉。
- 3、重复2、3操作,知道S只剩下一棵树为止。这棵树即哈夫曼树。
代码实现:用顺序存储结构比较简单,
先分析一下,原本有n个树,最后只剩下一颗,也就是进行了n-1次合并操作,新生成了n-1个节点,也就是我们的存储空间至少2*n-1个来存储
哈夫曼树的抽象类型定义:
为了判断树节点是否在哈夫曼树中,我们用parents来辨别,初始化全为-1,当该节点插入到哈夫曼树中的时候,parents的值为该节点的双亲节点在数组的下标。
class HaFuman {
public:
int weight;//权重
int parents;//树的双亲节点
int lchird;
int rchild;
HaFuman() {//初始化全部为0
this->parents = -1;
this->lchird = -1;
this->rchild = -1;
}
};
具体代码实现思路:
- 1、首先创建一个空间长度为2n-1的数组hafuman,然后先将给定的n个带权值的叶子节点放到数组中。
- 2、从hafuman树中挑选两个权值最小的两棵树,返回其在数组中的下标 min_1,min_2。然后将这两颗树组成一颗新的树节点放到n+1,然后将最小的两棵树的双亲设置为n+1,新的树节点的左右孩子设置为min_1,min_2。
- 3、循环操作2、知道处理到最后一个树即新生成的树放到下标为2n-1时停止,此时剩下一颗树的双亲为-1,这棵树即哈夫曼树。
创建哈夫曼树函数
void creathaFuMan(HaFuman* hafuman,int n,int a[]) {
for (int i = 0; i <= 2*n-1; i++) {
//构造只有根节点的哈夫曼树
hafuman[i].weight = a[i];
}
//进行n-1次的合并
for (int i = n; i < 2*n - 1; i++) {//n-1次的合并操作
int min_1 = 0;
int min_2 = 0;
selectMin_2(hafuman, i, min_1, min_2);//此时min_1为最小权重的森林的节点,min_2为次小
//找到最小的两个节点之后,我们需要将这两个位置的权重相加
hafuman[i].weight = hafuman[min_1].weight + hafuman[min_2].weight;
hafuman[i].lchird = min_1;
hafuman[i].rchild = min_2;
hafuman[min_1].parents = i;
hafuman[min_2].parents = i;
}
}
其中selectMin_2()函数就是取两个最小权值的树的下标,实现如下:
void selectMin_2(HaFuman* hafuman, int n, int &min_1, int &min_2) {
for (int i = 0; i < n; i++) {
if (hafuman[i].parents == -1) { //先找那些还没有归为一颗树的节点
min_1 = i;
break;
}
}
for (int i = 0; i < n; i++) {
if (hafuman[i].parents == -1 && hafuman[i].weight < hafuman[min_1].weight) {
min_1 = i;
}
}
for (int i = 0; i < n; i++) {
if (hafuman[i].parents == -1 && i != min_1) {
min_2 = i;
break;
}
}
for (int i = 0; i < n; i++) {
if (hafuman[i].parents == -1 && hafuman[min_2].weight >
hafuman[i].weight && i != min_1) {
min_2 = i;
}
}
}
遍历函数:
遍历的时候需要借助一下头文件
这个头文件声明了一些常用的流操作,例如 left向左对齐,例如right向右对齐,还有setw()是设置宽度的.
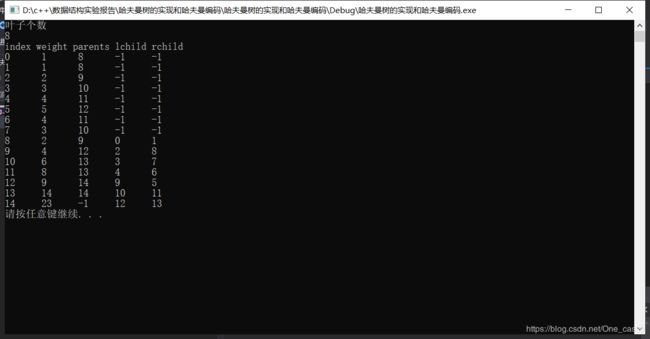
void printHaFuMan(HaFuman* hafuman, int n) {
cout << "index weight parents lchild rchild" << endl;
cout << left;
for (int i = 0; i < 2 * n - 1; i++) {
cout << setw(6) << i << " ";
cout <最后是main函数
#include
#include"HaFuMan.h"
using namespace std;
int main() {
int n;
cout << "叶子个数" << endl;
cin >> n;
int a[8] = {1,1,2,3,4,5,4,3};
//申请一个长度为2n的哈夫曼结构数组
HaFuman* hafuman = new HaFuman[2*n-1];
creathaFuMan(hafuman, n, a);
printHaFuMan(hafuman, n);
system("pause");
return 0;
}
完整代码如下
//HaFuMan.h
//哈夫曼树的结构
class HaFuman {
public:
int weight;//权重
int parents;//树的双亲节点
int lchird;
int rchild;
HaFuman() {//初始化全部为0
this->parents = -1;
this->lchird = -1;
this->rchild = -1;
}
};
//找到最小权重的两个下标
void selectMin_2(HaFuman* hafuman, int n, int &min_1, int &min_2) {
for (int i = 0; i < n; i++) {
if (hafuman[i].parents == -1) { //先找那些还没有归为一颗树的节点
min_1 = i;
break;
}
}
for (int i = 0; i < n; i++) {
if (hafuman[i].parents == -1 && hafuman[i].weight < hafuman[min_1].weight) {
min_1 = i;
}
}
for (int i = 0; i < n; i++) {
if (hafuman[i].parents == -1 && i != min_1) {
min_2 = i;
break;
}
}
for (int i = 0; i < n; i++) {
if (hafuman[i].parents == -1 && hafuman[min_2].weight >
hafuman[i].weight && i != min_1) {
min_2 = i;
}
}
}
//哈夫曼树的构建
void creathaFuMan(HaFuman* hafuman,int n,int a[]) {
for (int i = 0; i <= 2*n-1; i++) {
//构造只有根节点的哈夫曼树
hafuman[i].weight = a[i];
}
//进行n-1次的合并
for (int i = n; i < 2*n - 1; i++) {//n-1次的合并操作
int min_1 = 0;
int min_2 = 0;
selectMin_2(hafuman, i, min_1, min_2);//此时min_1为最小权重的森林的节点,min_2为次小
//找到最小的两个节点之后,我们需要将这两个位置的权重相加
hafuman[i].weight = hafuman[min_1].weight + hafuman[min_2].weight;
//我们对左右孩子的大小进行限制一下:权值比较小的在左边,大的在右边,相等的话,由于找的时候是按顺序找的,所以真实叶子也为min_1
if (min_1 <= min_2) {
hafuman[i].lchild = min_1;
hafuman[i].rchild = min_2;
}
else{
hafuman[i].lchild = min_2;
hafuman[i].rchild = min_1;
}
hafuman[min_1].parents = i;
hafuman[min_2].parents = i;
}
}
//输出构建的哈夫曼树
void printHaFuMan(HaFuman* hafuman, int n) {
cout << "index weight parents lchild rchild" << endl;
cout << left;
for (int i = 0; i < 2 * n - 1; i++) {
cout << setw(6) << i << " ";
cout <#include
#include"HaFuMan.h"
using namespace std;
int main() {
int n;
cout << "叶子个数" << endl;
cin >> n;
int a[8] = {1,1,2,3,4,5,4,3};
//申请一个长度为2n的哈夫曼结构数组
HaFuman* hafuman = new HaFuman[2*n-1];
creathaFuMan(hafuman, n, a);
printHaFuMan(hafuman, n);
system("pause");
return 0;
}