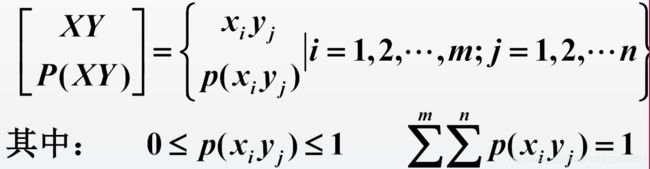香农密码理论汇总:熵理论
ref by https://www.wikiwand.com/zh-hans/熵_(信息论)
信息和熵
在信息论中,熵(英语:entropy)是接收的每条消息中包含的信息的平均量,又被称为信息熵、信源熵、平均自信息量。这里,“消息”代表来自分布或数据流中的事件、样本或特征。(熵最好理解为不确定性的量度而不是确定性的量度,因为越随机的信源的熵越大。)来自信源的另一个特征是样本的概率分布。这里的想法是,比较不可能发生的事情,当它发生了,会提供更多的信息。由于一些其他的原因,把信息(熵)定义为概率分布的对数的相反数是有道理的。事件的概率分布和每个事件的信息量构成了一个随机变量,这个随机变量的均值(即期望)就是这个分布产生的信息量的平均值(即熵)。熵的单位通常为比特,但也用Sh、nat、Hart计量,取决于定义用到对数的底。
采用概率分布的对数作为信息的量度的原因是其可加性。例如,投掷一次硬币提供了1 Sh的信息,而掷m次就为m位。更一般地,你需要用log2(n)位来表示一个可以取n个值的变量。
信息实际上就是一组随机变化的值,本质上就是对不确定信息的消除.以及相当重要的一点,信息的可加性.
自信息量
在信息论中,自信息(英语:self-information),由克劳德·夏农提出,是与概率空间中的单一事件或离散随机变量的值相关的资讯量的量度。它用信息的单位表示,例如 bit、nat或是hart,使用哪个单位取决于在计算中使用的对数的底。自信息的期望值就是信息论中的熵,它反映了随机变量采样时的平均不确定程度。
也就是说自信息量衡量的是信息的不确定度.
定义
单符号离散信源的数学模型用一维概率空间描述:
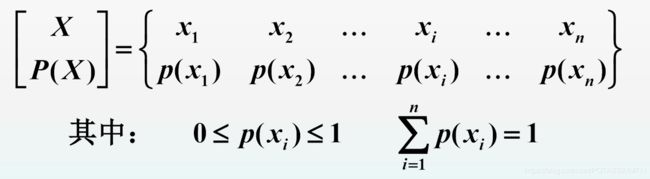
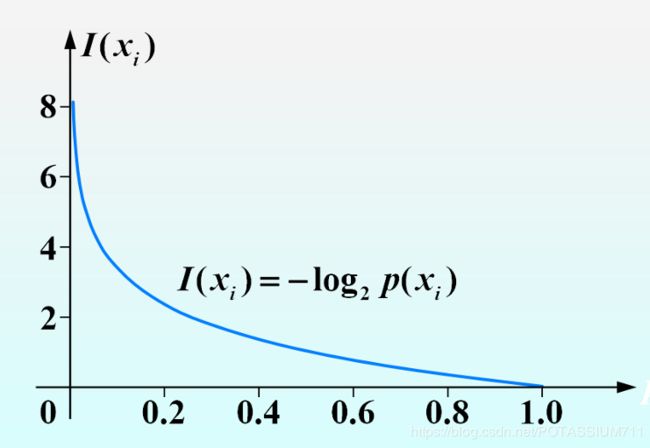
如 果 信 源 发 出 消 息 为 x i 的 概 率 为 p ( x i ) , 则 该 消 息 的 自 信 息 量 为 I ( x i ) = l o g 2 1 P ( x i ) = − l o g 2 p ( x i ) 如果信源发出消息为 x_i的概率为p(x_i),则该消息的自信息量为\\ I(x_i)=log_2\ \frac{1}{P(x_i)}=-log_2\ p(x_i) 如果信源发出消息为xi的概率为p(xi),则该消息的自信息量为I(xi)=log2 P(xi)1=−log2 p(xi)
单位为比特,即 b i t s bits bits.
含义
注意公式中的负号.
如果信宿接收到某信息,则该信息的概率为1.也就是说对于高概率的信息,接收后对于概率的改变较小.所以自信息量较小.
性质:
- 非负性
- p ( x i ) = 1 , I ( x i ) = 0 , 即 不 具 备 信 息 量 p(x_i)=1,I(x_i)=0,即不具备信息量 p(xi)=1,I(xi)=0,即不具备信息量
- p ( x i ) = 0 , I ( x i ) = + ∞ . p(x_i)=0,I(x_i)=+\infty. p(xi)=0,I(xi)=+∞.
- I ( x i ) 对 于 p ( x i ) 单 调 递 减 I(x_i)对于p(x_i)单调递减 I(xi)对于p(xi)单调递减
联合信息量
I ( x i , y i ) = − l o g 2 p ( x i , y i ) I(x_i,y_i)=-log_2\ p(x_i,y_i) I(xi,yi)=−log2 p(xi,yi)
实质上就是对于事件 x i , y i x_i,y_i xi,yi的联合发生这一事件的自信息量的考量.当X,Y独立时,
I ( x i , y i ) = − l o g 2 p ( x i , y i ) = − l o g 2 p ( x i ) − l o g 2 p ( y i , ) = I ( x i ) + I ( y i ) I(x_i,y_i)=-log_2\ p(x_i,y_i)=-log_2\ p(x_i)-log_2\ p(y_i,)=I(x_i)+I(y_i) I(xi,yi)=−log2 p(xi,yi)=−log2 p(xi)−log2 p(yi,)=I(xi)+I(yi)
也就是说当随机变量X,Y相独立时,联合信息量就是两个变量的自信息量的加和.这体现了自信息量的可加性.
条件自信息量
条件信息量衡量的是信道的转移概率,也就是前一符号已知时后一个符号的不确定度.
I ( x i ∣ y i ) = − l o g 2 p ( x i ∣ y i ) 后 验 概 率 I ( y i ∣ x i ) = − l o g 2 p ( y i ∣ x i ) 信 道 转 移 概 率 I(x_i|y_i)=-log_2\ p(x_i|y_i)\ 后验概率\\I(y_i|x_i)=-log_2\ p(y_i|x_i)\ 信道转移概率 I(xi∣yi)=−log2 p(xi∣yi) 后验概率I(yi∣xi)=−log2 p(yi∣xi) 信道转移概率
互信息量
I ( x i ; y i ) = I ( x i ) − I ( x i ∣ y i ) I(x_i;y_i)=I(x_i)-I(x_i|y_i) I(xi;yi)=I(xi)−I(xi∣yi)
互信息=先验不确定度(条件 x i d x_id xid的信息量)-后验不确定度( x i x_i xi已经确定发生下 y i y_i yi发生的概率).比如:x=下雨,y=有乌云.
互信息量的性质
I ( x i ; y i ) = I ( x i ) − I ( x i ∣ y i ) = − l o g 2 p ( x i ) + l o g 2 p ( x i ∣ y i ) = l o g 2 p ( x i ∣ y i ) p ( x i ) = l o g 2 p ( x i y i ) p ( y i ) ⋅ p ( y i ) p ( x i ) p ( y i ) = l o g 2 p ( x i y i ) p ( x i ) p ( y i ) = l o g 2 p ( y i ∣ x i ) p ( x i ) p ( x i ) p ( y i ) = l o g 2 p ( y i ∣ x i ) p ( y i ) = I ( y i ; x i ) I(x_i;y_i)=I(x_i)-I(x_i|y_i)\\ =-log_2 p(x_i)+log_2\ p(x_i|y_i)\\=log_2\ \frac{p(x_i|y_i)}{p(x_i)}\\ =log_2\frac{\frac{p(x_iy_i)}{p(y_i)}\cdot p(y_i)}{p(x_i)p(y_i)}\\=log_2\ \frac{p(x_iy_i)}{p(x_i)p(y_i)}\\=log_2\frac{p(y_i|x_i)p(x_i)}{p(x_i)p(y_i)}\\=log_2\ \frac{p(y_i|x_i)}{p(y_i)}\\=I(y_i;x_i) I(xi;yi)=I(xi)−I(xi∣yi)=−log2p(xi)+log2 p(xi∣yi)=log2 p(xi)p(xi∣yi)=log2p(xi)p(yi)p(yi)p(xiyi)⋅p(yi)=log2 p(xi)p(yi)p(xiyi)=log2p(xi)p(yi)p(yi∣xi)p(xi)=log2 p(yi)p(yi∣xi)=I(yi;xi)
- 可交换,如上面, I ( x ; y ) = I ( y ; x ) I(x;y)=I(y;x) I(x;y)=I(y;x)
- 可为正也可为负
- 独立变量之间的互信息量为0.也即 P ( x ) = P ( x ∣ y ) P(x)=P(x|y) P(x)=P(x∣y),也就是事件y发生这一条件对事件x的概率无影响.
- 互信息不大于任何一个的自信息.
Example
p ( x ) = 0.125 , p ( x ∣ y ) = 0.9 p(x)=0.125,p(x|y)=0.9 p(x)=0.125,p(x∣y)=0.9
I ( x ) = − l o g 2 ( 0.125 ) = 3 b i t s I ( x ∣ y ) = − l o g 0.9 ≈ 0.152 b i t s I ( x ; y ) = I ( y ; x ) = I ( x ) − I ( x ∣ y ) ≈ 2.848 b i t s . I(x)=-log_2(0.125)=3\ bits\\ I(x|y)=-log 0.9\approx0.152bits\\ I(x;y)=I(y;x)=I(x)-I(x|y)\approx 2.848\ bits. I(x)=−log2(0.125)=3 bitsI(x∣y)=−log0.9≈0.152bitsI(x;y)=I(y;x)=I(x)−I(x∣y)≈2.848 bits.
注意,互信息量可以为负,也就是两个信息负相关.
熵
对于整个随机变量X,其信息熵定义为x对应其信息量的数学期望,即
H ( X ) = E [ I ( x ) ] = ∑ A l l p ( x ) × − ( l o g 2 p ( x ) H(X)=E[I(x)]=\sum_{All} p(x)\times -(log_2\ p(x) H(X)=E[I(x)]=All∑p(x)×−(log2 p(x)
- 熵是非负的.
- 信源发出前表示信源的平均不确定度.
- 发出后,表示信源提供信息量的期望.
- 反映了X的随机性,即其平均携带信息量的多少.
Example
| a | b | |
|---|---|---|
| k1 | 1 | 2 |
| k2 | 2 | 3 |
| k3 | 3 | 4 |
根据定义,则有
H ( P ) = P ( a ) ⋅ ( − l o g 2 P ( a ) ) + P ( b ) ⋅ 9 − l o g 2 P ( b ) ) ≈ 0.83 H ( K ) = ∑ 1 , 2 , 3 P ( K i ) ⋅ ( − l o g 2 P ( k i ) ) H ( c ) = ∑ 1 , 2 , 3 , 4 P ( i ) ⋅ ( − l o g 2 P ( i ) ) P ( 1 ) = P ( a ) × P ( k 1 ) , . . . H( P )=P(a)\cdot (-log_2 P(a))+P(b)\cdot 9-log_2P(b))\approx 0.83\\ H(K)=\sum_{1,2,3}P(K_i)\cdot(-log_2P(k_i))\\H(c)=\sum_{1,2,3,4}P(i)\cdot(-log_2P(i))\\ P(1)=P(a)\times P(k_1),... H(P)=P(a)⋅(−log2P(a))+P(b)⋅9−log2P(b))≈0.83H(K)=1,2,3∑P(Ki)⋅(−log2P(ki))H(c)=1,2,3,4∑P(i)⋅(−log2P(i))P(1)=P(a)×P(k1),...
性质
- H ( X ) ≤ l o g 2 n , 当 且 仅 当 p i = 1 n 等 式 成 立 H(X)\leq log_2\ n,当且仅当p_i=\frac{1}{n}等式成立 H(X)≤log2 n,当且仅当pi=n1等式成立
- H ( X , Y ) ≤ H ( X ) + H ( Y ) , 当 且 仅 当 X , Y 独 立 时 等 式 成 立 . H(X,Y)\leq H(X)+H(Y),当且仅当X,Y独立时等式成立. H(X,Y)≤H(X)+H(Y),当且仅当X,Y独立时等式成立.
- H ( X , Y ) = H ( Y ) + H ( X ∣ Y ) ( 同 信 息 量 的 公 式 ) H(X,Y)=H(Y)+H(X|Y)\ \ (同信息量的公式) H(X,Y)=H(Y)+H(X∣Y) (同信息量的公式)
- H ( X ∣ Y ) ≤ H ( X ) , 当 且 仅 当 X , Y 独 立 等 式 成 立 . H(X|Y)\leq H(X),当且仅当X,Y独立等式成立. H(X∣Y)≤H(X),当且仅当X,Y独立等式成立.
Jensen不等式
假设F是区间上严格凸函数,那么
∑ i = 1 n a i f ( x i ) ≤ f ( ∑ i = 1 n a i x i ) 其 中 ∑ A l l a i = 1 当 且 仅 当 x i 相 等 时 等 号 成 立 \sum_{i=1}^na_if(x_i)\leq f(\sum_{i=1}^na_ix_i)\\ 其中\sum_{All}a_i=1\\ 当且仅当x_i相等时等号成立 i=1∑naif(xi)≤f(i=1∑naixi)其中All∑ai=1当且仅当xi相等时等号成立
二进制下的熵
联合熵
H ( X Y ) − ∑ ∑ p ( x y ) l o g 2 p ( x y ) H(XY)-\sum\sum p(xy)log_2p(xy) H(XY)−∑∑p(xy)log2p(xy)
可以推广到多个变量.
性质:
m a x [ H ( X i ) ] ≤ H ( X 1 , . . . X n ) ≤ ∑ A l l H ( X i ) max[H(X_i)]\leq H(X_1,...X_n)\leq \sum_{All} H(X_i) max[H(Xi)]≤H(X1,...Xn)≤All∑H(Xi)
也可退化到两个随机变量的情况.
条件熵
H ( X ∣ Y ) = − ∑ ∑ p ( x y ) l o g 2 p ( x ∣ y ) H(X|Y)=-\sum\sum p(xy)log_2p(x|y) H(X∣Y)=−∑∑p(xy)log2p(x∣y)
对于Y的固定值Y=y,得到X上条件概率,记作X|y,则
H ( X ∣ y ) = − ∑ A l l p ( x ∣ y ) l o g 2 p ( x ∣ y ) H(X|y)=-\sum_{All} p(x|y)log_2p(x|y) H(X∣y)=−All∑p(x∣y)log2p(x∣y)
然后对y加权平均得到结果.
平均互信息量
就是互信息量I(x;y)在联合概率空间上的期望.
I ( X ; Y ) = E [ I ( x ; y ) ] = ∑ ∑ p ( x y ) I ( x ; y ) = H ( X ) + H ( Y ) − H ( X Y ) I(X;Y)=E[I(x;y)]=\sum\sum p(xy)I(x;y)\\ = H(X)+H(Y)-H(XY) I(X;Y)=E[I(x;y)]=∑∑p(xy)I(x;y)=H(X)+H(Y)−H(XY)
- 非负性
- 对称性
- 极值: I ( X ; Y ) = I ( Y ; X ) ≤ m i n H ( X ) , H ( Y ) I(X;Y)=I(Y;X)\leq min{H(X),H(Y)} I(X;Y)=I(Y;X)≤minH(X),H(Y)
- 独立时,I(X;Y)=0
- XY一一对应时: I ( X ; Y ) = H ( X ) = H ( Y ) I(X;Y)=H(X)=H(Y) I(X;Y)=H(X)=H(Y)