机器学习 —— 李宏毅机器学习笔记(五)—— 概率生成模型
概率生成模型
概率生成模型,简称生成模型(Generative Model),是概率统计和机器学习中的一类重要模型,指一系列用于随机生成可观测数据的模型 。生成模型的应用十分广泛,可以用来不同的数据进行建模,比如图像、文本、声音等。比如图像生成,我们将图像表示为一个随机向量X,其中每一维都表示一个像素值。假设自然场景的图像都服从一个未知的分布pr(x),希望通过一些观测样本来估计其分布。也就是说,生成模型考虑的是:生成样本数据的模型是什么样的(也就是样本数据具体满足什么分布/样本会以多大的概率被生成)。
生成模型可以和贝叶斯概率公式进行结合,用于分类问题。原始贝叶斯概率公式为:
![]() ,应用到分类问题当中,可以写为如下的形式:
,应用到分类问题当中,可以写为如下的形式:
在分类问题中,训练数据中有两个类别;每个类别下有5个样本,我们想要知道新的测试样本x属于C1类别的可能性,根据贝叶斯概率公式可以得到上述图片所示的概率公式。其中,P(C1)和P(C2)表示在训练数据中,随机采样得到C1或者C2的概率,即两个类别在训练数据中所占的比重,可以计算得到。
分母项P(x)表示生成数据x的概率,此处可以由生成模型计算得到;P(x) = P(x|C1)P(C1) + P(x|C2)P(C2),因为有两个类别,每个类别下的数据具有不同的规律,服从不同的分布,都有可能生成数据x,所以相加得到生成x的概率(这里计算生成样本数据x的概率就是生成模型在做的事情)。P(C1)和P(C2)由训练数据中的统计结果可以计算得到,难点在于如何计算P(x|C1)和P(x|C2)。这里使用的方法是:极大似然估计。
极大似然估计
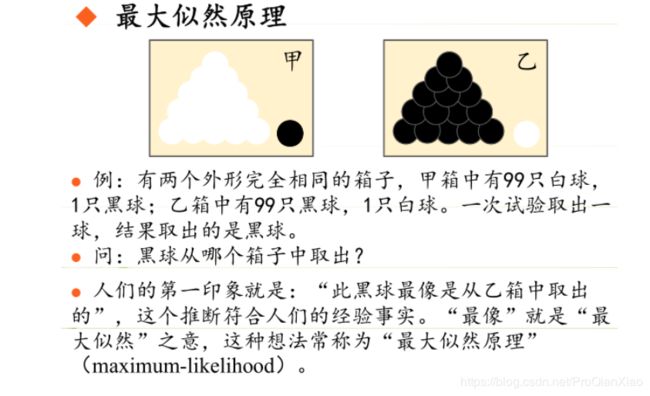
极大似然估计的原理,可以借由下面的图片进行直观的理解:
总结起来,最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
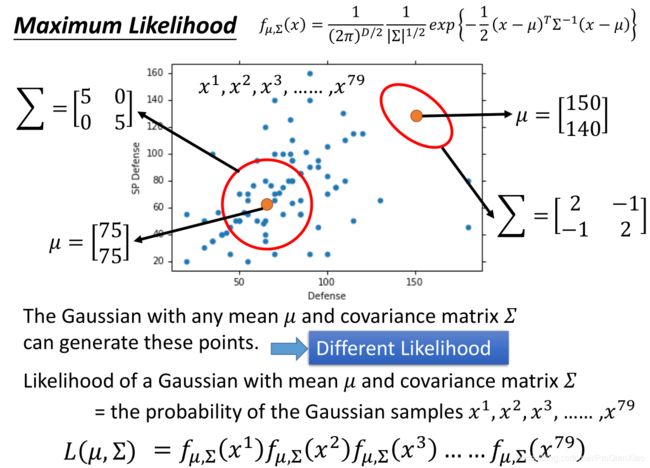
极大似然估计是建立在极大似然原理的基础上的一个统计方法。极大似然估计提供了一种给定观察数据来评估(求解)模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
总结一下:极大似然估计就是先假设生成数据(数据分布)的模型已知(比如高斯分布),但是模型的具体参数不知(不知道高斯分布中的均值和标准差),通过已有的数据,进行参数的推断求解,使得该模型(高斯分布)生成已有观测数据的可能性最大。
经过极大似然估计之后,我们可以得到每个类别下的数据满足的规律(即每个类别下的数据满足什么样的分布),那么我们就可以知道在每个类别的分布下,分别生成新的测试数据x的概率,也就是P(x|C1)和P(x|C2)。因此,我们就可以计算得到新的测试数据x属于每个类别的概率P(C1|x)和P(C2|x)。
分类问题实例
下面通过一个具体的问题情境,展示生成模型用于分类问题的过程:
预测宝可梦的类别,其中可用的特征信息如下:
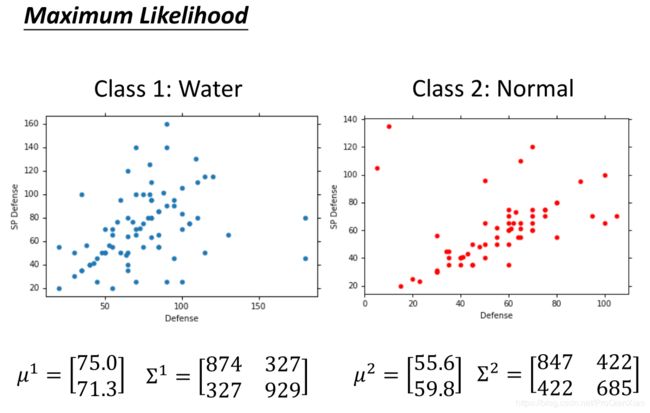
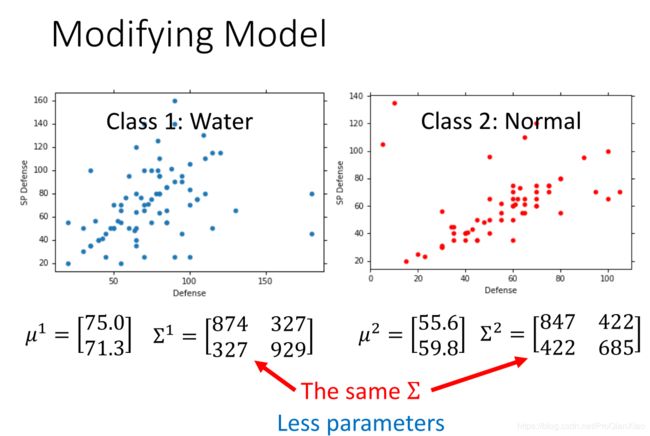
1、使用两个类别的宝可梦构成训练数据,分别是水系(Water)和正常系(Normal),数据构成如下:
2、根据贝叶斯概率公式,接下来需要计算P(x|C1)和P(x|C2),也就是分析每个类别下的数据分布规律,计算新的测试数据x分别由每个类别的数据模型生成的概率。每个宝可梦,使用其两个特征属性Defence 和 SP Defence,假设数据的分布符合高斯分布。
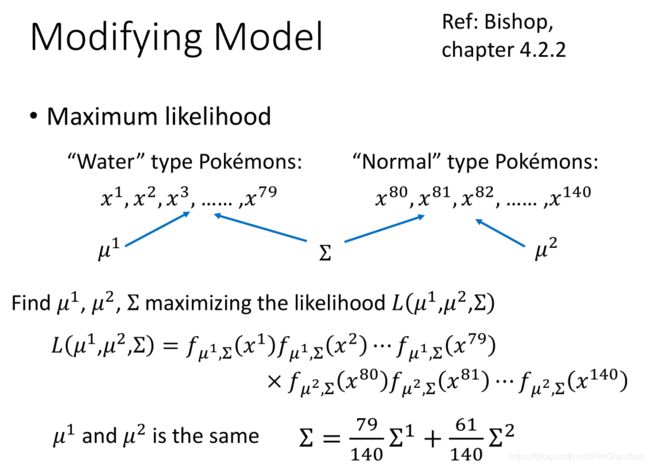
3、由极大似然估计法,计算得到高斯分布的参数(均值和标准差)。
4、经过前面的几步,接下来就可以使用贝叶斯概率公式进行分类。
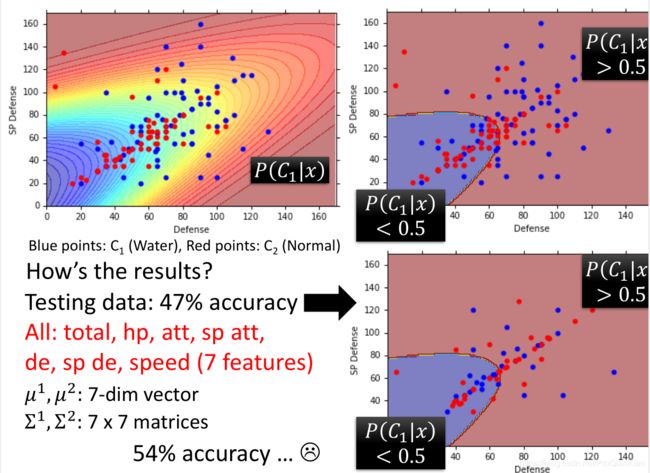
5、实验结果。
(1)测试数据上的准确率为47%,效果很差。使用更多特征(7个特征)之后,准确率为54%,提升有限。
(2)调整模型,也就是计算数据分布处的高斯分布的均值和标准差,效果有一定提升。
所以,总结一下,使用生成模型 + 贝叶斯概率分布 进行分类问题的三个步骤如下:
生成模型 + 贝叶斯概率公式的数学推导
(1) (2)
(3) (4)
(5)
经过最终的化简计算可以知道,生成模型 + 贝叶斯概率公式 本质上是寻找参数w和b的过程,如果我们直接进行参数w和b的求解,是不是就可以简化前面那么复杂的计算过程?这也是接下来要介绍的逻辑回归算法(其实判别模型都是这样做的,直接进行最终参数w和b的求解,不去考虑数据的生成)。
判别模型 VS 生成模型
两个模型最主要的区别就是:
判别模型:直接在训练数据的特征空间进行学习,对于一个输入,直接输出预测的标签。
生成模型:会考虑数据的生成情况,即每个类别下的数据分布规律,满足什么样的分布。
详细的介绍可以参加这篇博客,写得十分清楚。
参考资料
1、李宏毅机器学习-概率生成模型:https://study.163.com/course/courseLearn.htm?courseId=1208946807#/learn/text?lessonId=1278430134&courseId=1208946807
2、极大似然估计详解:https://blog.csdn.net/qq_39355550/article/details/81809467
3、判别模型和生成模型:https://blog.csdn.net/Fishmemory/article/details/51711114