matlab实现16QAM调制解调
文章目录
- 一、要求
- 二、设计
- 三、代码
- 四、结果
- 五、结论
一、要求
用基带等效的方式仿真16-QAM在AWGN信道下的误码率和误比特率性能,并与理论值相比较。
二、设计
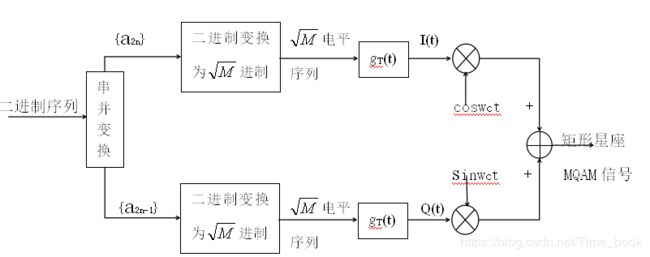
1.调制
(1)首先,一串二进制序列进入串/并变换中,进行4比特划分后再进行2比特划分成一组,按照奇数送同相路,偶数送入正交路。
(2)进入2/L电平变换,就是说二进制数变成4个十进制数,而4个十进制数是由自己的星座图设定的,即00,01,11,10分别对应于-3,-1,1,3。
(3)送入低通后滤除较小的抖动波。
(4)进入相乘器,载波cosωct与同相路波SI(t)相乘变为SI(t) cosωct, 载波cosωct经过相位移动90°与正交路波SQ(t)相乘变为-SQ(t) sinωct。
(5)两路波形经过相乘器后,进行相加,变为SI(t)cosωct- SQ(t)sinωct。
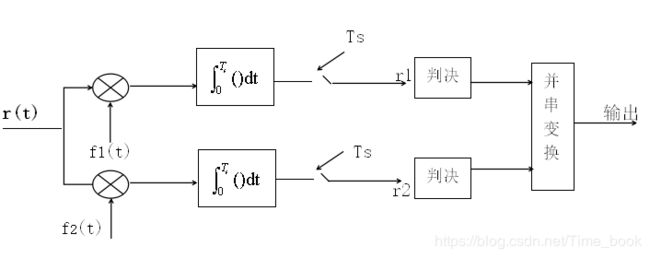
2.解调
(1)经过调制后的波形再分别与相乘器相乘,通过载波cosωct和载波cosωct经过相位移动90°后各自提取出同相分量和正交分量。
(2)进入低通形成包络波形。
(3)再进入采样判决器,选取采样点形成原始的二进制矩形波形。
(4)最后进入并/串变换,按照原先的奇偶原则形成完成的原始二进制信号。
三、代码
clear all;clc;
nsymbol= 100000;
M=16;
graycode=[0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10 ];
%graycode=[0:32]
EsN0=5:20;
snr1=10.^(EsN0/10);
msg=randi([0,M-1],1,nsymbol);
msg1=graycode(msg+1);
msgmod=qammod(msg1,M);
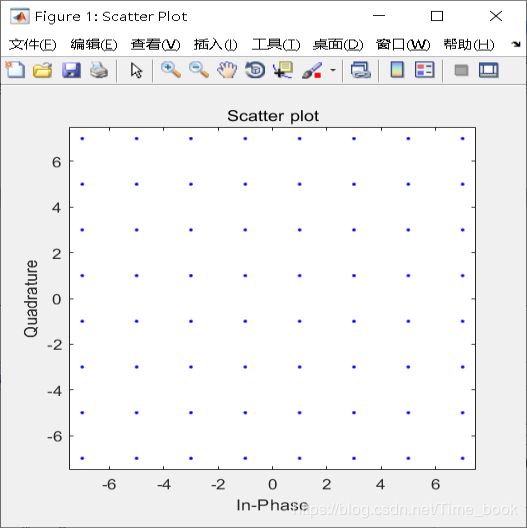
scatterplot(msgmod);
spow=norm(msgmod).^ 2/nsymbol;
for i=1:length(EsN0)
sigma=sqrt(spow/(2*snr1(i)));
rx=msgmod+sigma*(randn(1,length(msgmod))+1i*randn(1,length(msgmod)));
y=qamdemod(rx,M);
decmsg=graycode(y+1);
[err1,ber(i)]= biterr(msg,decmsg,log2(M));
[err2,ser(i)]=symerr(msg,decmsg);
end
p4=2*(1-1/sqrt(M))*qfunc(sqrt(3*snr1/(M-1)));
ser1=1-(1-p4).^2;
ber1=1/log2(M)*ser1;
figure()
semilogy(EsN0,ber,'o',EsN0,ser,'*' ,EsN0,ser1, EsN0,ber1,'-');
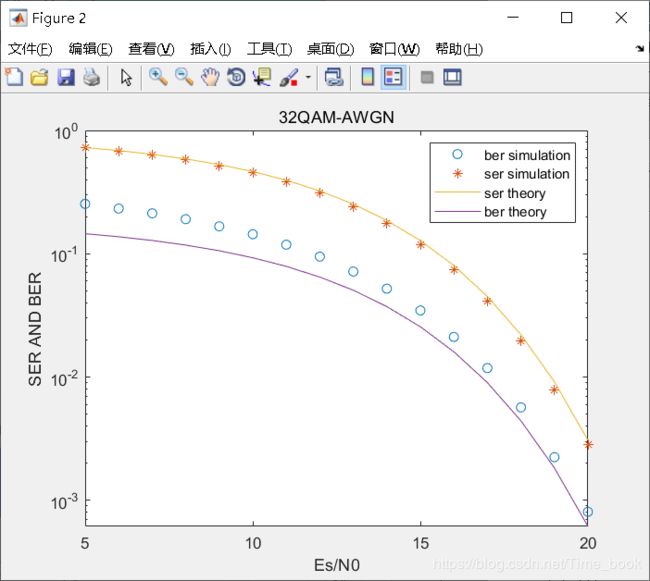
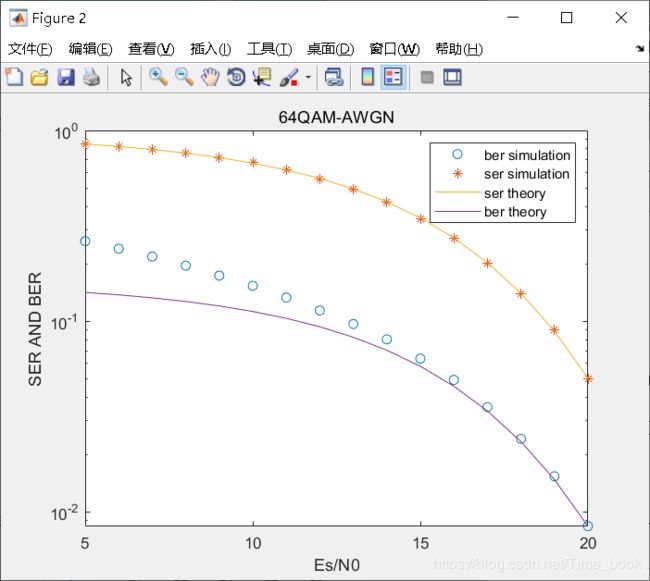
title('64QAM-AWGN')
xlabel('Es/N0');ylabel('SER AND BER');
legend('ber simulation' ,'ser simulation','ser theory' ,'ber theory');
四、结果
五、结论
由上图可知,随着信噪比的增加,误码率和误比特率越来越小。随着信噪比的增加,误比特率越来越接近理论值,而误码率几乎一直与理论值相匹配。QAM的阶数越高误码率与误比特率也就越大。而且阶数越高初始时的误比特率偏离理论值越大。