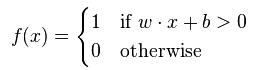一个关于Perceptron 的C++程序part1

PerceptronA basic single layer perceptron。

在看程序之前， 首先看看Perceptron的含义。

perceptron(感知器)就是一个学习一个binary classifier的算法。 实质上， 就是一个将输入的x(a real-valued vector )映射为f(x)值的函数：

NOTE： 参见深度学习1的介绍。

下面做出如下解释：

函数f(x)的值（非0即1）(根据样本的特征向量x计算函数值） ， 对样本x 进行分类。 若b 为负值， 那么输入各维特征的加权和只有大于， 才能使得我们的Perceptron计算的加权和大于0， 使得我们的样本归为正样本。改变bias b的值， 我们的decision boundary （方程为 w x + b = 0）也会发生平移改变。这是显而易见的。

但是， 如果我们的学习训练样本不是线性可分的， 那么我们的Perceptron 永远无法达到对所有的样本正确分类的时候。 因为一个线性的decision boudary(超平面) 不可能完全将一个线性不可分的（non-linear separable）样本集分开。perceptron 算法无法解决的一个典型线性不可分的问题就是异或问题。

在神经网络中， percetron 就是使用Heaviside step function 作为激活函数（activation function）。  perceptron algorithm 常常也被称作single-layer perceptron, 以便和multilayer perceptron 算法做出区别。 作为一个线性分类器， single-layer Perceptron 是最简单的feedforward neural network(前馈神经网络)。

下面我们介绍关于single-layer Perceptron的学习算法。当然， 当函数是非线性的， 而且可微的时候， 我们也可以使用dela rule 解决 single-layer perceptron.。（当然， 对于具有hidden layer 的multi-layer perceptrons, 下面的算法就不合适了。 此时必须用更加sophisticated 算法诸如BP算法。） Anyway, 这里介绍下面的一种。

在开始之前， 首先preprocessing, 定义如下变量：

•  代表对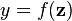于一个 input vector 输入时的输出
•  定义为bias 项， 在下面， 我们设定为0
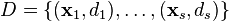• 为s个训练样本集合,其中:                                                                          (1)  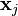为一个 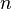-dimensional input vector

    (2)   is the desired output value of the perceptron for that input.

为了代表对应的特征， 我们如下定义：

1.  th 训练样本的输入的特征向量的第i维特征的值大小， 我们规定（即第一维特征）.
为了描述权值， 我们如下定义：

1.  是权值向量第th个权值的大小, 这个值会同特征向量的第i维特征相乘， 或者说就是第i 维特征的权重

2. 由于我们定义 , 所以权值  就隐含的代表了bias b项

为了表明权值向量,是time-dependence， 我们按照如下方式表达权值:

1.  是时刻， 权值向量第维权值的大小

2.  是 learning rate, 取值范围为： 

定义完了如上的各种变量， 下面， 我们开始学习。 具体steps 如下：

step1：对所有的weights和threshold初始化。 所有的weightes 可能被初始化为0或者某一个小的随机的值， 

     在下面的程序中， 我们选择将所有的weightes 初始化为0

step2： 对于训练集中的每一个样本  , 关于该训练样本的特征向量  和 期望的输出标记 ， 执行如下两步操作:

        2.1： 计算实际的输出：

        2.2： 按照如下方式更新权重：

                  

step3: 对于offline learning(离线学习)， 重复执行step2, 直至迭代误差函数（ iteration error 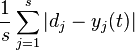）  的值小于我们指定的error

threshold ， 或者达到我们预定的迭代次数， 我们才停止继续学习。

NOTE： 对于训练样本集中的每一个样本， 该算法将updates 权重，然后作用于下一个样本， 更新权重， 一次进行下去， 直至

样本集中所有的样本作用了一遍。 而不是遍历玩所有的样本再更新权重。