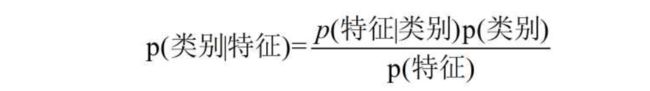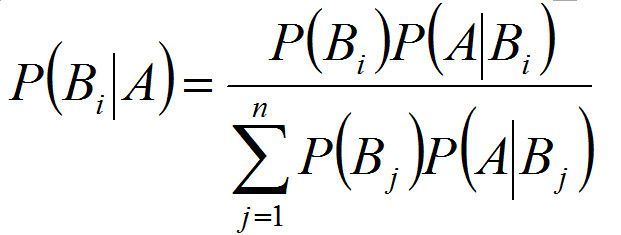我们都知道有一类他们的人生轨迹是这样的:
生物学 || 生物信息学 || 机器学习 || 人工智能
看看
知道自己在什么位置了吧?
向贝叶斯靠近的第一步就是去了解他,然后就是安装R(当然Python也完全可以胜任)。
本文R代码已经亲测有效了。
来来来,坐坐坐,听王先生讲讲贝叶斯。
分类
主要内容:
- 了解分类
- 朴素贝叶斯分类(Naïve Bayes classifier)
- ROC曲线
- 随机森林分类R实现(Random Forest)
1 分类综述
分类是逻辑的基础
资料来源
- 分类,是指按照种类、等级或性质分别归类。
根据特征判断类别
帅气?性格?上进心?身高?-----嫁(YES/NO)
体温?脸色?喉咙?咳嗽?--------感冒类型
-
数学表达
- 贝叶斯分类:以贝叶斯定理为基础
2 朴素贝叶斯
朴素 : 各特征变量之间相互独立; 贝叶斯 : 分类思想依据贝叶斯公式
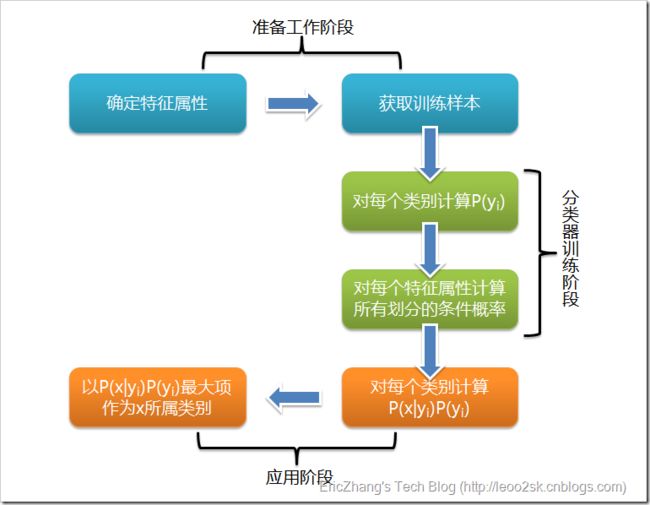
3 分类流程
-
Laplace校准
由于数据的稀疏性, 当某个类别下某个特征项划分没有出现时,就是产生这种现象,这会令分类器质量大大降低。为了解决这个问题,我们引入Laplace校准,它的思想非常简单,就是对没类别下所有划分的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为0的尴尬局面。
资料来源
.libPaths("E:/Rstudio/R_packages")
library(mlbench)
data(PimaIndiansDiabetes2)
#类变量必须是因子型变量
#数据探索和缺失值探索
data <- PimaIndiansDiabetes2
str(data)
sum(complete.cases(data))
table(data$diabetes)
prop.table(table(data$diabetes))
#数据准备
library(e1071)
ind <- sample(2,nrow(PimaIndiansDiabetes2),replace=TRUE,prob=c(0.7,0.3))
train <- data[ind == 1, ]
test <- data[ind == 2, ]
#分类器构建和应用
classifier <- naiveBayes(diabetes~., data = train, laplace=0.1)
#mean(train[train$diabetes=="neg", ]$age)
#sd(train[train$diabetes=="neg", ]$age)
pred1 <- predict(classifier, test)
pred2 <- predict(classifier, test, type = "raw")
#查看错误率
a <- table(test$diabetes, pred1)
(sum(a) - sum(diag(a)))/sum(a)
#b <- paste0(round((sum(a) - sum(diag(a)))*100/sum(a), 2), "%")
#模型评估1
library(gmodels)
CrossTable(test$diabetes, pred1, prop.r = F, prop.c=F, prop.t=T, prop.chisq = F)
#ROC曲线评估2
library(ROCR)
pred <- prediction(predictions = pred2[,2], labels = test$diabetes)
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
plot(perf,main="ROC curve", col = "blue", lwd = 3)
#ROC曲线评估3
library(pROC)
pre <- predict(classifier, test, type = "raw")
modelroc <- roc(test$diabetes, pre[,1])
plot(modelroc, print.auc = T, auc.polygon=T, grid=c(0.1,0.1),
grid.col=c("red", "red"), max.auc.polygon=T,
auc.polygon.col="skyblue", print.thres=T)
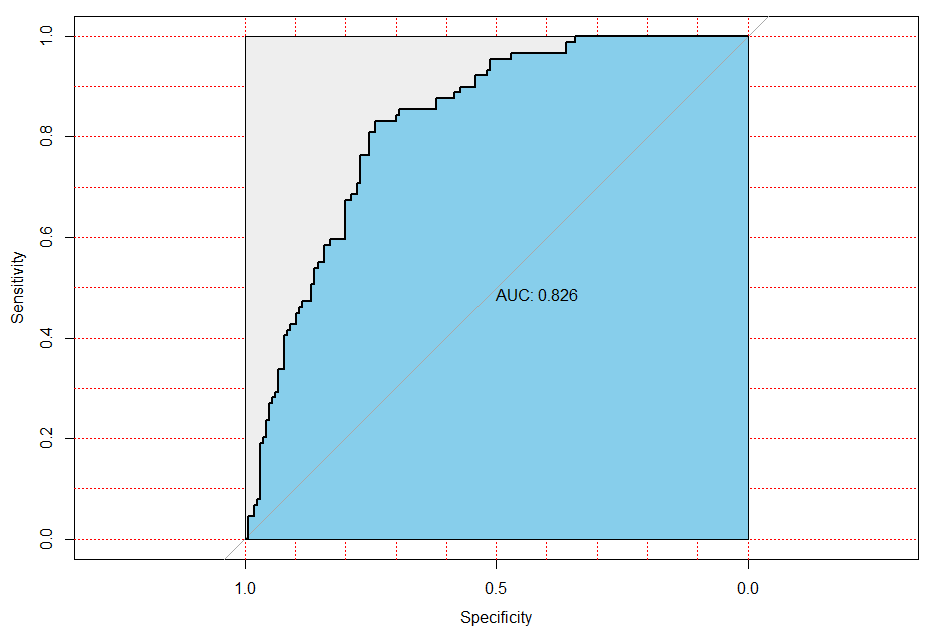
4 ROC
ROC曲线(receiver operating characteristic)是一种对于灵敏度进行描述的功能图像。ROC曲线可以通过描述真阳性率(TPR)和假阳性率(FPR)来实现。由于是通过比较两个操作特征(TPR和FPR)作为标准,ROC曲线也叫做相关操作特征曲线。
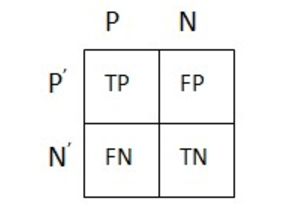
针对预测值和真实值之间的关系,我们可以将样本分为四个部分,分别是:
真正例(True Positive,TP):预测值和真实值都为1
假正例(False Positive,FP):预测值为1,真实值为0
真负例(True Negative,TN):预测值与真实值都为0
假负例(False Negative,FN):预测值为0,真实值为1
就着这个图大家在重温一下,曹先生的:假作真时真亦假,无为有处有还无
下面引入两个衡量分类的指标:
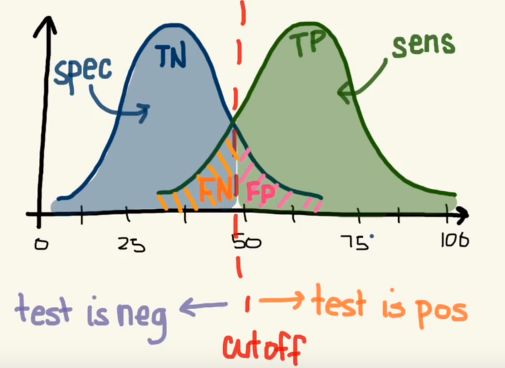
真阳性率(TPR): TPR = TP / P = TP / (TP+FN) ---------------灵敏度(sensitivity)
假阳性率(FPR): FPR = FP / N = FP / (FP + TN) -----------1-特异度(1-specificity)
不难看出,灵敏度与特异度是一张一弛,相互牵扯的。
准确度(ACC) :ACC = (TP + TN) / (P + N)
即:(猜对为阳性+猜对为阴性) / 总样本数
特征 (SPC) 或者真阴性率 :SPC = TN / N = TN / (FP + TN) = 1 - FPR
阳性预测值(PPV) :PPV = TP / (TP + FP)
阴性预测值(NPV) :NPV = TN / (TN + FN)
假发现率 (FDR) :FDR = FP / (FP + TP)
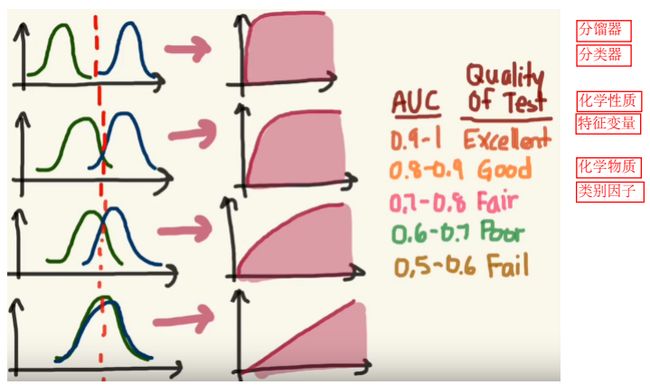
- 分类器-分馏器 类别因子-化学物质 特征变量-化学性质
5 应用
- 文本过滤:垃圾短信分类、新闻内容分类、广告分类
- 发酵异常;肠道健康;土壤类型;油田探测
6 随机森林分类
资料来源
.libPaths("E:/Rstudio/R_packages")
library(randomForest)
#数据清理:去除NA的观测样本
data1 <- data[complete.cases(data),]
str(data1)
#数据准备
ind1 <- sample(2,nrow(data1),replace=TRUE,prob=c(0.7,0.3))
train1 <- data1[ind1 == 1, ]
test1 <- data1[ind1 == 2, ]
#分类器构建和应用
rf <- randomForest(diabetes ~ ., data=train1, importance=TRUE,proximity=TRUE)
importance(rf) #变量重要性
varImpPlot(rf)
MDSplot(rf, fac=train1$diabetes, k=2)
rfpre <- predict(rf, test1, type = "prob")
#分类器评价(ROC曲线)
rfroc <- roc(test1$diabetes, rfpre[,2])
plot(rfroc, print.auc = T, auc.polygon=T, grid=c(0.1,0.1),
grid.col=c("red", "red"), max.auc.polygon=T,
auc.polygon.col="skyblue", print.thres=F)