MATLAB 层次聚类

MATLAB 的统计工具箱中的多元统计分析中提供了聚类分析的两种方法：   1.层次聚类 hierarchical clustering 2.k- means聚类

 

 

 

 

这里用最简单的实例说明 以下层次聚类原理和应用发法。

层次聚类是基于距离的聚类方法，MATLAB中通过 pdist、linkage、dendrogram、cluster等函数来完成。层次聚类的过程可以分这么几步：

(1) 确定对象（实际上就是数据集中的每个数据点）之间的相似性，实际上就是定义一个表征对象之间差异的距离，例如最简单的平面上点的聚类中，最经常使用的就是 欧几里得距离。

这在MATLAB中可以通过Y=pdist（X）实现，例如

>> X=randn(6,2)

X =

     -0.4326      1.1892

     -1.6656     -0.0376

      0.1253      0.3273

      0.2877      0.1746

     -1.1465     -0.1867

      1.1909      0.7258

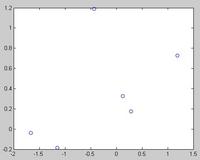
>> plot(X(:,1),X(:,2),'bo')     %给个图，将来对照聚类结果。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 图1~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

>> Y=pdist(X)

Y =

    Columns 1 through 14

      1.7394      1.0267      1.2442      1.5501      1.6883      1.8277      1.9648      0.5401    

2.9568      0.2228      1.3717      1.1377      1.4790      1.0581

    Column 15

      2.5092

例子中X数据集可以看作包含6个平面数据点，pdist之后的Y是一个行向量，15个元素分别代表 X的第1点与2-6点、第2点与3-6点,......这样的距离。那么对于M个点的数据集X，pdist之后的Y将是具有M*(M-1)/2个元素的行 向量。Y这样的显示虽然节省了内存空间，但对用户来说不是很易懂，如果需要对这些距离进行特定操作的话，也不太好索引。MATLAB中可以用 squareform把Y转换成方阵形式，方阵中位置的数值就是X中第i和第j点之间的距离，显然这个方阵应该是个对角元素为0的 对称阵。

>> squareform(Y)

ans =

           0      1.7394      1.0267      1.2442      1.5501      1.6883

      1.7394           0      1.8277      1.9648      0.5401      2.9568

      1.0267      1.8277           0      0.2228      1.3717      1.1377

      1.2442      1.9648      0.2228           0      1.4790      1.0581

      1.5501      0.5401      1.3717      1.4790           0      2.5092

      1.6883      2.9568      1.1377      1.0581      2.5092           0

这里需要注意的是，pdist可以使用多种参数，指定不同的距离算法。help pdist。

另外，当数据规模很大时，可以想象pdist产生的Y占用内存将是很吓人的，比如X有10k个数据 点，那么X占10k*8*2Bytes=160K，这看起来不算啥，但是pdist后的Y会10k*10k/2*8Bytes=400M。怕了把，所以， 废话说在前面，用MATLAB的层次聚类来处理大规模数据，大概是很不合适的。

(2) 确定好了对象间的差异度（距离）后，就可以用Z=linkage(Y)来产生层次聚类树了。

>> Z=linkage(Y)

Z =

      3.0000      4.0000      0.2228

      2.0000      5.0000      0.5401

      1.0000      7.0000      1.0267

      6.0000      9.0000      1.0581

      8.0000     10.0000      1.3717

对于M个元素的X，前面说了Y是1行M*(M-1)/2的行向量，Z则是(M-1)*3的矩阵。

Z数组的前两列是索引下标列，最后一列是距离列。例如上例中表示在产生聚类树的计算过程 中，第3和第4点先聚成一类，他们之间的距离是0.2228，以此类推。要注意的是，为了标记每一个节点，需要给新产生的聚类也安排一个标 识，MATLAB中会将新产生的聚类依次用M+1,M+2,....依次来标识。比如第3和第4点聚成的类以后就用7来标识，第2和第5点聚成的类用8来 标识，依次类推。

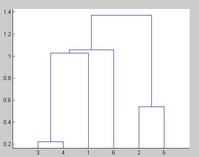
通过linkage函数计算之后，实际上二叉树式的聚类已经完成 了。Z这个数据数组不太好看，可以用dendrogram(Z)来可视化聚类树。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 图2~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

可以看到，产 生的聚类树的每一层都是一个倒置的U型（或者说是个n型，~~），纵轴高度代表了当前聚类中两个子节点之间的距离。横轴上标记出了各个数据点索引下标。

稍微注意以下的是，dendrogram默认最多画30个最底层节点，当然可是设置参数改 变这个限制，比如dendrogram(Z,0)就会把所有数据点索引下标都标出来，但对于成千上万的数据集合，这样的结果必然是图形下方非常拥挤。看你 的应用目的了，随你玩~

(3)初步的聚类树画完后，还要做很多后期工作的，包括这 样的聚类是不是可靠，是不是代表了实际的对象分化模式，对于具体的应用，应该怎样认识这个完全版的聚类树，产生具有较少分叉的可供决策参考的分类结果呢？ 这都是需要考虑的。

MATLAB中提供了cluster, clusterdata, cophenet, inconsistent等相关函数。

cluster用于剪裁完全版的聚类树，产生具有一定cutoff的可用于参考的树。

clusterdata可以认为是pdist,linkage,cluster的综合，当然更简易 一点。

cophenet和inconsistent用来计算某些系数，前者用于检 验一定算法下产生的二叉聚类树和实际情况的相符程度（就是检测二叉聚类树中各元素间的距离和pdist计算产生的实际的距离之间有多大的相关 性），inconsistent则是量化某个层次的聚类上的节点间的差异性（可用于作为cluster的剪裁标准）。