洛谷 2 月月赛 I & 加油武汉
加 油 武 汉!!!蒟蒻陈大爷
E SIR 模型 题目链接
题目描述
我们将这个模型简化一下,初始有感染者 I 人和易感者 S 人,对于每一天当前有 Ii个感染者,Si个易感者,Ri个恢复者,则每天会有 ⌈ β S i I i ⌉ \lceil \beta S_iI_i \rceil ⌈βSiIi⌉人被感染(由易感者变成感染者),有 ⌈ γ I i ⌉ \lceil \gamma I_i \rceil ⌈γIi⌉ 人被治愈(由感染者变成恢复者) 。
其中 β 为感染系数 γ为恢复系数 ⌈⌉ 为上取整符号。
求 n 天后,有多少易感者 S,感染者 I,和恢复者 R。
注: 感染者和恢复者都是每天结算的,结算的结果只和当天开始的时候的值有关,即感染者当天恢复不影响他当天感染别人。
若计算被感染人数超过易感者人数则全员被感染。
题目解析
大水题, 纯模拟, 记录特判(全员感染) 当这一次感染人数大于易感者时, 直接是为全员感染。
代码
unsigned int s, i, r;
int n;
double B, Y;
int main()
{
cin >> s >> i >> n;
cin >> B >> Y;
int total = s + i;
while(n--)
{
int ip = ceil(B * s * i);
int rp = ceil(Y * i);
//cout << ip << " " << rp << " ";
if(ip > s)
{
ip = s;
}
i += ip;
s -= ip;
r += rp;
i -= rp;
//cout << s << " " << i << " " << r << endl;
}
cout << s << " " << i << " " << r << endl;
return 0;
}
B 七步洗手法 题目链接
题目描述
给定一张含有 n 个点的无向完全图,其中 m 条边是白边,其余是黑边。
现在需要你求出同色的三元环(或者说,三角形)的个数。
题目解析
撞题了是吧(小声)QAQ~~,
先说明一下:同色三元环指的就是三条边都是相同颜色的三角形。
这道题先用容斥原理: 要求同色三角形的个数就要先求异色三角形的个数d, 然后再用所能形成的所有三角形减去d, 就是答案。
那么如何求异色三角形的个数呢。
首先发现特征: 只要有两条边颜色不同就肯定是异色三角形。
然后探究这两条边。
发现他们都连着一个共同的端点。
再去考虑这个点。
发现这个点用白边m条, 那么黑边就是n-1-m条啦, 因为完全图嘛。
所以能形成的异色三角形就是两者相乘。
考虑每一条边, 发现分别被其两个端点算了一次, 那么一共就被算了两次。
所以最后d 要除以2.
样例解释
来一波样例~~~~~~~~
5 3
1 5
2 5
3 5
图
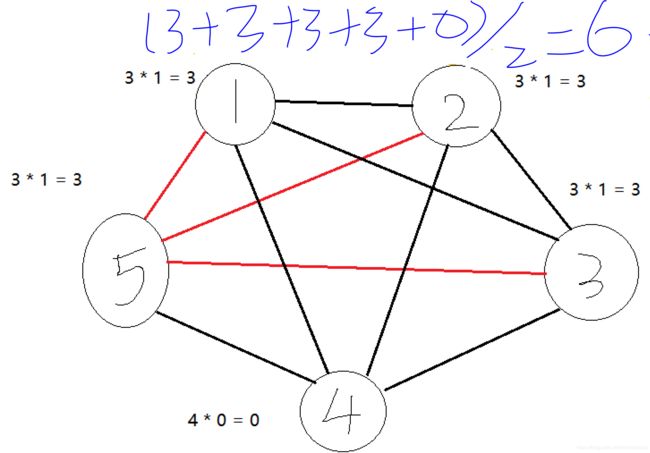
因此, 我们由图得知异色三角形数量为6, 共n * (n-1) / 2 = 10 个三角形, 10 - 6 = 4就是答案。
注释:红边表示黑边, 黑边表示白边
代码
long long n, m;
int cl[100010];
cin >> n >> m;
for(int i = 1; i <= m; i++)
{
int x, y;
cin >> x >> y;
cl[x]++;
cl[y]++;
}
long long d = 0;
for(int i = 1; i <= n; i++)
{
d += (n-1-cl[i]) * cl[i];
}
d /= 2;
cout << n * (n-1) * (n-2) / 6 - d << endl;
A 居家隔离 题目网址
题目描述
居家久了,你需要给自己找点娱乐。于是你看到这么一个游戏:
给定一个 n 元集合 { a 1 , a 2 , a 3 . . . . a n } \{a_1,a_2,a_3....a_n \} {a1,a2,a3....an},元素各不相同。
游戏总共会进行 n 轮,每轮系统会从集合中随机挑出一个元素,记作 x。你可以有如下两种选择:
取走 x,那么 x 将会是你的最终得分。
舍弃 x,此时 x,将会永久的从这个集合中删去,并且进入下一轮。
请注意,若是集合中仅剩唯一一个元素时,该元素无法被舍弃。
由于你很懒,所以你指定了一个很咸鱼的策略:
对于前 k 轮,将得到的数全部舍弃,并且记录下得到的数中的最大值,记作 y。
在第 k 轮之后,执行如下策略:
若是取得的 x > y,则直接取走 x。反之不断舍弃,直到找到了一个满足要求的 x 或是仅剩一个元素。
现在你希望知道,对于 1 到 n-1 的每一个 k,你期望下的得分是多少。
所有数请对 998244353 取模。
题目思路
首先随机这个词很重要, 代表无论哪步, 每个合法的数取到的概率都是相等的。
太难解释了, 先来看一波神犇lxn发的样例解释吧。
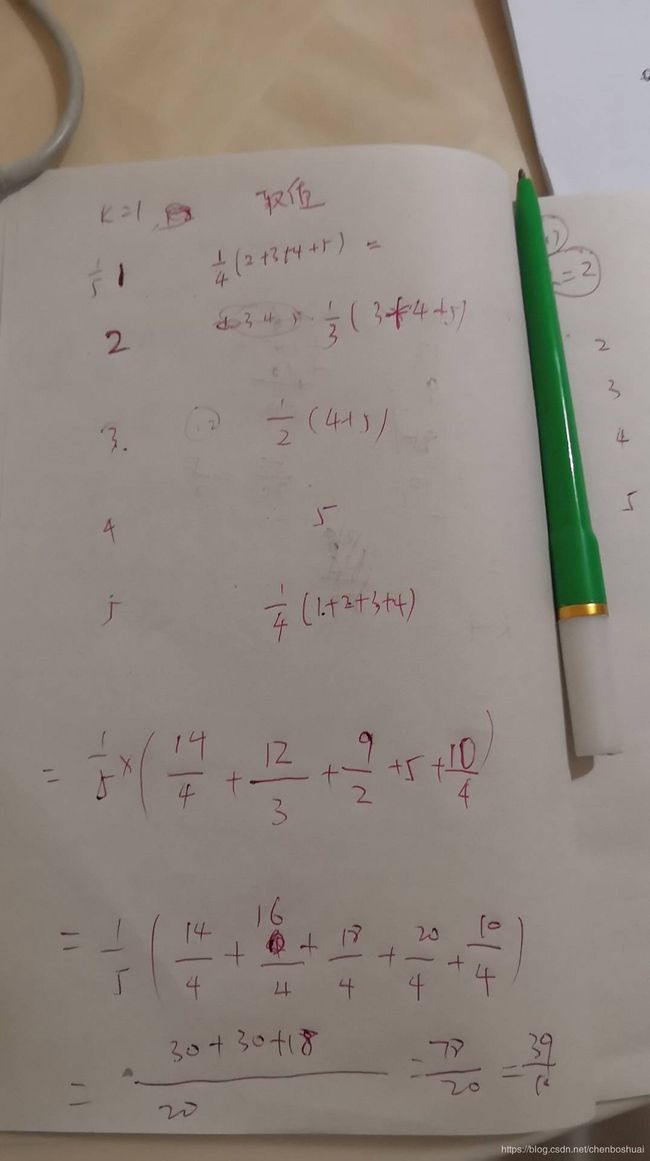
这是第一轮的情况。哦对忘发样例了。
5
1 2 3 4 5
显然对于每一轮的情况我们都有一个期望 所以答案是n-1个数(从只有一轮, 到有n-1)轮
我们来看看神犇的笔记::
首先要先选前1轮的数,那么不难想到只能选一个数。那是不是每个数都有机会选择呢。答案是:是的。所以对于这种情况每个数选择的机会就是1/5;
我们往其他方向思考, 那万一是2, 3, 4轮甚至更多时, (假如说前k轮)那么每种情况的概率是多少呢
我们可以设选出来的最大值为j, 然后去枚举最大值,而不是去枚举前k轮选出来的数的情况了, 由于机会是均等的, 最大值肯定被选, 所以就还需要从j-1个数里选k-1个数.在考虑所有情况, 就是总所有数里选k个数, 因此概率为: C j − 1 k − 1 C n k \frac{C_{j-1}^{k-1}}{C_{n}^{k}} CnkCj−1k−1再回到样例,我们可以看出选后面的数时, 只要是比前k轮最大值大的数都有可能成为最后的得分, 所以把他们的概率乘上他们的分值, 再把所有符合这样要求的数加起来, 就成为这个情况的期望, 再把所有情况的期望全加起来再除以情况数就可以得到选后面的期望, 公式: ∑ i = j + 1 n a i n − j \frac{\sum_{i = j+1}^{n} a_i}{n - j} n−j∑i=j+1nai所以一轮的期望是:: C j − 1 k − 1 C n k ⋅ ∑ i = j + 1 n a i n − j \frac{C_{j-1}^{k-1}}{C_{n}^{k}}\cdot\frac{\sum_{i = j+1}^{n} a_i}{n - j} CnkCj−1k−1⋅n−j∑i=j+1nai我们就把一个答案算出来啦!!!
当然, 注意仅剩一个元素, 代表当j = n 时我们要特判, 前面一样, 就是后面, 所有数都可能充当最后一个被舍弃的, 也就是得分的, 所以公式应该这样写。 C j − 1 k − 1 C n k ⋅ ∑ i = 1 n − 1 a i n − 1 \frac{C_{j-1}^{k-1}}{C_{n}^{k}}\cdot\frac{\sum_{i = 1}^{n-1} a_i}{n-1} CnkCj−1k−1⋅n−1∑i=1n−1ai
再考虑一下取模的问题:
我们都知道, 在模意义下除以一个数等于乘上这个数的逆元, 这里我们根据费马小定理来求逆元:
费马小定理:: a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 (mod\ p) ap−1≡1(mod p)
则可得 a ⋅ a p − 2 ≡ 1 ( m o d p ) a \cdot a^{p-2} \equiv 1(mod\ p) a⋅ap−2≡1(mod p)
则 a p − 2 a^{p-2} ap−2为a在(mod p)意义下的逆元
快速幂处理一下即可。
代码
int n;
int a[1010];
int pre[1010];
int inv_pre[1010];
int ksm(int a, int b)
{
int ans = 1;
while(b)
{
if(b & 1)
ans = 1ll * ans * a % mod;
b >>= 1;
a = 1ll * a * a % mod;
}
return ans;
}
int C(int n, int m)
{
return 1ll * pre[n] * inv_pre[m] % mod * inv_pre[n-m] % mod;
}
int sum[1010];
main:
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
}
sort(a+1, a+1+n);
pre[0] = inv_pre[0] = 1;
for(int i = 1; i <= n; i++)
{
pre[i] = 1ll * pre[i-1] * i % mod;
}
inv_pre[n] = ksm(pre[n], mod-2);
for(int i = n-1; i >= 1; i--)
{
inv_pre[i] = 1ll * inv_pre[i+1] * (i+1) % mod;
}
for(int i = n; i >= 1; i--)
{
sum[i] = sum[i+1] + a[i];
}
for(int i = 1; i <= n-1; i++)
{
int ans = 0;
for(int j = i; j <= n-1; j++)
{
ans = (ans + 1ll * C(j-1, i-1) * ksm(C(n, i), mod - 2) % mod * sum[j+1] % mod * ksm(n-j, mod - 2) % mod) % mod;
}
ans = (ans + 1ll * C(n-1, i-1) * ksm(C(n, i), mod - 2) % mod * (sum[1] - a[n]) % mod * ksm(n-1, mod-2) % mod) % mod;
cout << ans << " ";
}
cout << endl;
D 传染病研究 题目网址
题目描述
在得知 W 市爆发的肺炎之后,科学家们立刻投入了紧锣密鼓的研究之中。
(下面的部分非严谨科学,大家做题以外切勿当真)
假设某种病毒在第 x 天的传播能力为 D(x),该函数的含义为 x 的约数个数。例如 D(6)=4
现在给定你总的传播天数 n 和一个影响常数 k,你需要计算 ∑ i = 1 n D ( i k ) \sum_{i=1}^n D(i^k) ∑i=1nD(ik) 也就是 D ( 1 k ) + D ( 2 k ) + D ( 3 k ) + ⋯ + D ( n k ) D(1^k)+D(2^k)+D(3^k)+ \cdots +D(n^k) D(1k)+D(2k)+D(3k)+⋯+D(nk)
由于答案可能很大,请对 998244353 取模
题目思路
这道题实在是。。。, 好吧, 其实我也没大弄懂。。。
首先, 管他是什么, 他肯定是个数论。(肯定地说)
到现在, 也没有独立的做出来及几道数论题, 哎~~~~
先看D(i), 显而易见, 设 i = ∏ j = 1 m p j a j i = \prod_{j = 1}^{m} p_j^{a_j} i=∏j=1mpjaj, 那么根据乘法分配原理得, 每个质因子 p k p_k pk都可以选择0 ~ ak个,那么所有的质因子随机组合, 得 D ( i ) = ∏ j = 1 m ( a j + 1 ) D(i) = \prod_{j = 1}^{m} (a_j+1) D(i)=j=1∏m(aj+1)接着, 我们知道 i k = ∏ j = 1 m p j k a j i^k = \prod_{j = 1}^{m} p_j^{ka_j} ik=∏j=1mpjkaj, 所以又得 D ( i ) = ∏ j = 1 m ( k a j + 1 ) D(i) = \prod_{j = 1}^{m} (ka_j+1) D(i)=j=1∏m(kaj+1)
这样我们就把这个问题转化成了求多项式, 为什么呢,把这个式子分解一下/
 我们成功地塑造了多项式分解, 现在我们可以先把讨厌的k扔掉。先只去讨论他的系数。。。(就是那一坨a)
我们成功地塑造了多项式分解, 现在我们可以先把讨厌的k扔掉。先只去讨论他的系数。。。(就是那一坨a)
(对了, 还有一个问题, 题目让求和, 怎么办啊, 我会在下面讲解的。)
系数在这里可以用线性筛欲求。怎么求呢,
我们先来考虑一下线性筛的原理, 就是每找到一个数,就把他和比他的最小质因子还小的素数相乘并筛掉, 这样每个数都会被保证是被自己的最小质因子筛掉的
那么, 对于当前要被筛掉的数x , 他等于i * prime[j], 显而易见, 如果按照线性筛的思路的话, 她会有两种情况:
(1) i % prime[j] != 0
这种情况就相当于原来i是没有prime【j】这个因子的, 然而x却有(prime【j】性质唯一), 所以prime【j】是新增的因子, , 那么我们设i = (1+p1)(1+p2)…(1+pm)., 则x = (1+p1)(1+p2)…(1+pm)(1+pj)
这里其实都是D()的形式, 只不过省略了, 而且pj = 1因为只乘了一个prime【j】这里把prime【j】的次数看作pj,那么就是1.
但要注意一点, 以上式子里的未知数都是pi, 那么我们就不能把pj带换成1,因为以后还要注意次的关系。
注:对了, 忘了一件事, 见谅, i被拆成多项式的次数就是他的质因子个数, 上面证明过啦。
那么我们把D(X)展开就可得:(1+p1)(1+p2)…(1+pm).+pj(1+p1)(1+p2)…(1+pm)
因为pj是个未知数, 所以后面那一项都增加了一次, 得到的解析式的对应次数x的对应项的系数等于没有prime【j】的数(也就是i)的对应第x次项和第x+1次数项的系数之和。把上面的式子拆开就可证明。
(2)当i % pj == 0
pj 已经是i的因子了, 对于x来说, i转移过来没有增加新的因子, 所以pre[x] = pre[i], 最后同上面一样加以计算。
来说以下代码里的形式, pre不说了, 设b【i】【j】表示i这个数按上述规则拆成多项式后第j次方项对应系数。
最后其实要把b数组变成前缀和的形式, 因为最后答案要求和吗
最后再乘k, 用秦久韶公式就好了吗QAQ
代码
//copy form lyp
#includeF 体温调查 题目网址
题目描述
给出一颗树,根结点编号为
1。有一名医护人员从根出发,沿着树边移动,去每个叶子采集信息,最后返回根。他的采集顺序是固定的,每当走到一个结点
u,他会先走向编号最小的孩子,并访问完其中所有的家庭并回到
u,然后再走向编号第二小的孩子,依此直到访问完u子树中所有的家庭返回上一层。可以发现访问叶子的顺序也正好是家庭住址列表上的顺序。
沿着树边移动需要一定时间,为了节约时间,可以将家庭列表分成连续的
k段,并让k个医护人员同时从根出发,每人访问一个区间中的家庭然后返回。请你计算出统计完所有家庭的体温所需要的最短时间
题目思路
erfen(二分)!!!!
求最大时间最小值, 一看就是二分, 检查在最大时间内,遍历完所有叶节点的人数, 如果大于要求的, 那么就往大了分, 反之, 就往小了分。
然后, 现在是想如何算距离, 发现只是相邻叶结点的距离(题目中的节点是按顺序给出的)可以用LCA来求, 如图:
这幅图中, 设disi表示i节点到根的距离, 那么ll和lr之间的距离就为dislr + disll - 2 * dislca;
代码中因为是一个一个叶节点添加, 一个一个判断, 所以用dis叶节点, 减去dislca即可。
还有求lca时其实这题可以不用倍增或者说是tarjan,可以用dfs, 回溯时改编子树的同时深度最浅的那个节点就是lca了!!!
代码
//二分答案,枚举距离检查。
//记录每个叶子节点最近的前一个叶子节点。,求每个节点与其相邻的叶子
#include小结
最近的2020开头虽然不好, 但我还是要感谢我身边支持我的同学, 老师, 父母, 新的一年, 一起努力, 同时也为武汉加油, 中国最棒!!!!