NOI Online #2入门组
NOI Online #2入门组
A 未了
题目描述
由于触犯天神,Sisyphus 将要接受惩罚。
宙斯命令Sisyphus推一块儿巨石上长度为L的山坡。Sisyphus匀速向上推的速度为每年v的长度(由于是匀速, 故经过1/2年将能向上推v/2的长度)。然而, 宙斯并不希望Sisyphus太快到达山顶。宙斯可以施展n个魔法, 若他施展第i个魔法, 那么Sisphus第一次到达位置ai时, 他将会同巨石一起滚落山底, 并从头推起。(滚落的时间忽略不计, 即可看做第一次到达位置ai后, Sisyphus立即从山地重新出发)
现在, 宙斯有q个询问。每个询问ti, 他want to know, 他最少需要实战多少个魔法才能使Sisphus到达山顶所用的年数大于ti。
题目思路
根据题目描述, 使用第i个魔法相当于多走了a[i]的路, 路越长, 时间越长, 所以根据贪心思想, 因为要求最少使用的魔法数量, 假设长度不变, 那么取得魔法增加的路程越长, 数量就越少, 根据这个, 我们可以排序, 然后算出前i个魔法使用后的时间,(排好序后, 取前i个一定是最优方案)。
下面, 就是取多少个的问题了。
显然, 数列满足单调性(因为排序了呗), 二分即可。
详细内容见代码
代码
double L, v;
double a[N];
double b[N];
long long a;
//b[i] 表示使用前i个魔法后爬上山顶所用的时间
bool cmp(int a, int b)
{return a > b;}
int main()
{
cin >> n >> L >> v;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
}
sort(a+1, a+n+1, cmp);//魔法长度从大到小排序:贪心
b[0] = L / v//t = s / v, 小学内容。。。
for(int i = 1; i <= n; i++)
{
b[i] = a[i] / v + b[i-1];//把每一块多走得时间给我加上
}
int q;
cin >> q;
while(q--)//对于每一个询问
{
double t, ans;
cin >> t;
if(b[mid] <= t)
{
printf("-1\n");
return 0;
}//如果所有魔法都使用了但爬上山顶的时间还是小于t的话, 无解, 输出-1
//下面是二分。。。
int l = 0; r = n, ans = 0;
while(l <= r)
{
int mid = (l+r) >> 1;
if(b[mid] > t)//使用前mid个魔法所用的时间超过t的话
{
ans = mid;
r = mid-1;
}
else
{
l = mid + 1;
}
}
printf("%d\n", ans);
}
return 0;
}//完结撒花。。。
呵呵, 其实后面都没有这么详细的代码了。。。
B 荆轲刺秦王
题目描述
咸阳宫的地图可以描述为一个n行m列的矩形。 在这里, 我们规定每一行从左到右为x轴正方向, 每一列中从上到下y轴为正方向,左下角点的坐标为(1,1)。矩形中的点可以分为4种:
1.起点, 也就是荆轲所在点, 在地图中用字符’s’代表。
2.终点, 也就是嬴政所在点, 在地图中用字符’T’代表。
3.卫兵, 再地图中用一个正整数 a i , j a_{i,j} ai,j代表。 在这里,, 一个卫兵 ( i , j ) (i,j) (i,j)可以观察到与他曼哈顿距离小于 a i , j a_{i,j} ai,j的点, 也就是卫兵 ( i , j ) (i,j) (i,j)可以观察到所有满足 ∣x−i∣+∣y−j∣< a i , j ai,j ai,j的点 ( x , y ) (x,y) (x,y)。
4.空地, 在地图中用字符’.'代表,
荆轲的正常移动方式为每秒向八连通的任意方向前进一格。如下图, 中间的点为荆轲当前所在点。每一秒, 他可以走向其余的八个点。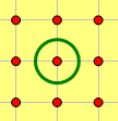
需要注意的是,正常移动时, 荆轲不能踏进任何一个有卫兵或者卫兵能观察到的格子。当然, 他也不能走出咸阳宫, 也就是说, 无论何时, 荆轲的坐标(x,y)都必须满足 1 ≤ x ≤ m 1 \leq x \leq m 1≤x≤m且 1 ≤ y ≤ n 1 \leq y \leq n 1≤y≤n
荆轲还有两种技能:隐身和瞬移。
1.隐身:下一秒荆轲进入隐身状态,卫兵观察不到荆轲, 荆轲可以进入卫兵的观察范围内, 但仍然不能进入卫兵所在的格子。注意这个状态只能持续一秒
2.瞬移:荆轲下一秒移动的距离改为d, 但这时只能向上下左右四个方向移动
即可以移动到 ( x + d , y ) , ( x − d , y ) , ( x , y + d ) , ( x , y − d ) (x+d, y), (x-d, y), (x, y+d), (x, y-d) (x+d,y),(x−d,y),(x,y+d),(x,y−d).在本题中, 两种技能同时使用, 而且不考虑冷却时间, 即一次用完可以立即用下一次, 两种技能都分别有使用次数限制, 你也可以不用完所有次数。
现在给出咸阳城的地图,请计算荆轲到达秦王所在点所需的最短时间。此外,在所用时间相同情况下,荆轲希望使用的两种技能总次数尽可能少;在所用时间与技能次数相同情况下,荆轲希望使用的隐身次数尽可能少。
题目描述
我跪了。。。。。。。。。。。。。。。。。。。。。
一看就是搜索(对, 搜索, 做完后再也不想学搜索)
广搜显然是靠谱的。
状态肯定有坐标, 当前走的步数,瞬移和隐身。
结构大约是这样的:
可能大家还有点懵, 或者说完全懵, 那么看代码吧。。。。细节在里面。
代码
struct Point
{
int step;//从起点到当前点走了多少步
int x;//横坐标
int y;//纵坐标
int tl;//已经用的瞬移次数
int inv;//已经用的隐身次数
Point(){}
Point(int a, int b, int c ,int d, int e)
{
step = a;
x = b;
y = c;
inv = d;
tl = e;
}//构造函数
};
Point ans = {0x3f3f3f3f, 0, 0, 0x3f3f3f3f, 0x3f3f3f3f};//答案
int n, m, c1, c2, d;
int map[310][310];//地图
int sx, sy, ex, ey;//终起点坐标
int vis[310][310][310][310]//vis[i][j][k][l]对应x, y, inv, tl;
int bl[310][310];//被看到次数的差分数组;
void lookaround(int x, int y, int k)//卫兵所处位置(x,y)和他的值
{
//分别处理横坐标与纵坐标的区间, 左+, 右减。
//枚举到(x, y) 点的距离
for(int i=0;i<=k;i++){
bl[max(x-i,1)][max(y-(k-i),1)]++;
bl[max(x-i,1)][min(y+(k-i),m)+1]--;
bl[min(x+i,n)][max(y-(k-i),1)]++;
bl[min(x+i,n)][min(y+(k-i),m)+1]--;
}//max, min是为了防止越界。
}
bool islook[310][310];//当前格子是否能被卫兵看见
void solve()
{
for(int i=1;i<=n;i++){
int sum=0;
for(int j=1;j<=m;j++){
sum+=bl[i][j]; //求出islook数组(前缀和)
if(sum>0)islook[i][j]=1;//有卫兵能看到这儿
}
}
}
queue<Point> q;
Point better(Point a, Point b)
{
/*请计算荆轲到达秦王所在点所需的最短时间。此外,在所用时间相同情况下,荆轲希望使用的两种技能总次数尽可能少;在所用时间与技能次数相同情况下,荆轲希望使用的隐身次数尽可能少。*/
//根据这个, 可以翻译出这样一段代码
if(a.step != b.step)
{
return a.s < b.s? a : b;
}
if(a.tl + a.inv != b.tl + b.inv)
{
return a.tl + a.inv < b.tl + b.inv ? a : b;
}
return a.inv < b.inv ? a : b;
}
const int dx[8]={1,0,-1,0,1,-1,-1,1},dy[8]={0,1,0,-1,1,1,-1,-1};//坐标变化量, bfs里用循环枚举下一步位置。
void bfs()
{
while(!q.empty())
{
Point now = q.front();
q.pop();
if(q.step > ans.step)
{
continue;//如果当前状态的步数已经比答案步数要大, 没有必要搜索下去了,因为你后来肯定还要走。
}
if(now.x == ex && now.y == ey)//如果当前状态已经走到终点了
{
ans = better(ans,now);//答案去两者更好的那一个。
continue;
}
for(int i = 0; i < 8; i++)//不瞬移, 八连通
{
int nx = now.x + dx[i];
int ny = now.y + dy[i];//下一步做标
if(nx<1||nx>n||ny<1||ny>m||map[nx][ny]>0)continue;//越界和有卫兵在那站着的格子都不能走到
if(islook[nx][ny])//被卫兵看到, 要用隐身
{
if(vis[nx][ny][now.inv+1][now.tl]||now.inv+1>c1)continue;//隐身次数超过上限或当前状态已经在队列了
vis[nx][ny][now.inv+1][now.tl] = 1;
q.push((Point){s+1,nx, ny, now.inv+1, now.tl});
}
else//不隐身
{
if(vis[nx][ny][now.inv][now.tl])
{
continue;
}
vis[nx][ny][now.inv][now.tl] = 1;
q.push((Point){s+1,nx, ny, now.inv, now,tl});
}
}
for(int i = 0; i < 4; i++)//瞬移, 只能走上下左右四个方向
{
int nx = now.x + dx[i]*d;
int ny = now.y + dy[i]*d;//一次能走d格
if(nx<1||nx>n||ny<1||ny>m||map[nx][ny]>0)continue;
if(islook[nx][ny])//还要用隐身
{
if(vis[nx][ny][now.inv+1][now.tl+1]||now.inv+1>c1 || now.tl+1>c2)
{continue;}
vis[nx][ny][now.inv+1][now.tl+1] = 1;
q.push((Point){s+1,nx, ny , now.inv+1, now.tl+1});
}
else//不用隐身
{
if(vis[nx][ny][now.inv][now.tl+1]||now.tl+1 > c2)
{
continue;
}
vis[nx][ny][now.inv][now.tl+1] = 1;
q.push((Point){s+1, nx, ny, now.inv, now.tl+1});
}
}
}
int main()
{
cin >> n >> m >> c1 >> c2 >> d;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
string s;
cin >> s;//输入;
if(s == 'S')//是起点, 对应-1(这是自己想的对应关系, 下面也是
{
sx = i;
sy = j;
map[sx][sy] = -1;
q.push((Point){0, sx, sy, 0, 0});//bfs第一个状态.
vis[sx][sy][0][0] = 1;//此状态在队列里.
}
else if(s == 'T')//终点对应-2;
{
ex = i;
ey = j;
map[ex][ey] = -2;
}
//空地为0;
else//卫兵。
{
int x=0;
for(int i=0;i<s.size();i++)
x=(x<<1)+(x<<3)+(s[i]^'0');//类似快读。
map[i][j] = x;//他站的位置
lookaround(i, j, x-1);//他看到的位置。
}
}
}
solve();//求出每个格子是否被卫兵看到
bfs();//广搜
if(ans.step = 0x3f3f3f3f)//没被更新过
{
printf("-1\n");
}
else
{
printf("%d %d %d\n", ans.step, ans.inv, ans.tl);
}
return 0;
}
体会到了吐血的感觉qwq
C 建设城市
题目描述
球球是一位建筑师。一天, 他收到市长的任务:建设城市。球球打算建造2n座高楼。为了保证城市美观, 球球做出了如下计划:
1.球球喜欢整齐的事物, 他希望高楼从左到右排成一行, 编号依次为1~2n。
2.他喜欢整数, 他要求每座高楼的高度都是正整数。
3.由于材料限制, 高楼的高度无法超过m。
4.球球喜欢中间高两边低的造型, 他要求前n座楼高度不下降, 后n座楼高度不上升。
5.球球打算选两座编号为x,y的高楼作为这座城市的地标, 他认为只有当这两座高楼高度相等时, 才会让城市变得美观。
球球把自己的想法告诉了市长。市长希望得知所有建设城市的方案数。两种方案不同,当且仅当某座高楼的高度在两个方案中不同。这个问题可难倒了球球。球球找到了你,希望你能帮他算出答案。由于答案可能很大,你只需要给出答案对998244353 取模后的结果。
题目思路。
首先, 因为x和y相等, 而且这个数列最值肯定是n(由4推出)。所以我们可以分情况讨论。
1.(x <= n < y)
枚举x, y高度, 设当前为h。则:
1~x-1的取值范围是[1,h]。
x+1~n的取值范围是[h, m];
n+1~y的取值范围是[h,m];
y+1~2n的取值范围是[1,h];
可见, 我们只要求出每一块的方案数, 再根据分步乘法计数原理全乘起来就是最后的答案啦。
那么怎么求呢。
假设当前有a个数, 取值范围里有b个数, 那么方案数是。。。
看这儿!!
由此可以得到每块儿答案为 C a + b − 1 b − 1 C_{a+b-1} ^ {b-1} Ca+b−1b−1
2. (x, y 在n同侧)
将(x, y)中间那部分看成一个高楼, 那么可见答案就为 C n + m − 1 m − 1 × C n + m + x − y − 1 m − 1 C_{n+m-1}^{m-1} \times C_{n+m+x-y-1} ^{m-1} Cn+m−1m−1×Cn+m+x−y−1m−1
最后取模和逆元, 你懂的。。。
代码
#include