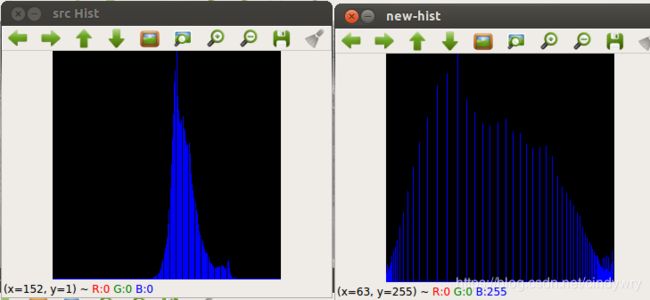
直方图修改技术进行图像增强

灰度级的直方图描述了一幅图像的基本概貌，用修改直方图的方法增强图像是实用而且有效的方法之一。
直方图的定义：
灰度级的直方图是什么？
就是反映一幅图上灰度级与出现这种灰度的概率之间的关系。如直角坐标系中，横坐标表示一幅图灰度的等级（灰度级），纵坐标表示某个特定等级的灰度在该幅图像上出现的次数（概率）。假设某个图片的灰度级r的范围为0到1（r=0表示黑，r=1表示白），某个灰度出现的概率为Pr(r),如果灰度的取值是连续的话，那么其对应的概率Pr(r)也连续，可称Pr(r)为概率密度函数这样可针对一幅图像在这个坐标系中作出一幅图像出来，如下所示：
                                          
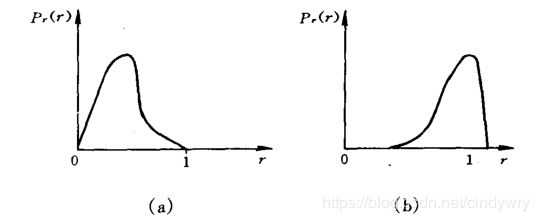
                                                                                          图像灰度概率密度函数曲线图
从图像的灰度级分布可看出一幅图的灰度分布特征，（a）中可看出大多像素点分布在较暗区域，所以这幅图肯定比较暗，而（b）则正好相反，改图一定是相对较亮。在数字图像处理中引入离散形式，离散形式下以上图像可表现为如下图：
                                

                                                                                    离散情况下的灰度级分布
rk为离散灰度级，Pk(rk)为某个灰度级出现的密度，可有如下式表示：
                                                                       

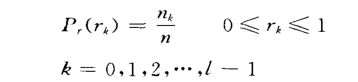
 直方图修改技术的基础
直方图修改技术的目的就是：通过改变一张图片的灰度级的分布来增强图像的清晰度。说白了就是找到一种映射关系使得这张图片的灰度级分布尽量均匀，或者说尽量使得每个灰度级的像素数量相等，从而达到图像清晰化的效果，如下图所示： 
                             
                                                修改前                         修改后                                           理想修改后直方图
                                                                                                                                                                                                                     
找到一种映射关系
假设有一种关系如下；


s是r的映射，在s域中s对应的灰度级密度函数为Pr(s)，在该映射中由概率可知，如果已知随机变量ξ的概率密度为Pr(r),而随机变量η是ξ的函数，即η=Τ(ξ)，η的概率密度为Ps(s),则可由Pr(r)求出Ps(s)，s与r有着如下单调关系：
                             

                                               一种 灰度变换关系                                                          s与r的变换关系

    
                   
 对上式两边求导可得到随机变量η的分布密度函数Ps(s)为：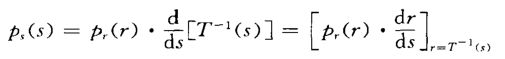

由如上图可知，通过变换函数T(r)可改变图像灰度级的概率分布函数，从而改变图像的灰度级层次，这就是直方图修改技术的基础。
直方图均衡化处理
直方图均衡化处理的映射关系关系为如下，即：以积累分布函数变换法为基础。

以上这种映射关系可使得一张图像的灰度级分布均匀化，
有如下推到可证明： 
对该映射两边求导得：

 把上式带入求Ps(s)的函数

可得：

由上式的推到可见，在变换后的变量s的定义域内的概率密度是均匀分布的。由此可见，用r的累积分布函数作为变换函数可产生一幅灰度级分布具有均匀概率密度的图像。其结果扩展了像素取值的动态范围。 
实例：

void calcHist(const Mat* images, 
    int nimages, 
    const int* channels, 
    InputArray mask, 
    SparseMat& hist, 
    int dims, 
    const int* histSize, 
    const float** ranges, 
    bool uniform=true, 
    bool accumulate=false )

关于第一个函数原型的详细参数如下：
constMat* images：为输入图像的指针

int nimages：要计算直方图的图像的个数。此函数可以为多图像求直方图，我们通常情况下都只作用于单一图像，所以通常nimages=1

const int* channels：图像的通道，它是一个数组，如果是灰度图像则channels[1]={0};如果是彩色图像则channels[3]={0,1,2}；如果是只是求彩色图像第2个通道的直方图，则channels[1]={1}

IuputArraymask：是一个遮罩图像用于确定哪些点参与计算，实际应用中是个很好的参数，默认情况我们都设置为一个空图像，即：Mat()。

OutArrayhist：计算得到的直方图int dims：得到的直方图的维数，灰度图像为1维，彩色图像为3维

const int* histSize：直方图横坐标的区间数。如果是10，则它会横坐标分为10份，然后统计每个区间的像素点总和constfloat** ranges：这是一个二维数组，用来指出每个区间的范围后面两个参数都有默认值，uniform参数表明直方图是否等距，最后一个参数与多图像下直方图的显示与存储有关
 

#include "opencv2/highgui/highgui.hpp"  
#include "opencv2/imgproc/imgproc.hpp"  
#include   
#include   
  
using namespace std;  
using namespace cv;  
// 得到图像的直方图
 MatND getHistogram(Mat &image)    
{  
    MatND hist;//输出的结果存储的 空间 ，用MatND类型来存储结果  
    int channels[] = {0}; //需要计算图像的哪个通道（bgr空间需要确定计算 b或g或r空间）  
    int dims = 1;  
    int histSize[] = {256};///直方图的每一个维度的 柱条的数目（就是将灰度级分组）     
    float granges[] = {0, 255};  //定义一个变量用来存储 单个维度 的数值的取值范围  
    const float *ranges[] = {granges}; //确定每个维度的取值范围，就是横坐标的总数    
    calcHist(&image, 1, channels, Mat(), hist, dims, histSize, ranges);  
    return hist;  
}  
 //  将图像直方图展示出来  
 Mat getHistogramImage(Mat &image) 
{  
    MatND hist = getHistogram(image);  
    Mat showImage(256, 256, CV_8UC3, Scalar(0));  
    int i;  
    double maxValue = 0;  

	//任何一个图像的某个像素的总个数有可能会很多，甚至超出所定义的图像的尺寸，
    //所以需要先对个数进行范围的限制，用minMaxLoc函数来得到计算直方图后的像素的最大个数  
    minMaxLoc(hist, 0, &maxValue, 0, 0);

	//将像素的个数整合到图像的最大范围内
    for(i = 0; i < 256; i++)  
    {  
        float value = hist.at(i);  
        int intensity = saturate_cast(256 - 256* (value/maxValue));  
        rectangle(showImage, Point(i,256 - 1), Point((i+1)-1, intensity), Scalar(255));  
    }  
    return showImage;  
}
 //主函数
 int main()  
{  
    Mat image = imread("h.png");  
    if(!image.data)  
    {  
        cout << "fail to load the image" << endl;  
        return 0;  
    }  
    Mat HistogramImage = getHistogramImage(image);  
    namedWindow("src-Image");  
    imshow("src-Image", image); 
	//源直方图
    namedWindow("src Hist");  
    imshow("src Hist", HistogramImage); 

	Mat Hist,gray; 
	cvtColor( image, gray, CV_BGR2GRAY );  //rgb类型转换为灰度类型
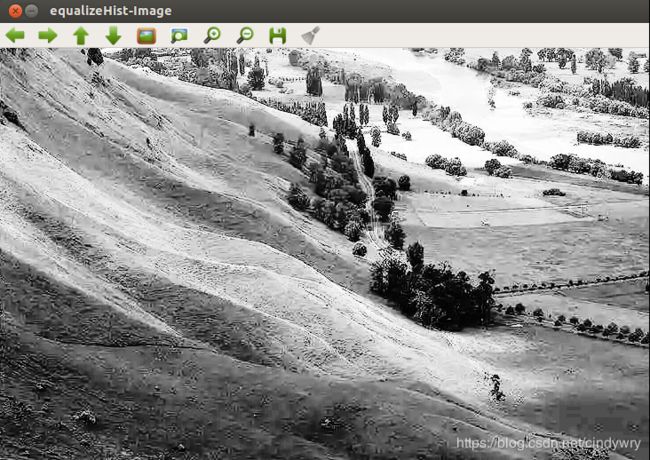
	equalizeHist(gray, Hist);   //直方图均衡化

	namedWindow("equalizeHist-Image");
	imshow("equalizeHist-Image", Hist);
	
	Mat HistImage = getHistogramImage(Hist);
	namedWindow("new-hist");
	imshow("new-hist", HistImage);
	waitKey(0);  
    return 0;  
} 

https://blog.csdn.net/u011574296/article/details/70880423