【纪中2020.2.5日】模拟赛题解

目录

T1：最大值
T2：火柴
T3：游戏
T4：hack的比赛

又是一届异常快乐的%你赛……

回归正题…T1：最大值

题目描述

给定n个数，｛x1,x2,…,xn｝要求从中选出至少一个数，至多n个数，使得乘积之和最大。

输入

第一行整数n，表示有多少个数
接下来n行，每行一个整数xi,-10 ≤xi≤ 10

输出

输出一行，表示最大乘积

样例输入

Sample Input1:

3
-1
2
-4

Sample Input2:

3
3
2
-4

分析：枚举

记录下最大的负数(用来除)，0的个数(判断结果)。
注意一些细节问题，
再做一波判断就好了。
——————————————————————————————

CODE：

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
int x,w,k,n,i,maxx=-0x7fffffff+1;//int最小值
int ans=1;//为1，不然怎么乘都是0
int main(){
	freopen("max.in","r",stdin);
    freopen("max.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>x;
		if(x!=0) ans*=x; //先乘起来
		else w++;  //是0就计数
		if(x<0)
		{
			if(maxx<x) maxx=x;  //找最大负数
		}
	}
	if(ans<0&&ans!=maxx) ans/=maxx;  //除
	if(w==n) cout<<0;  //全部是0
	else cout<<ans;

return 0;
}

T2：火柴

题目描述

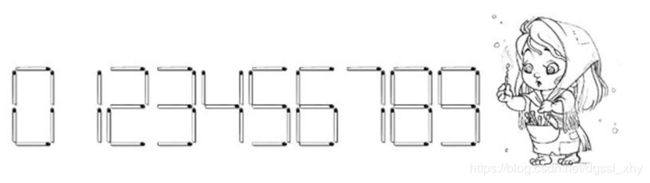
给定一个N位的数，将火柴棍重新排列后，能得到的最大的数是多少？
注意不能多出或者少一位, 火柴棍要全部用上.

输入

第一行整数T，表示数据组数
接下来T行，每行一个整数N， 然后是N位数，表示原来的数，可能会有前导0，中间用空格隔开。

输出

对于每组数据，输出一行，最大的能得到的数是多少。

样例输入

3
1 3
3 512
3 079

样例输出

5
977
997

分析：贪心

记录下每个数字需要的火柴数(图片给你了)，从高位到低位，从大到小枚举，如果摆了这个数字后，后面全放8或全放2行不行(要注意：要恰好用完）。输入为字符，注意转换一下。
——————————————————————————————

CODE:

#include 
#include 
using namespace std;
const int cnt[10] = {6,2,5,5,4,5,6,3,7,6};  //火柴棒数
int t,n,sum,cur;
char ch;
inline bool judge(int i,int j)
{return i * 2 <= j && j <= i * 7;}  //判断函数
int main()
{
	freopen("match.in","r",stdin);
	freopen("match.out","w",stdout);
	scanf("%d",&t);
	while(t--)
	{
		sum = 0;
		scanf("%d",&n);
		for(register int i = 1;i <= n;++i)
		{
			scanf(" %c",&ch);
			sum += cnt[ch - '0'];  //先全部加起来
		}
		for(register int i = n;i >= 1;--i)
		{
			cur = 9;
			if(i == 1)  //特判
			{
				while(sum != cnt[cur])
					--cur;
				putchar(cur + '0');
				break;
			}
			while(!judge(i - 1,sum - cnt[cur]))
				--cur;
			sum -= cnt[cur];  //排除不能的
			putchar(cur + '0');
		}
		puts("");
	}
	return 0;
}

T3：游戏

题目描述

Guyu Guo和Tube Lu正在玩一个游戏：Lu默想一个1和n 之间的数x，然后Guo尝试猜出这个数。
Guo能提出m个这样的问题： “未知数是否能被yi整除？”
游戏按照如下流程进行：Guo先给出他想问的全部m个问题，然后Lu对所有问题依次以“是”或“否”作答。得到m个问题的答案之后，Guo就要给出他的猜测。
Guo写了一个程序帮他以最优的方式提出这m个问题，现在他想知道在保证得到一个确定的答案下，最少可以问多少个问题，即m的最小值。但是Guo正忙于吃漂亮学姐送他的糖果而无暇改代码（送糖果的学姐十分多，以至于有许多糖果快要过期了），所以他找到了你，希望你来帮他解决这个问题。

输入

一行，一个整数n

输出

一行，一个整数m

样例输入

【样例输入1】

4

【样例输入2】

8

样例输出

【样例输出1】

3

【样例输出2】

6

分析：枚举及数学

由于一次性提出m个问题，然后得到回答，所以只能通过问题来确定最终可能的所有情况。
将n以内所有的质数求出来，用布尔类型存放
其实，推一推后，答案就是所有质数可能出现的次数，所以答案为所有质数的幂次<=n的个数
——————————————————————————————

CODE：

#include
#include
#include
#include
#include
using namespace std;
bool f[100010];
long long w;
int n,ans;
int main()
{
	freopen("game.in","r",stdin);
	freopen("game.out","w",stdout);
	cin>>n;
	memset(f,false,sizeof f);
	f[1] = true;
	ans = 0;
	for(int i = 2;i <= n;i++)  //找质数
		if(f[i] == false)
			for(int j = 2;j <= n / i;j++)
				f[i * j] = true;  //布尔存放
	for(int i = 2;i <= n;i++)
		if(f[i] == false)
		{
			w = i;
			while(w <= n)
			{
				ans++;  //出现次数
				w *= i;  //幂次
			}
		}
	cout<<ans;
}

T4：hack的游戏

题目描述

Codefires round马上就要结束了！ZCC已经通过做题得到了C分。但他惊讶地发现，房间里的其他选手也都解决了最难的题。ZCC根据经验断定大多数的选手都会FST的！当然，除去rating最高的选手Memset137。在此之前，ZCC想要hack他们来使他的得分更高。除了ZCC，房间里有N个选手，他们已经被按照rating从小到大排序了(所以Memset137是排在第N个的选手)。当ZCC成功hack了第i个选手时，他会获得i分的收入。你可以假设ZCC hack技术高超，百发百中，可以hack除了Memset137和自己以外的所有选手，而且在此期间没有其他选手干扰。
由于ZCC有着谦虚的美德，他不想让自己的得分太高。ZCC想要知道，存在着多少种不同的选择一些人hack的方案，使得他的得分在L和R(C≤L≤R 显然答案会很大，请输出答案对998244353取模后的结果。

输入

一行，四个整数n,c,l,r分别表示n个选手，当前分数为c，希望得分在l到r之间

输出

输出一行，方案数

样例输入

Sample Input1:

3 0 1 2

Sample Input2:

5 13 14 17

Sample Input3:

100 0 23 59

样例输出

Sample Output1:

2

Sample Output2:

6

Sample Output3:

90567

分析：DP

首先，设f[i][j]为前i个数选了若干个的和为j的方案数，
那么容易推出f[i][j]=f[i-1][j]+f[i-1][j-i]
但是，这样做空间复杂度为O(NC),绝对会炸
所以，发现前m个数的和为m（m-1）/2
令m（m-1）/2=n，则m只有根号n级别，那么说明最多选根号n个数
故可以转成f[i][j]=f[i-1,j-i]+f[i,j-i] (为选了i个数和为j的方案数)
——————————————————————————————

CODE：

#include
#include
#include
#include
using namespace std;
int n,c,l,r,dp[2][10000];
int main()
{
	freopen("hack.in","r",stdin);
    freopen("hack.out","w",stdout);
        scanf("%d%d%d%d",&n,&c,&l,&r);
        l -= c,r = min(r - c,n - 1);
        memset(dp,0,sizeof(dp));
        dp[0][0] = 1;
        int ans = l <= 0 ? 1 : 0;
        for(int i = 1;(i + 1) * i / 2 <= r;i++)
        {  //dp过程
            for(int j = (1 + i) * i / 2;j <= r;j++)
            {
                dp[i & 1][j] = (dp[i & 1][j - i] + dp[(i - 1) & 1][j - i]) % 998244353;
                if(l <= j && j <= r)
                    ans = (ans + dp[i & 1][j]) % 998244353; //取%
            }
            memset(dp[(i - 1) & 1],0,sizeof(dp[(i - 1) & 1]));  //重新初始化
        }
        printf("%d\n",ans);
}

无了……