12.【基础】手写体数字图像聚类--KMeans

本文所有实现代码均来自《Python机器学习及实战》

#-*- coding:utf-8 -*-

#分别导入numpy、matplotlib、pandas，用于数学运算、作图以及数据分析
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd 

#第一步：使用pandas读取训练数据和测试数据
digits_train = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra',header=None)
digits_test = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes',header=None)

#第二步：已知原始数据有65个特征值，前64个是像素特征，最后一个是每个图像样本的数字类别
#从训练集和测试集上都分离出64维度的像素特征和1维度的数字目标
X_train = digits_train[np.arange(64)]
y_train = digits_train[64]
X_test = digits_test[np.arange(64)]
y_test = digits_test[64]

#第三步：使用KMeans模型进行训练并预测
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=10)
kmeans.fit(X_train)
kmeans_y_predict = kmeans.predict(X_test)

#第四步：评估KMeans模型的性能
#如何评估聚类算法的性能？
#1.Adjusted Rand Index(ARI) 适用于被用来评估的数据本身带有正确类别的信息，ARI指标和计算Accuracy的方法类似
#2.Silhouette Coefficient(轮廓系数) 适用于被用来评估的数据没有所属类别 同时兼顾了凝聚度和分散度，取值范围[-1,1],值越大，聚类效果越好
from sklearn.metrics import adjusted_rand_score
print 'The ARI value of KMeans is',adjusted_rand_score(y_test,kmeans_y_predict)
#到此为止，手写体数字图像聚类--kmeans学习结束，下面单独讨论轮廓系数评价kmeans的性能

#****************************************************************************************************
#拓展学习：利用轮廓系数评价不同累簇数量(k值)的K-means聚类实例
from sklearn.metrics import silhouette_score
#分割出3*2=6个子图，并且在1号子图作图 subplot(nrows, ncols, plot_number)
plt.subplot(3,2,1)
#初始化原始数据点
x1 = np.array([1,2,3,1,5,6,5,5,6,7,8,9,7,9])
x2 = np.array([1,3,2,2,8,6,7,6,7,1,2,1,1,3])
# a = [1,2,3] b = [4,5,6] zipped = zip(a,b) 输出为元组的列表[(1, 4), (2, 5), (3, 6)]
X = np.array(zip(x1,x2)).reshape(len(x1),2)
#X输出为：array([[1, 1],[2, 3],[3, 2],[1, 2],...,[9, 3]])
#在1号子图作出原始数据点阵的分布
plt.xlim([0,10])
plt.ylim([0,10])
plt.title('Instances')
plt.scatter(x1,x2)
colors = ['b','g','r','c','m','y','k','b']
markers = ['o','s','D','v','^','p','*','+']
clusters = [2,3,4,5,8]
subplot_counter = 1
sc_scores = []

for t in clusters:
    subplot_counter += 1
    plt.subplot(3,2,subplot_counter)
    kmeans_model = KMeans(n_clusters=t).fit(X)
    for i,l in enumerate(kmeans_model.labels_):
        plt.plot(x1[i],x2[i],color=colors[l],marker=markers[l],ls='None')
        plt.xlim([0,10])
        plt.ylim([0,10])   
    sc_score = silhouette_score(X,kmeans_model.labels_,metric='euclidean')
    sc_scores.append(sc_score)
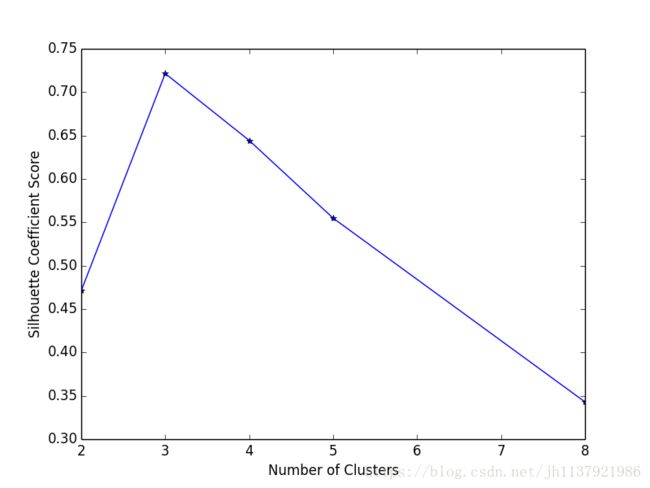
    #绘制轮廓系数与不同类簇数量的直观显示图
    plt.title('K=%s,silhouette coefficient = %0.03f'%(t,sc_score))
#绘制轮廓系数与不同类簇数量的关系曲线

plt.figure() #此处必须空一行，表示在for循环结束之后执行！！！
plt.plot(clusters,sc_scores,'*-') #绘制折线图时的样子
plt.xlabel('Number of Clusters')
plt.ylabel('Silhouette Coefficient Score')
plt.show()
#****************************************************************************************************

#总结：
#k-means聚类模型所采用的迭代式算法，直观易懂并且非常实用，但是有两大缺陷
#1.容易收敛到局部最优解，受随机初始聚类中心影响，可多执行几次k-means来挑选性能最佳的结果
#2.需要预先设定簇的数量，通过“肘部观察法”，选择拐点对应的k值

补充：

• 由折线图可知，在k=3时 ，对应的轮廓系数值是最大的，那么我们将采用k=3时的训练模型，为此例中最佳的模型；
• 值得一提的是，这里的折线图纵轴是轮廓系数，而不是“肘部”观察法采用的距离平方和的均值，二者不要混淆，下一讲中会详细讲解如何使用“肘部”观察法。