特征选择之基于相关性的特征选择（CFS）

此为本人学习笔记，转载请劳烦告知！

特征选择

特征抽取整合原始特征，这样可能产生一些新的特征，而特征选择是去除无关紧要或庸余的特征，仍然还保留其他原始特征。特征提取主要用于图像分析，信号处理和信息检索领域，在这些领域，模型精确度比模型可解释性要重要；特征选择主要用于数据挖掘，像文本挖掘，基因分析和传感器数据处理。今天主要做的是特征选择。

特征选择定义：检测相关特征，摒弃冗余特征，以获得特征子集，从而以最小的性能损失更好地描述给出的问题。

特征选择方法

滤波器（filter）

单变量滤波
优点：计算简单快速，能处理极大量的数据集，与分类器独立
缺点：不与分类器交互，忽略特征相关性
方法：卡方，欧氏距离，t检验，信息增益或增益比率
多变量滤波
优点：能捕捉模型特征相关性，分类器独立，比封装方法计算复杂度小
缺点：比单变量滤波慢，和单变量滤波相比不能处理大量数据，忽略与分类器的交互
方法：基于相关性的特征选择（correlation-based feature selection,CFS,Hall,1999），最小冗余最大相关性（MRMR，Ding and Peng,2003），马尔科夫覆盖过滤器（Markov blanket filter,MBF, Koller and Sahami, 1996）,快速基于相关性的特征选择（Fast correlation-based feature selection,FCBF, Yu and Liu, 2004），relief-F算法

封装（wrapper）

确定性算法
优点：简单，与分类器交互，能捕捉特征相关性，和随机算法相比计算开销小
缺点：相比随机算法，更倾向于稳定在局部最优（贪心搜索），有过度拟合风险，依赖分类器选择特征
方法：序列化前向选择（Sequential forward selection,SFS），序列化后向消除（Sequential backward elimination,SBE,Kittler,1978）,束搜索（beam search, Siedelecky and Sklansky, 1988）
随机性算法
优点：更少趋向于稳定在局部最优，和分类器交互，能捕捉特征相关性
缺点：计算开销大，依赖于分类器选择，与确定性算法相比有高度过拟合风险
方法：模拟退火（simulated annealing），随机爬坡法（randomized hill climbing,Skalak,1994），遗传算法（GA，Holland,1975），分布式估计算法（estimation of distribution algrithms,Inza et al.,2000）

###集成方法（Embedded）

优点：与分类器交互，比wrapper方法计算开销小，能捕捉特征相关性
缺点：依赖分类器选择特征
方法：决策树，随机森林，加权贝叶斯（Duda et al.,2001），利用SVM加权向量的特征选择（feature selection using the weight vector of SVM, Guyon et al., 2002; Weston et al., 2003）（？递归特征消除）

一般选择变量个数：

• N < 10，选择75%的特征；
• 10 < N < 75，选择40%的特征；
• 75 < N < 100，选择10%的特征
• N > 100，选择3%的特征

N为特征变量个数。

CFS(correlation-based feature selection)

特征估计

CFS估计特征子集并对特征子集而不是单个特征进行排秩。
CFS的核心是采用启发的方式评估特征子集的价值。
启发方式基于的假设：
好的特征子集包含与类高度相关的特征，但特征之间彼此不相关。
启发式方程：
$$Meri{t}_s=\frac{k\overline{r_{cf}}}{\sqrt{k+k(k-1)\overline{r_{ff}}}}$$
$Meri{t}_s$为包含k个特征的特征子集S的启发式’merit’，$\overline{r_{cf}}$为特征-类平均相关性，$\overline{r_{ff}}$为特征-特征平均相关性。r为Pearson相关系数，所有的变量需要标准化。
启发式方法去除对类预测不起作用的特征变量，并识别与其他特征高度相关的特征。

搜索特征子集空间

CFS首先从训练集中计算特征-类和特征-特征相关矩阵，然后用最佳优先搜索（best first search）搜索特征子集空间。也可使用其他的搜索方法，包括前向选择(forward selection)，后向消除(backward elimination)。前向选择刚开始没有特征，然后贪心地增加一个特征直到没有合适的特征加入。后向消除开始有全部特征，然后每一次贪心地去除一个特征直到估计值不再降低。最佳优先搜索和前两种搜索方法差不多。可以开始于空集或全集，以空集M为例，开始时没有特征选择，并产生了所有可能的单个特征；计算特征的估计值（由merit值表示），并选择merit值最大的一个特征进入M，然后选择第二个拥有最大的merit值的特征进入M，如果这两个特征的merit值小于原来的merit值，则去除这个第二个最大的merit值的特征，然后在进行下一个，这样依次递进，找出使merit最大的特征组合。
它的时间复杂度为$m\times \frac{n^2-n}{2}$.

流程图

案例分析

假设一个数据集拥有4个特征变量，它的相关矩阵如下图：

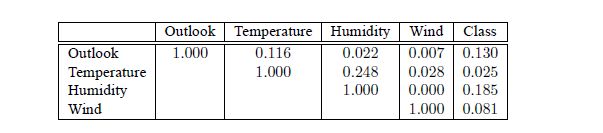
用相关性函数的前向选择搜索计算如下：

最终得到的结果为[Outlook,Humidity,Wind]。

代码实现：FeatureSelectionsAndExtractions

参考文献
【Yvan Saeys, Inaki Inza and Pedro Larranaga】A review of feature selection techniques in bioinformatics
【Mark A. Hall】Correlation-based Feature Selection for Discrete and Numeric Class Machine Learning
【Mark A. Hall】correlation-based feature selection for machine learning
【Barry O’Sullivan, Cork, Ireland】Feature Selection for High-Dimensional Data