DeepLearing学习笔记-改善深层神经网络(第二周作业-优化方法)
0- 背景:
本文将介绍几种常用的优化方法,用以加快神经网络的学习速度
本文需要用到的库如下:
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
from opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'1- 梯度下降法
梯度下降是每次处理完 m 个样本后对参数进行一次更新操作,也叫做Batch Gradient Descent。
对于L层模型,梯度下降法对于各层参数的更新: l=1,...,L :
L表示层数, α 是学习率。所有的这些参数都存在 parameters 字典中。注意,循环是从L1开始。
# GRADED FUNCTION: update_parameters_with_gd
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
Update parameters using one step of gradient descent
Arguments:
parameters -- python dictionary containing your parameters to be updated:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients to update each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
learning_rate -- the learning rate, scalar.
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Update rule for each parameter
for l in range(L):
### START CODE HERE ### (approx. 2 lines)
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads['dW' + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads['db' + str(l+1)]
### END CODE HERE ###
return parameters测试代码:
parameters, grads, learning_rate = update_parameters_with_gd_test_case()
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))测试代码运行如下:
W1 = [[ 1.63535156 -0.62320365 -0.53718766]
[-1.07799357 0.85639907 -2.29470142]]
b1 = [[ 1.74604067]
[-0.75184921]]
W2 = [[ 0.32171798 -0.25467393 1.46902454]
[-2.05617317 -0.31554548 -0.3756023 ]
[ 1.1404819 -1.09976462 -0.1612551 ]]
b2 = [[-0.88020257]
[ 0.02561572]
[ 0.57539477]]梯度下降的一种变体是随机梯度下降法Stochastic Gradient Descent (SGD)。这等同于mini-batch中每个mini-batch只有一个样本的梯度下降法。此时,梯度下降的更新法则就变成,每个样本都要计算一次,而不是此前的对整个样本集计算一次。
两者代码如下:
- (Batch) Gradient Descent:
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
# Forward propagation
a, caches = forward_propagation(X, parameters)
# Compute cost.
cost = compute_cost(a, Y)
# Backward propagation.
grads = backward_propagation(a, caches, parameters)
# Update parameters.
parameters = update_parameters(parameters, grads)
- Stochastic Gradient Descent:
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
for j in range(0, m):
# Forward propagation
a, caches = forward_propagation(X[:,j], parameters)
# Compute cost
cost = compute_cost(a, Y[:,j])
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters.
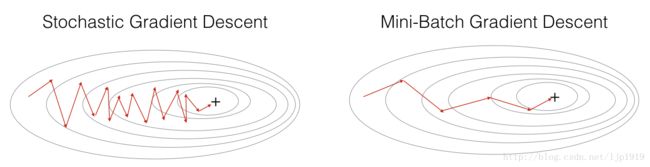
parameters = update_parameters(parameters, grads)在随机梯度下降中, 我们对于每个样本都更新梯度。当训练集很大时,这种方法可以明显提高运行速度,但是参数会沿着最小方向震荡,而不是平滑地收敛。
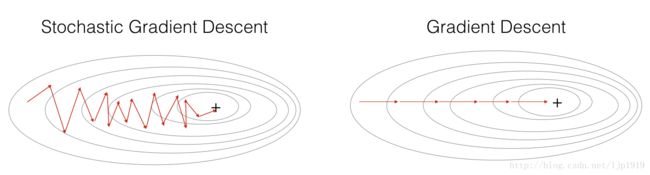
“+” 表示代价最小值。SGD在收敛前出现很多震荡,但是由于每步都只有一个样本,所以每步都比梯度下降GD要来得快。 (vs. the whole batch for GD).
注意 SGD 共需要三个循环:
1. 最外层的迭代次数
2. m 个训练样本
3. 每层参数的更新 ( (W[1],b[1]) to (W[L],b[L]) )
在实际情况中,我们一般是折中,即所谓的 Mini-batch gradient descent。将整体的训练集分成子数据集,然后每个子训练集计算一次梯度下降。
“+” 表示最小代价值。
谨记:
- gradient descent, mini-batch gradient descent 和 stochastic gradient descent之间的区别在于梯度更新所用到的样本数据量。
- 超参数学习率 α 是需要调整获取到
- mini-batch的尺寸也是调整获取到的,所以也是一个超参数。一般情况下这种方式比另外两者更好,特别是当训练集特别大的时候。
2 - Mini-Batch梯度下降
mini-batches用于训练集 (X, Y),一般有以下两个步骤:
Shuffle(洗牌): 随机洗牌的方式将训练样本的数据顺序随机打散,注意:X和Y的随机要一致,否则Y值不能与X匹配,出现张冠李戴。随机化的洗牌操作能够将样本切分成不同的mini-batches。洗牌方式如下图所示:
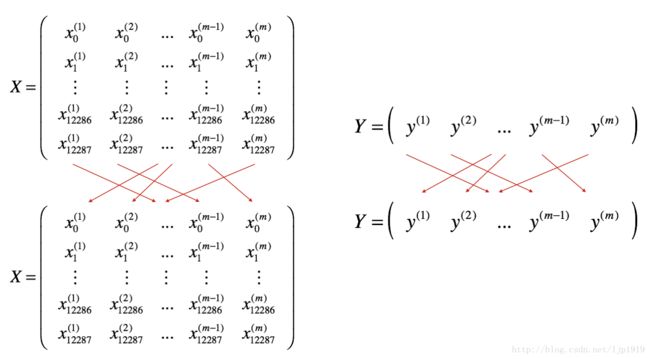
Partition(分割): 将已经随机化的数据集(X, Y)分割成
mini_batch_size(本文= 64)大小的子数据集。尾部的数据可能小于一个mini_batch_size,所以对于最后一个mini-batch要注意处理。
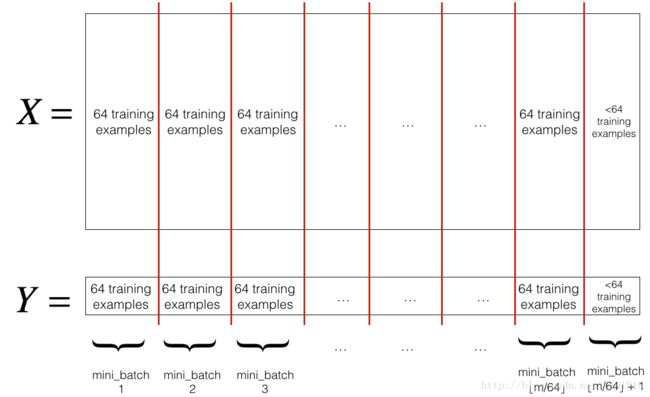
我们定义 random_mini_batches函数来实现上述功能。在采用索引切片的时候,操作 1st and 2nd mini-batches如下,其他依次。
first_mini_batch_X = shuffled_X[:, 0 : mini_batch_size]
second_mini_batch_X = shuffled_X[:, mini_batch_size : 2 * mini_batch_size]
...当样本数无法被mini_batch_size整除的时候,最后一个mini-batch< mini_batch_size=64。 ⌊s⌋ 表示 s 向下取整 (Python中实现:math.floor(s))。所以 ⌊mmini_batch_size⌋ 个mini-batches中的样本数量是= 64,最后一个min-batch中样本数量= ( m−mini_batch_size×⌊mmini_batch_size⌋ )。
代码实现如下:
# GRADED FUNCTION: random_mini_batches
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
mini_batch_size -- size of the mini-batches, integer
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
np.random.seed(seed) # To make your "random" minibatches the same as ours
m = X.shape[1] # number of training examples
#print("m=",m)
mini_batches = []
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
#print("num_complete_minibatches=",num_complete_minibatches)
for k in range(0, num_complete_minibatches):
### START CODE HERE ### (approx. 2 lines)
mini_batch_X = shuffled_X[:, k * mini_batch_size : (k+1) * mini_batch_size]
mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k+1) * mini_batch_size]
### END CODE HERE ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
#print(k)
# Handling the end case (last mini-batch < mini_batch_size)
# 尾数处理
#print(num_complete_minibatches * mini_batch_size)
if m % mini_batch_size != 0:
### START CODE HERE ### (approx. 2 lines)
mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : ]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : ]
### END CODE HERE ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches代码测试如下:
X_assess, Y_assess, mini_batch_size = random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess, Y_assess, mini_batch_size)
print ("shape of the 1st mini_batch_X: " + str(mini_batches[0][0].shape))
print ("shape of the 2nd mini_batch_X: " + str(mini_batches[1][0].shape))
print ("shape of the 3rd mini_batch_X: " + str(mini_batches[2][0].shape))
print ("shape of the 1st mini_batch_Y: " + str(mini_batches[0][1].shape))
print ("shape of the 2nd mini_batch_Y: " + str(mini_batches[1][1].shape))
print ("shape of the 3rd mini_batch_Y: " + str(mini_batches[2][1].shape))
print ("mini batch sanity check: " + str(mini_batches[0][0][0][0:3]))测试代码运行输出结果如下:
shape of the 1st mini_batch_X: (12288, 64)
shape of the 2nd mini_batch_X: (12288, 64)
shape of the 3rd mini_batch_X: (12288, 20)
shape of the 1st mini_batch_Y: (1, 64)
shape of the 2nd mini_batch_Y: (1, 64)
shape of the 3rd mini_batch_Y: (1, 20)
mini batch sanity check: [ 0.90085595 -0.7612069 0.2344157 ]PS:一般mini-batch size的取值是 2n ,如 16, 32, 64, 128等
Momentum(动量梯度下降法)
由于min-batch梯度下降法是在看过训练集的一部分子数据集之后,就开始了参数的更新,那么就会在参数更新过程中出现偏差震荡。采用动量梯度下降法可以减缓震荡的出现。
momentum方式是在参数更新时候,参考历史的参数值,以平滑参数的更新。我们以变量 v 存储梯度变化的历史方向。一般情况下,这个 v 值是历史梯度值的指数加权平均结果。我们可以将 v 视为球下坡滚动的”velocity”。
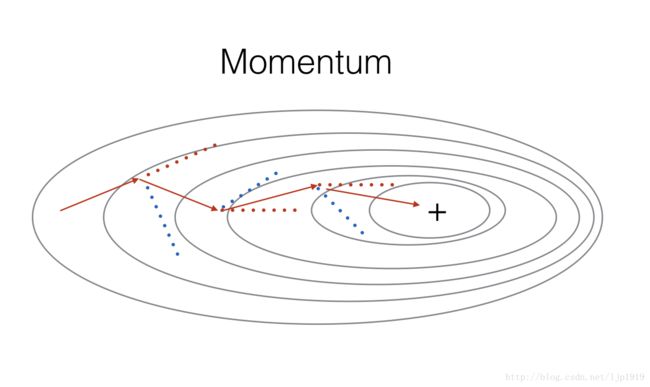
红色箭头表示在momentum作用下每个mini-batch梯度下降的方向,而蓝色则是没有momentum作用的mini-batch梯度下降方向。
velocity值初始化:
velocity, v ,在Python中是一个字典,初始为0矩阵,其尺寸与 grads 一致:
for l=1,...,L :
v["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
v["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])initialize_velocity代码实现如下:
# GRADED FUNCTION: initialize_velocity
def initialize_velocity(parameters):
"""
Initializes the velocity as a python dictionary with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
Returns:
v -- python dictionary containing the current velocity.
v['dW' + str(l)] = velocity of dWl
v['db' + str(l)] = velocity of dbl
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
#print(parameters['W1'].shape)
# Initialize velocity
for l in range(L):
### START CODE HERE ### (approx. 2 lines)
v["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0], parameters['W' + str(l+1)].shape[1]))
v["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0], parameters['b' + str(l+1)].shape[1]))
### END CODE HERE ###
return v初始化函数测试:
parameters = initialize_velocity_test_case()
v = initialize_velocity(parameters)
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))测试结果如下:
v["dW1"] = [[ 0. 0. 0.]
[ 0. 0. 0.]]
v["db1"] = [[ 0.]
[ 0.]]
v["dW2"] = [[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
v["db2"] = [[ 0.]
[ 0.]
[ 0.]]带momentum的参数更新:
更新规则如下:
for l=1,...,L :
其中 L 表示层数, β 是momentum值, α 是学习率。 这些参数都存于 parameters 字典中。注意 W[1] and b[1] 是从第1层开始的。
update_parameters_with_momentum函数代码实现如下:
# GRADED FUNCTION: update_parameters_with_momentum
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
v['dW' + str(l)] = ...
v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar
Returns:
parameters -- python dictionary containing your updated parameters
v -- python dictionary containing your updated velocities
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Momentum update for each parameter
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
# compute velocities
v["dW" + str(l+1)] = beta * v["dW" + str(l+1)] + (1-beta) * grads['dW' + str(l+1)]
v["db" + str(l+1)] = beta * v["db" + str(l+1)] + (1-beta) * grads['db' + str(l+1)]
# update parameters
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v["db" + str(l+1)]
### END CODE HERE ###
return parameters, v函数测试代码:
parameters, grads, v = update_parameters_with_momentum_test_case()
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta = 0.9, learning_rate = 0.01)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))测试结果如下:
W1 = [[ 1.62544598 -0.61290114 -0.52907334]
[-1.07347112 0.86450677 -2.30085497]]
b1 = [[ 1.74493465]
[-0.76027113]]
W2 = [[ 0.31930698 -0.24990073 1.4627996 ]
[-2.05974396 -0.32173003 -0.38320915]
[ 1.13444069 -1.0998786 -0.1713109 ]]
b2 = [[-0.87809283]
[ 0.04055394]
[ 0.58207317]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907]
[ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902]
[-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608]
[-0.03967535 -0.06871727 -0.08452056]
[-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[ 0.02344157]
[ 0.16598022]
[ 0.07420442]]注意 :
- velocity初始化为zeros,所以算法需要迭代一定次数以建立起速度,实现每次迭代的bigger steps。
- 当 β=0 ,则退化成标准的梯度下降法。
β 值得选取:
- β 越大,历史梯度值引入到当前值的权重越大,更新就会越平滑。但是如果 β 太大,则会导致更新平滑过度。
- β 一般取值在0.8 到 0.999之间,常取 β=0.9 。
- 可以通过尝试几个 β 值,然后看哪个值在降低cost function J 效果最好,来获取最优值。
4 - Adam算法
Adam算法应该是目前在神经网络领域最有效的优化算法了,该算法联合了RMSProp算法和Momentum算法。
Adam算法流程:
1.先计算历史梯度的指数加权平均值,存于变量 v , vcorrected 表示校正后的值。
2. 计算历史梯度平方值的指数加权平均值,存于变量 s , scorrected 表示校正后的值。
3. 联合”1” and “2”更新参数
更新规则如下, for l=1,...,L :
其中:
- t 表示迭代的次数
- L 表示层数
- β1 and β2 都是超参数,控制指数加权的权重
- α 是学习率
- ε 是一个很小的值,为了避免除0操作
变量 v,s 的初始化如下:
for l=1,...,L :
v["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
v["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])
s["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
s["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])
Adam的初始化代码:
# GRADED FUNCTION: initialize_adam
def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
Returns:
v -- python dictionary that will contain the exponentially weighted average of the gradient.
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
s = {}
# Initialize v, s. Input: "parameters". Outputs: "v, s".
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
v["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0], parameters['W' + str(l+1)].shape[1]))
v["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0], parameters['b' + str(l+1)].shape[1]))
s["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0], parameters['W' + str(l+1)].shape[1]))
s["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0], parameters['b' + str(l+1)].shape[1]))
### END CODE HERE ###
return v, s代码测试:
parameters = initialize_adam_test_case()
v, s = initialize_adam(parameters)
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))
print("s[\"dW1\"] = " + str(s["dW1"]))
print("s[\"db1\"] = " + str(s["db1"]))
print("s[\"dW2\"] = " + str(s["dW2"]))
print("s[\"db2\"] = " + str(s["db2"]))
测试代码输出:
v["dW1"] = [[ 0. 0. 0.]
[ 0. 0. 0.]]
v["db1"] = [[ 0.]
[ 0.]]
v["dW2"] = [[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
v["db2"] = [[ 0.]
[ 0.]
[ 0.]]
s["dW1"] = [[ 0. 0. 0.]
[ 0. 0. 0.]]
s["db1"] = [[ 0.]
[ 0.]]
s["dW2"] = [[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
s["db2"] = [[ 0.]
[ 0.]
[ 0.]]Adam算法实现:
# GRADED FUNCTION: update_parameters_with_adam
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
"""
Update parameters using Adam
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates
beta2 -- Exponential decay hyperparameter for the second moment estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters) // 2 # number of layers in the neural networks
v_corrected = {} # Initializing first moment estimate, python dictionary
s_corrected = {} # Initializing second moment estimate, python dictionary
# Perform Adam update on all parameters
for l in range(L):
# Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
### START CODE HERE ### (approx. 2 lines)
v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1-beta1) * grads['dW' + str(l+1)]
v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1-beta1) * grads['db' + str(l+1)]
### END CODE HERE ###
# Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
### START CODE HERE ### (approx. 2 lines)
v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)]/(1-np.power(beta1,t))
v_corrected["db" + str(l+1)] = v["db" + str(l+1)]/(1-np.power(beta1,t))
### END CODE HERE ###
# Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
### START CODE HERE ### (approx. 2 lines)
s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1-beta2) * np.power(grads['dW' + str(l+1)],2)
s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1-beta2) * np.power(grads['db' + str(l+1)],2)
### END CODE HERE ###
# Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
### START CODE HERE ### (approx. 2 lines)
s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)]/(1-np.power(beta2,t))
s_corrected["db" + str(l+1)] = s["db" + str(l+1)]/(1-np.power(beta2,t))
### END CODE HERE ###
# Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
### START CODE HERE ### (approx. 2 lines)
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v_corrected["dW" + str(l+1)]/(np.sqrt(s_corrected["dW" + str(l+1)])+epsilon)
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v_corrected["db" + str(l+1)]/(np.sqrt(s_corrected["db" + str(l+1)])+epsilon)
### END CODE HERE ###
return parameters, v, sAdam算法测试:
parameters, grads, v, s = update_parameters_with_adam_test_case()
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s, t = 2)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))
print("s[\"dW1\"] = " + str(s["dW1"]))
print("s[\"db1\"] = " + str(s["db1"]))
print("s[\"dW2\"] = " + str(s["dW2"]))
print("s[\"db2\"] = " + str(s["db2"]))测试代码运行如下:
W1 = [[ 1.63178673 -0.61919778 -0.53561312]
[-1.08040999 0.85796626 -2.29409733]]
b1 = [[ 1.75225313]
[-0.75376553]]
W2 = [[ 0.32648046 -0.25681174 1.46954931]
[-2.05269934 -0.31497584 -0.37661299]
[ 1.14121081 -1.09244991 -0.16498684]]
b2 = [[-0.88529979]
[ 0.03477238]
[ 0.57537385]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907]
[ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902]
[-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608]
[-0.03967535 -0.06871727 -0.08452056]
[-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[ 0.02344157]
[ 0.16598022]
[ 0.07420442]]
s["dW1"] = [[ 0.00121136 0.00131039 0.00081287]
[ 0.0002525 0.00081154 0.00046748]]
s["db1"] = [[ 1.51020075e-05]
[ 8.75664434e-04]]
s["dW2"] = [[ 7.17640232e-05 2.81276921e-04 4.78394595e-04]
[ 1.57413361e-04 4.72206320e-04 7.14372576e-04]
[ 4.50571368e-04 1.60392066e-07 1.24838242e-03]]
s["db2"] = [[ 5.49507194e-05]
[ 2.75494327e-03]
[ 5.50629536e-04]]5 - Model with different optimization algorithms
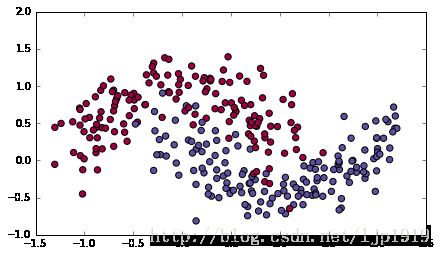
对于上述几种优化算法的测试,在这里我们采用 “moons” 数据集。
数据加载:
train_X, train_Y = load_dataset()对于一个3层的神经网络,我们将采用下述三种优化算法来训练:
- Mini-batch Gradient Descent: 通过调用:
update_parameters_with_gd()来实现
- Mini-batch Momentum: 通过调用:
initialize_velocity()和update_parameters_with_momentum()来实现。
- Mini-batch Adam: 通过调用:
initialize_adam()和update_parameters_with_adam()来实现
模型代码:
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 10000, print_cost = True):
"""
3-layer neural network model which can be run in different optimizer modes.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
layers_dims -- python list, containing the size of each layer
learning_rate -- the learning rate, scalar.
mini_batch_size -- the size of a mini batch
beta -- Momentum hyperparameter
beta1 -- Exponential decay hyperparameter for the past gradients estimates
beta2 -- Exponential decay hyperparameter for the past squared gradients estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
num_epochs -- number of epochs
print_cost -- True to print the cost every 1000 epochs
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(layers_dims) # number of layers in the neural networks
costs = [] # to keep track of the cost
t = 0 # initializing the counter required for Adam update
seed = 10 # For grading purposes, so that your "random" minibatches are the same as ours
# Initialize parameters
parameters = initialize_parameters(layers_dims)
# Initialize the optimizer
if optimizer == "gd":
pass # no initialization required for gradient descent
elif optimizer == "momentum":
v = initialize_velocity(parameters)
elif optimizer == "adam":
v, s = initialize_adam(parameters)
# Optimization loop
for i in range(num_epochs):
# Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epoch
seed = seed + 1
minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# Forward propagation
a3, caches = forward_propagation(minibatch_X, parameters)
# Compute cost
cost = compute_cost(a3, minibatch_Y)
# Backward propagation
grads = backward_propagation(minibatch_X, minibatch_Y, caches)
# Update parameters
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
elif optimizer == "adam":
t = t + 1 # Adam counter
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
t, learning_rate, beta1, beta2, epsilon)
# Print the cost every 1000 epoch
if print_cost and i % 1000 == 0:
print ("Cost after epoch %i: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
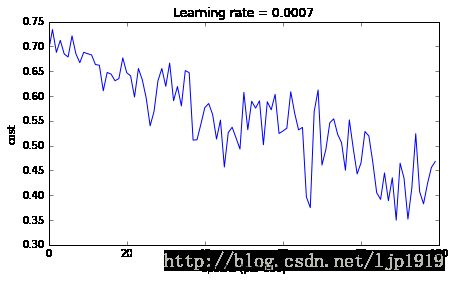
plt.title("Learning rate = " + str(learning_rate))
plt.show()
return parameters5-1 Mini-batch Gradient descent
代码如下:
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")
# Predict
predictions = predict(train_X, train_Y, parameters)
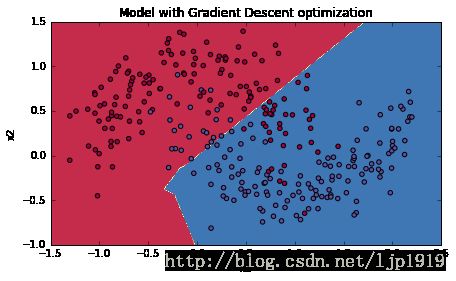
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)运行结果如下:
Cost after epoch 0: 0.690736
Cost after epoch 1000: 0.685273
Cost after epoch 2000: 0.647072
Cost after epoch 3000: 0.619525
Cost after epoch 4000: 0.576584
Cost after epoch 5000: 0.607243
Cost after epoch 6000: 0.529403
Cost after epoch 7000: 0.460768
Cost after epoch 8000: 0.465586
Cost after epoch 9000: 0.464518Accuracy: 0.796666666667
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.maximum.reduce will be axis=0, not the current None, to match np.maximum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.minimum.reduce will be axis=0, not the current None, to match np.minimum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
5-2 Mini-batch gradient descent with momentum
代码如下:
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
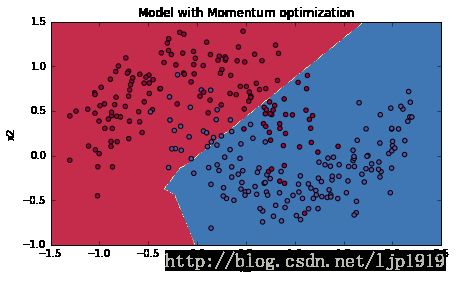
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)运行结果如下:
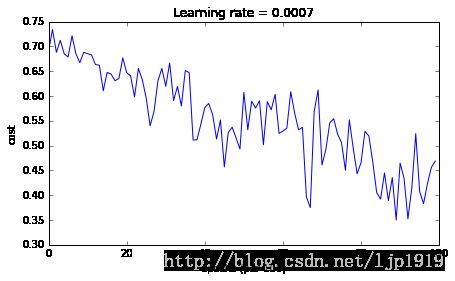
Cost after epoch 0: 0.690741
Cost after epoch 1000: 0.685341
Cost after epoch 2000: 0.647145
Cost after epoch 3000: 0.619594
Cost after epoch 4000: 0.576665
Cost after epoch 5000: 0.607324
Cost after epoch 6000: 0.529476
Cost after epoch 7000: 0.460936
Cost after epoch 8000: 0.465780
Cost after epoch 9000: 0.464740Accuracy: 0.796666666667
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.maximum.reduce will be axis=0, not the current None, to match np.maximum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.minimum.reduce will be axis=0, not the current None, to match np.minimum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
5-3 Mini-batch with Adam mode
代码如下:
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
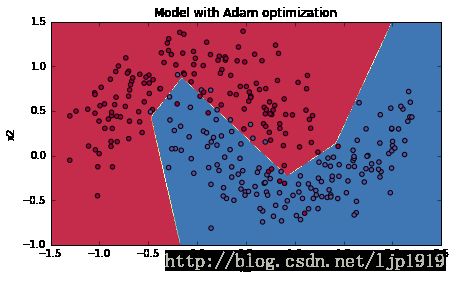
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)运行结果如下:
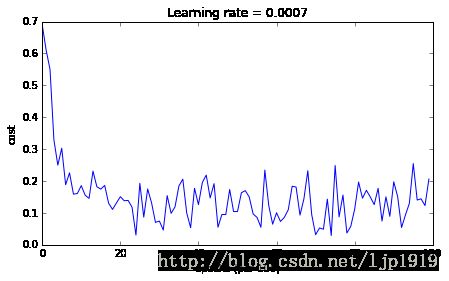
Cost after epoch 0: 0.690552
Cost after epoch 1000: 0.185567
Cost after epoch 2000: 0.150852
Cost after epoch 3000: 0.074454
Cost after epoch 4000: 0.125936
Cost after epoch 5000: 0.104235
Cost after epoch 6000: 0.100552
Cost after epoch 7000: 0.031601
Cost after epoch 8000: 0.111709
Cost after epoch 9000: 0.197648Accuracy: 0.94
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.maximum.reduce will be axis=0, not the current None, to match np.maximum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
c:\users\jason\appdata\local\programs\python\python35\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.minimum.reduce will be axis=0, not the current None, to match np.minimum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
5-4 总结:
| optimization method | accuracy | cost shape |
| Gradient descent | 79.7% | oscillations |
| Momentum | 79.7% | oscillations |
| Adam | 94% | smoother |
Momentum一般都是有助于提升速度,但是当学习率较小,数据集相对简单的时候,其性能的优越性没有太明显。我们在优化算法中看到的那些较大的震荡是由于一些minibatches 相对更加复杂所造成的。
从运行结果可以看出,Adam算法比mini-batch gradient descent 和 Momentum都要显得优越。对于model如果在简单数据集上,迭代次数更多的话,这三种优化算法都会产生较好的结果,但是我们也可以看出,Adam算法收敛得更快些。
Adam算法的优点:
- 内存要求低 (尽管比gradient descent 和 gradient descent with momentum要高些)
- 一般微调超参数就可以获得较好的结果(除了 α )