PCA

PCA 数据降维

一、主成分的计算步骤

1- 对原始数据进行标准化处理，消除量纲

2- 计算标准化数据的相关系数矩阵

3- 计算标准化数据的相关系数矩阵的特征根及对应的特征向量

4- 选出最大的特征根，对应的特征向量等于第一主成分的系数；选出第二大的特征根，对应的特征向量等于 第二主成分的系数；以此类推

5- 计算累积贡献率，选择恰当的主成分个数

6- 解释主成分：写出前k个主成分的表达式

7- 确定各样本的主成分得分

8- 根据主成分得分的数据，做进一步的统计分析

二、R语言实现

• 载入需要的数据包 psych

apply(USArrests,2,mean)
##   Murder  Assault UrbanPop     Rape 
##    7.788  170.760   65.540   21.232
apply(USArrests,2,var)
##     Murder    Assault   UrbanPop       Rape 
##   18.97047 6945.16571  209.51878   87.72916
##发现均值和方差的差异较大，因此必须进行标准化
## scale(USArrests,center = T,scale = T)
##然后进行PCA分析，函数包含了标准化操作
pr.out<-prcomp(USArrests,scale=T)
names(pr.out)
## [1] "sdev"     "rotation" "center"   "scale"    "x"
##center和scale是标准化前的均值和标准差
##rotation包含了主成分载荷信息，列向量是主成分载荷向量
pr.out$rotation
##                 PC1        PC2        PC3         PC4
## Murder   -0.5358995  0.4181809 -0.3412327  0.64922780
## Assault  -0.5831836  0.1879856 -0.2681484 -0.74340748
## UrbanPop -0.2781909 -0.8728062 -0.3780158  0.13387773
## Rape     -0.5434321 -0.1673186  0.8177779  0.08902432
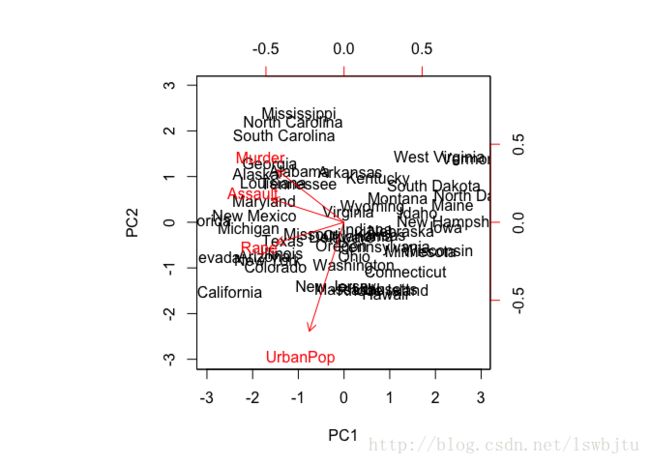
biplot(pr.out,scale=0) ##前两个主成分的双标图

##主成分的标准差
pr.out$sdev ##一般来说，第一主成分的方差>第二主成分的方差>.....
## [1] 1.5748783 0.9948694 0.5971291 0.4164494
pr.out$var<-pr.out$sdev^2
##计算每个主成分的方差解释比例
pve<-pr.out$var/sum(pr.out$var)
pve
## [1] 0.62006039 0.24744129 0.08914080 0.04335752
##绘制每个主成分的PVE和累积PVE图
par(mfrow=c(1,2))
plot(pve,xlab = "Principal Component",ylab="Proportion of Variance Explained",
     ylim=c(0,1),type='b')
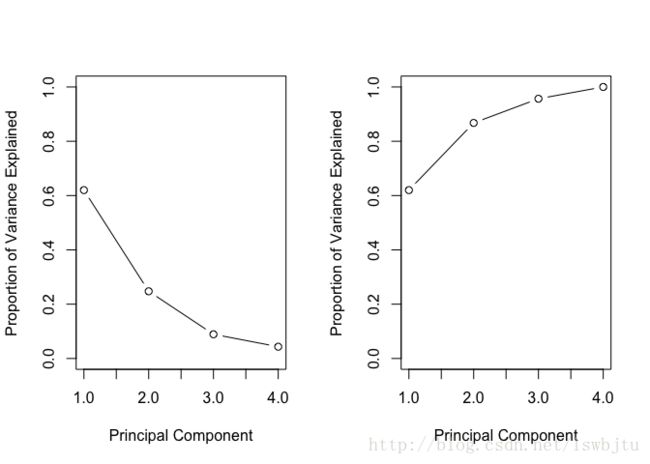
plot(cumsum(pve),xlab = "Principal Component",ylab="Proportion of Variance Explained",
     ylim=c(0,1),type='b')

PVE图和累积PVE图可以用于选择主成分，一般选取前几个能解释大部分数据方差的主成分。

三、判断主成分的个数

1.可根据上述提到的累积PVE图，解释大部分方差。

2.主成分对应于相关系数矩阵的特征值，第一主成分与最大特征值关联，第二主成分与第二大的特征值关联 - Kaiser-Harris准则：保留特征值大于1的主成分，特征值小于1的成分解释的方差更少。

• Cattell碎石检验：绘制了特征值与主成分数的图形，在图形变化最大处之上的主成分保留

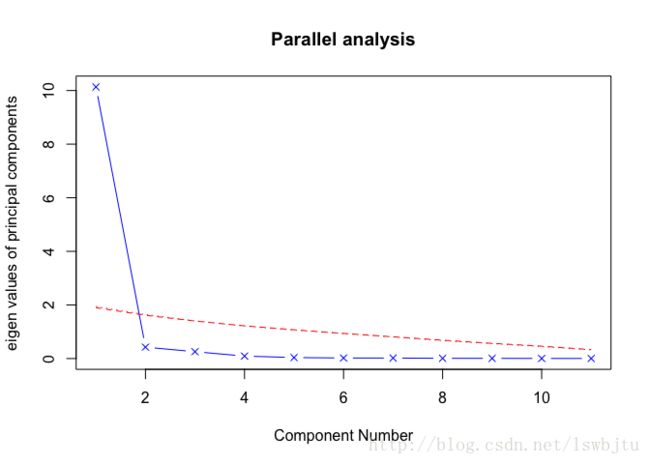
• 平行分析：用与初始矩阵大小相同的随机数矩阵，若基于真实数据的某个特征值大于一组随机数矩阵相应 的平均特征值，那么该主成分可以保留。

library(psych)
fa.parallel(USJudgeRatings[,-1],fa="pc",n.iter=100,show.legend=F,main = "Parallel analysis")

## Parallel analysis suggests that the number of factors =  NA  and the number of components =  1

四、提取主成分

principal(USJudgeRatings[,-1],nfactors = 1,scores = T)
## Principal Components Analysis
## Call: principal(r = USJudgeRatings[, -1], nfactors = 1, scores = T)
## Standardized loadings (pattern matrix) based upon correlation matrix
##       PC1   h2     u2 com
## INTG 0.92 0.84 0.1565   1
## DMNR 0.91 0.83 0.1663   1
## DILG 0.97 0.94 0.0613   1
## CFMG 0.96 0.93 0.0720   1
## DECI 0.96 0.92 0.0763   1
## PREP 0.98 0.97 0.0299   1
## FAMI 0.98 0.95 0.0469   1
## ORAL 1.00 0.99 0.0091   1
## WRIT 0.99 0.98 0.0196   1
## PHYS 0.89 0.80 0.2013   1
## RTEN 0.99 0.97 0.0275   1
## 
##                  PC1
## SS loadings    10.13
## Proportion Var  0.92
## 
## Mean item complexity =  1
## Test of the hypothesis that 1 component is sufficient.
## 
## The root mean square of the residuals (RMSR) is  0.04 
##  with the empirical chi square  6.21  with prob <  1 
## 
## Fit based upon off diagonal values = 1
## nfactors:设定主成分个数
## scores：是否计算主成分得分

计算结果中，h2指主成分对每个变量的解释比例，u2指无法被解释的比例，SS 表示主成分对应的特征值，Proportion 表示主成分解释比例

五、主成分旋转

• 正交旋转：选择的成分保持不相关
• 斜交旋转：选择的成分保持相关 正交旋转，方差极大旋转，对载荷矩阵的列进行去噪，使每个成分只由一组有限的变量来解释。

##varimax:方差极大旋转
data_pca<-principal(USJudgeRatings[,-1],nfactors = 2,rotate='varimax',scores=T)
data_pca
## Principal Components Analysis
## Call: principal(r = USJudgeRatings[, -1], nfactors = 2, rotate = "varimax", 
##     scores = T)
## Standardized loadings (pattern matrix) based upon correlation matrix
##       RC1  RC2   h2     u2 com
## INTG 0.48 0.87 0.98 0.0164 1.6
## DMNR 0.47 0.87 0.97 0.0252 1.6
## DILG 0.81 0.54 0.95 0.0531 1.7
## CFMG 0.88 0.45 0.97 0.0312 1.5
## DECI 0.89 0.43 0.97 0.0282 1.5
## PREP 0.82 0.56 0.98 0.0232 1.8
## FAMI 0.81 0.55 0.96 0.0405 1.8
## ORAL 0.77 0.63 0.99 0.0091 1.9
## WRIT 0.77 0.62 0.98 0.0196 1.9
## PHYS 0.79 0.44 0.82 0.1779 1.6
## RTEN 0.70 0.70 0.98 0.0176 2.0
## 
##                        RC1  RC2
## SS loadings           6.30 4.26
## Proportion Var        0.57 0.39
## Cumulative Var        0.57 0.96
## Proportion Explained  0.60 0.40
## Cumulative Proportion 0.60 1.00
## 
## Mean item complexity =  1.7
## Test of the hypothesis that 2 components are sufficient.
## 
## The root mean square of the residuals (RMSR) is  0.02 
##  with the empirical chi square  1.53  with prob <  1 
## 
## Fit based upon off diagonal values = 1

获得主成分与各个变量的线性关系：

data_pca$weights
##              RC1         RC2
## INTG -0.48346666  0.74273535
## DMNR -0.48569660  0.74465965
## DILG  0.20799349 -0.10532833
## CFMG  0.37290093 -0.31034542
## DECI  0.39824278 -0.34206511
## PREP  0.19639630 -0.08844609
## FAMI  0.19341796 -0.08612799
## ORAL  0.07139417  0.06794620
## WRIT  0.07630098  0.06104358
## PHYS  0.29502592 -0.22487622
## RTEN -0.07162767  0.24353657

获得主成分的得分：

data_pca$scores
##                         RC1          RC2
## AARONSON,L.H.   -0.43625484  0.244382210
## ALEXANDER,J.M.  -0.10942078  1.324198203
## ARMENTANO,A.J.  -0.13200175  0.275566691
## BERDON,R.I.      1.03630087  0.524734415
## BRACKEN,J.J.    -0.84161349 -2.393324391
## BURNS,E.B.       0.07016044  1.133641671
## CALLAHAN,R.J.    0.80342055  0.955949303
## COHEN,S.S.      -1.48721483 -2.158157424
## DALY,J.J.        0.78118367  0.862237453
## DANNEHY,J.F.     1.34837402 -1.144061632
## DEAN,H.H.       -0.22300367  0.106829116
## DEVITA,H.J.     -1.13307674  0.680899493
## DRISCOLL,P.J.   -1.67954055  1.743477389
## GRILLO,A.E.     -1.03431030 -0.333006989
## HADDEN,W.L.JR.   0.55568244 -0.013057617
## HAMILL,E.C.     -0.24589775  0.081800124
## HEALEY.A.H.     -1.11092595 -0.072503392
## HULL,T.C.        0.36760733 -0.813535607
## LEVINE,I.        0.26214560 -0.002514484
## LEVISTER,R.L.   -0.42930902 -1.642625753
## MARTIN,L.F.     -1.70399893  1.199710785
## MCGRATH,J.F.    -0.93021019 -0.407508501
## MIGNONE,A.F.    -3.02272761  0.563745360
## MISSAL,H.M.     -0.71555075  0.842676970
## MULVEY,H.M.      0.96871191  0.476402631
## NARUK,H.J.       1.43954883  0.492593338
## O'BRIEN,F.J.     0.05462851  0.681736508
## O'SULLIVAN,T.J.  0.59487618  0.998368712
## PASKEY,L.        1.03774800 -0.338111014
## RUBINOW,J.E.     0.94982286  1.212624991
## SADEN.G.A.       1.76584671 -1.637857192
## SATANIELLO,A.G.  0.20423752  0.019872042
## SHEA,D.M.        1.07210787 -0.036757710
## SHEA,J.F.JR.     0.76998366  0.844587964
## SIDOR,W.J.      -1.37809553 -1.724334530
## SPEZIALE,J.A.    0.78017665  0.048591613
## SPONZO,M.J.      0.26696254  0.271806601
## STAPLETON,J.F.   0.24752546  0.051941979
## TESTO,R.J.      -0.32808603 -0.645394531
## TIERNEY,W.L.JR.  0.81387101 -0.330270574
## WALL,R.A.        0.38346323 -1.766162327
## WRIGHT,D.B.     -0.13301770  0.895446778
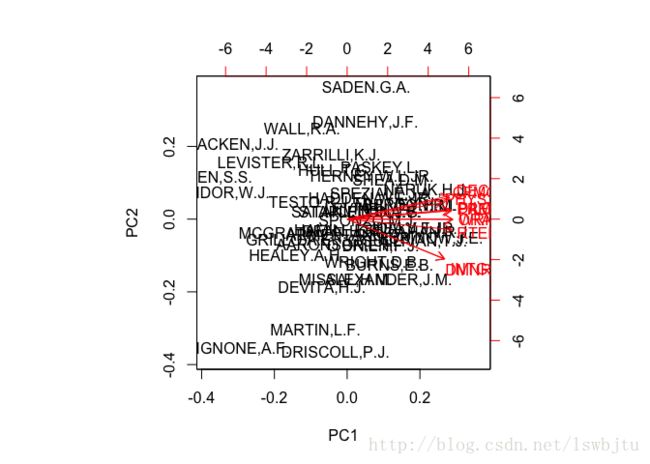
## ZARRILLI,K.J.    0.49987054 -1.074638671

获得主成分分析图

biplot(prcomp(USJudgeRatings[,-1],scale=T))

推广：在多重共线性存在时，线性回归的效果并不是很好，这时候可以考虑先用PCA降维，挑选出少量的主成分以后，将主成分作为自变量进行预测，此时得到的效果要更好。即避免了多重共线性，又有效的解释了自变量和因变量的关系。