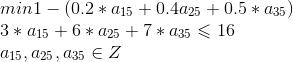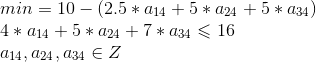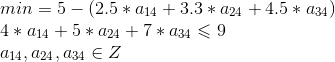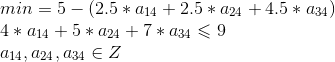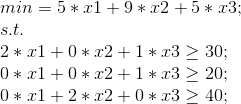运筹优化学习21：Java调用Cplex实现求解Cuting Stock Porblem的列生成算法详解

目录

1 CSP问题与模型

1.1 问题描述

1.2 模型构建

2 列生成方法理论

2.1 引子

2.2 单纯形法到列生成

2.3 subproblem

2.3.1 对偶理论

2.3.2 影子价格

2.4 小结

3 Cplex OPL演示列生成迭代过程

3.1 第一次迭代

3.2 第二次迭代

3.3 第三次迭代

3.4 最终RMP

4 多种长度木材的例子

4.1 问题说明

4.2 Cplex OPL求解

4.2.1 初始RMP

4.2.2 第一次进基离基

4.2.3 第二次进基离基

4.2.4 第三次进基离基

4.2.5 解的分析

4.2.6 总结

5 Java调用Cplex实现的列生成算法

5.1 遇到的问题及解决

5.1.1 运行步骤

5.1.2 JNI错误及处理办法

5.2 算例及运行

X 参考资料

---

1 CSP问题与模型

1.1 问题描述

我们有以下问题，原纸卷每个长为L=16m，顾客们分别需要25个3m长，20个6m长，18个7m长的纸卷。那么需要怎样切割才能使得浪费最小呢？

1.2 模型构建

假设有 n 中可行的裁切方案

参数	描述
	第j种裁切方案选择的个数
	第j种方案中类别i的个数

由此我们得到模型如下：

2 列生成方法理论

2.1 引子

列生成方法是求解大规模线性规划问题的有效方法，这里的大规模是指问题的约束数目有限但变量数目随着问题规模的膨胀而急速膨胀的线性规划问题。

我们刚才讨论的CSP就很好的满足了这一点：

顾客需求确定，约束个数就是确定的；但是有效的方案数目是不确定的

假定n=100时，变量数为100；当n=1,000,000,000时，变量数为1,000,000,000

2.2 单纯形法到列生成

我们都知道求解线性规划的最经典的方法是单纯形法，它是一种在解空间的顶点上迁移来找到问题最优解的算法；但是对于变量很多的LP时，我们遍历顶点的代价是很大的。但是有一点我们肯定知道，那就是我们的约束个数是等于基变量的个数的。另外i啊我们每一步的操作只会让一个非基变量进基。

为了更好的说明先澄清几个概念：

概念	解释	示例
master problem	原始的大规模线性规划问题
restricted master problem	变量数比原问题更少到约束不少的LP
subproblem	用来检查剩余变量的reduced cost

基于上面的解释和概念定义，我们就可以描述单纯形法到列生成的演变路径：

1. 将MP限制到一个变量更少的子问题RMP，使用单纯形法求解RMP的最优解
2. 使用subproblem去检验剩余变量的reduced cost是否小于0；若是，将与该变量相关的系数列加入到RMP中，返回第1步；否则，得到了原问题的最优解。

2.3 subproblem

这里终点讨论一下子问题，子问题的作用是为了检查剩余非基变量的reduced cost，确定它能否作为入基变量。

先来一张规范的单纯形表：

在单纯形法中，我们通过计算非基变量检验数 ，为负且最小的情况下的变量作为入基变量

在这个问题中，我们求解的关键是，它包含两重含义：

1. 通过求解RMP问题得到的影子价格（shadow price）。
2. 通过求解RMP对偶问题得到的对偶变量(dual variable)。

通俗的理解，影子价格是针对RMP本身而言的，而对偶变量是针对RMP的对偶问题而言的。

若对影子价格和对偶变量理论不熟悉，可前去阅读2.3.1和2.3.2的内容；否则我们继续

作为一个懒虫，我们肯定是咋简单咋来：

• 要想得到影子价格，我们就得解RMP，但是很不幸RMP有很多变量，单纯形法可能解不了；此路不通
• 对偶问题变量少啊，那我们当然选择从对偶变量下手

那就好办了，我们通过求RMP的对偶问题来求解，从而得到非基变量的检验数，然后建立以检验数最小为目标的subproblem，如果它的目标函数为负，说明这个列可以加入到RMP中；如果它非负，说明已经得到了最优解

2.3.1 对偶理论

对于每个线性规划问题都有一个对偶问题，得到了一个问题的解，另一个问题的解也就迎刃而解了。

再啰嗦一下：

1. 对偶问题的目标函数的系数是原问题约束的右端项
2. 对偶问题的系数矩阵是原问题系数矩阵的转置
3. 对偶问题的约束都是 ≤ ；原问题的约束都是 ≥
4. 对偶问题求最小则原问题求最大
5. 对偶问题的剩余变量和原问题的基变量共同构成了变量空间
6. 对偶问题研究的是资源的估价问题，原问题研究的是资源的最优分配问题

2.3.2 影子价格

对偶变量表示市场对单位第 i 种资源的估价，这种估价是由资源在生产过程发挥的作用决定的。

在资源最优利用条件下的估价，被我们称为该资源的影子价格；

下面是几点解释：

1. 也可认为是在最优条件下，增加每单位 i 资源，对目标函数的增量贡献值。
2. 当资源利用不充分时，他的影子价格为0；而影子价格不为0时，表示该资源已经耗尽
3. 结合检验数的计算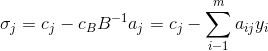，，前一项为产品 j 的产值，后一项为生产该产品消耗各资源的影子价格之和(隐含成本)。当产品产值大于资源隐含成本时，生成才有意义，所以检验数必须为非负

2.4 小结

列生成就是从一个变量较少的RMP开始，在得到RMP最优解后，利用其对偶变量建立起一个检验数最小化subproblem；若subproblem目标值为负，则增加新列到RMP中；如果subproblem目标值非负，则得到RMP的最优解。

所谓列生成，就是在每次迭代中添加一个列，直到无列可加时，得到的RMP的最优解就是原问题最优解。

列生成解决的是线性规划问题，如果要解决整数规划问题，还需要借助分支定界法、分支定价、分支切割等方法

3 Cplex OPL演示列生成迭代过程

3.1 第一次迭代

如果每个纸卷只裁切一个类别的纸卷，我们可以得到初始方案：

A = [5,0,0; 0,2,0; 0,0,2]

因此我们选择前三个方案，构建的RMP模型为：

Cplex OPL代码：

 dvar int+ y1; dvar int+ y2; dvar int+ y3;
 minimize y1 + y2 + y3;
 subject to{
5*y1 + 0*y2 + 0*y3 >= 25;
0*y1 + 2*y2 + 0*y3 >= 20;
0*y1 + 0*y2 + 2*y3 >= 18;
} 

得到结果为：Y = [5, 10, 9];

对偶变量为：

现在我们要加一列到RMP中，记为，计算其检验数：

我们便得到了一个子问题：

Cplex代码：

dvar int+ a14; dvar int+ a24; dvar int+ a34;
minimize 1 - (0.2*a14 + 0.5*a24 + 0.5*a34);
subject to{
3*a14 + 6*a24 + 7*a34 <= 16;
}

得到，ruduce cost的取值为负数，因此加入

3.2 第二次迭代

得到新的RMP：

 dvar int+ y1; dvar int+ y2; dvar int+ y3; dvar int+ y4;
 minimize y1 + y2 + y3 + y4;
 subject to{
5*y1 + 0*y2 + 0*y3 + 1*y4 >= 25;
0*y1 + 2*y2 + 0*y3 + 2*y4>= 20;
0*y1 + 0*y2 + 2*y3 + 0*y4>= 18;
}

得到结果为：Y = [3,0,9,10];

对偶变量为：

现在我们要加一列到RMP中，记为，计算其检验数：

得到子问题：

得到，ruduce cost的取值为负数，因此加入

3.3 第三次迭代

 dvar int+ y1; dvar int+ y2; dvar int+ y3; dvar int+ y4;dvar int+ y5;
 minimize y1 + y2 + y3 + y4 + y5;
 subject to{
5*y1 + 0*y2 + 0*y3 + 1*y4 + 1*y5>= 25;
0*y1 + 2*y2 + 0*y3 + 2*y4 + 1*y5 >= 20;
0*y1 + 0*y2 + 2*y3 + 0*y4 + 1*y5>= 18;
}

得到结果为：Y = [2,0,0,1,18];

对偶变量为：

现在我们要加一列到RMP中，记为，计算其检验数：

得到子问题：

得到，ruduce cost的取值为0，因此不加入

3.4 最终RMP

令上述模型中的决策变量都取整数，得到的Cplex的最优方案组合为[2,0,0,1,18]，最优值为21

对应到实际问题就是，2个卷切5个3米的；1个卷1个3米和2个6米；18个卷切1个3米、1个6米和1个7米

最终我们得到了29个3米的，20个6米的，18个7米的；总共切了21个卷，浪费21*16 - (25*3 + 6*20 + 7*18)=15米

4 多种长度木材的例子

4.1 问题说明

有三种长度为9,14,16的木材，成本价分别为5,9,10，需要切割长度为4的成品 30个；长度为5的成品20个；长度为7的成品40个，求解切割方案，使得总体成本价最低。

构建的模型：

参数	描述
	第j种切割方案
	第j种切割方案的成本
	第j种切割方案得到i型木材的数目

模型：

找初始方案： 

4.2 Cplex OPL求解

4.2.1 初始RMP

Cplex求解：

dvar int+ x1; dvar int+ x2; dvar int+ x3;
minimize 5*x1 + 5*x2 + 5*x3; 
subject to{
2*x1 + 0*x2 + 0*x3 >= 30;
0*x1 + 1*x2 + 0*x3 >= 20;
0*x1 + 0*x2 + 1*x3 >= 40;
}

决策变量X = [15,20,40]; 对偶变量：[2.5,5,5]；最优值375

构建新的列：

构建subproblem时，我们再求时，发现 有三个，那么我们就需要构建三个子问题，然后得到其中的最大的

问题	subproblem 1 --》 9米，5元	subproblem 2 --》 14米，9元	subproblem 3 --》 16米，10元
模型
Cplex	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 5 - (2.5*a14 + 5*a24 + 5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 9; }	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 9 - (2.5*a14 + 5*a24 + 5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 14; }	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 10 - (2.5*a14 + 5*a24 + 5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 16; }
	[1,1,0]	[1,2,0]	[0,3,0]
	-2.5	-3.5	-5.0

检验数相同，我们选择成本更低的方案，因此我们新增加的列是[0,3,0]

4.2.2 第一次进基离基

Cplex求解：

dvar int+ x1; dvar int+ x2; dvar int+ x3; dvar int+ x4;
minimize 5*x1 + 5*x2 + 5*x3 + 10*x4; 
subject to{
2*x1 + 0*x2 + 0*x3 + 0*x4 >= 30;
0*x1 + 1*x2 + 0*x3 + 3*x4 >= 20;
0*x1 + 0*x2 + 1*x3 + 0*x4 >= 40;
}

X = [15, 0, 40, 6.7]; 目标值341.67；对偶变量：[2.5, 3.3, 5]

对应最优整数解， X = [15, 0, 40, 7]; 目标345

可知，变量  应该离基，构建新的列：

问题	subproblem 1 --》 9米，5元	subproblem 2 --》 14米，9元	subproblem 3 --》 16米，10元
模型
Cplex	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 5 - (2.5*a14 + 3.3*a24 + 5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 9; }	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 9 - (2.5*a14 + 3.3*a24 + 5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 14; }	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 10 - (2.5*a14 + 3.3*a24 + 5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 16; }
	[1,1,0]	[0,0,2]	[1,1,1]
	-0.8	-1	-0.8

添加列[0,0,2],离基列[0,1,0]

4.2.3 第二次进基离基

为便于表述，我们将x2直接换掉：

Cplex求解：

dvar int+ x1; dvar int+ x2; dvar int+ x3; dvar int+ x4;
minimize 5*x1 + 9*x2 + 5*x3 + 10*x4; 
subject to{
2*x1 + 0*x2 + 0*x3 + 0*x4 >= 30;
0*x1 + 0*x2 + 0*x3 + 3*x4 >= 20;
0*x1 + 2*x2 + 1*x3 + 0*x4 >= 40;
}

X = [15,20,0,6.7]; 目标值321.67；对偶变量：[2.5,3.3,4.5]

对应整数解为X = [15, 20, 0, 7];目标值325

 应该离基，构建新列

问题	subproblem 1 --》 9米，5元	subproblem 2 --》 14米，9元	subproblem 3 --》 16米，10元
模型
Cplex	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 5 - (2.5*a14 + 3.3*a24 + 4.5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 9; }	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 9 - (2.5*a14 + 3.3*a24 + 4.5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 14; }	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 10 - (2.5*a14 + 3.3*a24 + 4.5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 16; }
	[1,1,0]	[1, 2, 0]	[1,1,1]
	-0.8	-0.1	-0.3

进基列[1, 1, 0];离基列[0, 0, 1]

4.2.4 第三次进基离基

直接换掉,

Cplex求解：

dvar int+ x1; dvar int+ x2; dvar int+ x3; dvar int+ x4;
minimize 5*x1 + 9*x2 + 5*x3 + 10*x4; 
subject to{
2*x1 + 0*x2 + 1*x3 + 0*x4 >= 30;
0*x1 + 0*x2 + 1*x3 + 3*x4 >= 20;
0*x1 + 2*x2 + 0*x3 + 0*x4 >= 40;
}

X = [5, 20, 20, 0]; 目标值305；对偶变量：[2.5,2.5,4.5]

 应该离基，构建新列

问题	subproblem 1 --》 9米，5元	subproblem 2 --》 14米，9元	subproblem 3 --》 16米，10元
模型
Cplex	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 5 - (2.5*a14 + 2.5*a24 + 4.5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 9; }	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 9 - (2.5*a14 + 2.5*a24 + 4.5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 14; }	dvar int+ a14; dvar int+ a24; dvar int+ a34; minimize 10 - (2.5*a14 + 2.5*a24 + 4.5*a34); subject to{ 4*a14 + 5*a24 + 7*a34 <= 16; }
	[1,1,0]	[0,0,2]	[4,0,0]
	0	0	0

三个检验数都为0，我们完美的找到了问题的最优解，而且还是整数解。

4.2.5 解的分析

有三种长度为9,14,16的木材，成本价分别为5,9,10，需要切割长度为4的成品 30个；长度为5的成品20个；长度为7的成品40个，求解切割方案，使得总体成本价最低。

X = [5, 20, 20]; 目标值305

5个[2,0,0]的方案，20个[0,0,2]的方案，20个[1,1,0]的方案

方案为：9米的木材切成两个4米，方案使用5次； 9米木材切成1个4米、1个5米的方案使用20次； 14米木材切成2个7米的方案使用20次

该方案浪费木料为：5 * 1 + 20*0 + 20*2 = 45米；一共使用了45根木材，25根14米木材，没有使用16米的木材。

4.2.6 总结

这一节我们计算了3种不同成本的木材型号和3种需求的CSP问题的求解实例验证，做如下小结：

1. 由于我们只有3个约束，要先选择三个可行的裁切方案作为初始裁切组合
2. 我们构建了3种木材类型的subproblem，subprobelm的约束根据可用的木材型号设置
3. 进基变量是subproblem目标负最小值列；离基变量为决策变量取值为0的列；一进一出，始终保持模型只处理4个变量
4. RMP的每次优化都会得到新的决策变量及其对偶变量的取值
5. 对偶变量发生变化时，每个subproblem只需更新他的目标函数即可，约束不用动
6. 终止的条件是所有的subproblem的最优目标值非负

5 Java调用Cplex实现的列生成算法

代码请关注文末公众号回复：java-cplex-CG-CSP

5.1 遇到的问题及解决

5.1.1 运行步骤

1. 导入Java工程：File --> import --> General --> Existing Projects into Workspace --> Next --> Select toot directory后输入工程父目录，下边勾选Copy projects into workspace --> Fnished
2. 运行工程：右键点击src --> cut --> CutStock.java，点击Run as --> 1 Java Application；此处弹出运行错误，以后处理

5.1.2 JNI错误及处理办法

1) 错误截图：

2) 原因：这个错误是因为项目的依赖库不对，需要你重新配置一下

3) 解决方案

该项目的 Build Path ， 在Libraries 中看到如下内容：

有两个路径缺失，我们要做的就是把这个路径删除，替换为我们自己

处理方式：

1. 选中第一行的cplex.jar，点击右侧的Remove；再点击Add External JARS ...，找到自己的cplex.jar，把它加进来
2. net.mindview.jar包，是java编程思想第四版中需要使用net.mindview.util包，下载地址， 提取码: a25m；下载之后，加载方式与 1 一致
3. 配置Java环境：Add Library.. -> JRE System Library -> Execution environment:JavaSE-1.8

5.2 算例及运行

数据	17.0 3.0 5.0 9.0  25.0 20.0 15.0
结果	Best integer solution uses 19.0 rolls   Cut0 = 0.0   Cut1 = 1.0   Cut2 = 0.0   Cut3 = 15.0   Cut4 = 3.0 Solution status: Optimal

X 参考资料

1. 干货 | 10分钟带你彻底了解column generation（列生成）算法的原理附java代码

2. 2018新java编程思想第四版中net.mindview.util包下载

3. 运筹优化学习09：一个示例带你入门如何使用C++、C#、Java、Python、Matlab调用Cplex

4. 运筹学教学|列生成（Column Generation）算法（附代码及详细注释）

5. 对 cplex/gurobi MPS/LP文件格式的理解​​​​​​​