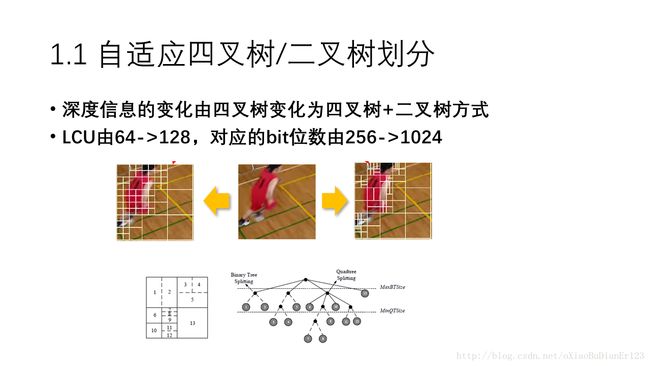
H.266深度信息划分(亮度/色度)
接下来准备针对代码的实现进行一些简要的说明。(其实我已经不做这个方向了,不过还是有一些思路,针对如何通过深度学习优化H266的编码过程,可以参考一下pix2pix,另外,对于这种QTBT的划分方式,在地图搜索里面也可以借鉴使用,例如根据中心点,搜索周围的候选,然后进一步所辖范围,最终达到一个完美的区域候选等。虽然已经不做这个内容,不过学习的过程在于迁移,一个方向的学习迁移到另外的方法,会得到不一样的体验)
-------
首先我们需要去H266的源代码获取两个信息,一个是LCU QT划分的模型,另外一个是LCU BT划分的模型,之后保存为文件之后,在mathlab里面,通过LCU_View(YUV_FileName, LCU_QT_FileName,~,Fid_LCU_BT_Split, Width, Height, NumFrame)的函数,完成划分。下面的是LCU_View(YUV_FileName, LCU_QT_FileName,~,Fid_LCU_BT_Split, Width, Height, NumFrame)函数的具体实现,其实就是根据数值代表的含义,进行递归操作。代码具体有没有bug我不清楚。。。
function LCU_View(YUV_FileName, LCU_QT_FileName,~,Fid_LCU_BT_Split, Width, Height, NumFrame)
clc;
%% setting parameter
LCU_Size = 128;
MaxNumPartition = 1024;
NumLCU_Row = floor( (Width + LCU_Size-1) / LCU_Size ); % the number of LCU in a row
NumLCU_Col = floor( (Height+ LCU_Size-1) / LCU_Size ); % the number of LUC in a column
Fid_YUV = fopen(YUV_FileName,'rb');
Fid_LCU_QT = fopen(LCU_QT_FileName,'rb');
Fid_LCU_BT_S = fopen(Fid_LCU_BT_Split,'rb');
for uiFrame = 1 : NumFrame
%% read data from files
ImgData = fread(Fid_YUV, [Width, Height], 'uint8'); % image data Y
% ImgData_U = fread(Fid_YUV ,[Width/2, Height/2], 'uint8'); % image data U
% ImgData_V = fread(Fid_YUV ,[Width/2, Height/2], 'uint8'); % image data V
ImgData = ImgData';
QTLCUData = fread(Fid_LCU_QT, [NumLCU_Row*NumLCU_Col*MaxNumPartition, 1], 'uint8'); % LCU data
BTSplitMode = fread(Fid_LCU_BT_S, [NumLCU_Row*NumLCU_Col*MaxNumPartition, 1], 'uint8');
BTSplitMode = bitand(BTSplitMode,63);
%% draw LCU lines
figure; imshow(ImgData,[])
for i = 1 : Width/LCU_Size
line([i*LCU_Size, i*LCU_Size], [1 Height],'Color', 'w','LineWidth',1)
end
for i = 1 : Height/LCU_Size
line([1 Width], [i*LCU_Size, i*LCU_Size],'Color', 'w','LineWidth',1)
end
for i = 1 : NumLCU_Col
for j = 1 : NumLCU_Row
Idx = (i-1) * NumLCU_Row + j;
uiPelX = (j-1) * LCU_Size + 1;
uiPelY = (i-1) * LCU_Size + 1;
QTLCUData_Blk = QTLCUData( (Idx-1)*MaxNumPartition + 1 : (Idx)*MaxNumPartition);
BTSplitMode_Blk = BTSplitMode( (Idx-1)*MaxNumPartition + 1 : (Idx)*MaxNumPartition);
DrawCUDepthLine(QTLCUData_Blk,BTSplitMode_Blk,uiPelX, uiPelY, LCU_Size, LCU_Size, MaxNumPartition);
end
end
end
fclose(Fid_YUV);
fclose(Fid_LCU_QT);
fclose(Fid_LCU_BT_S);
function DrawBTCUDepthLine(uiPelX, uiPelY, uiSize_X, uiSize_Y, uiNumPartition , flag, is_skip_array)
% 针对 is_skip_array 和 flag 信息进行判断
if flag == 0
return;
elseif flag == 1
% 水平分割
line([uiPelX, uiPelX + uiSize_X], [uiPelY + uiSize_Y/2, uiPelY + uiSize_Y/2], 'Color', 'g');
uiNextSize_X = uiSize_X;
uiNextSize_Y = uiSize_Y / 2;
uiNumPartitionNext = uiNumPartition/2;
for iAbsPartY = 1 : 2
for iAbsPartX= 1 : 1
iAbsPartIndex = (iAbsPartY-1);
iNextDepth_BT = is_skip_array(iAbsPartIndex * uiNumPartitionNext + 1 : (iAbsPartIndex+1) *uiNumPartitionNext, 1);
uiNextPelX = uiPelX + (iAbsPartX-1) * uiNextSize_X;
uiNextPelY = uiPelY + (iAbsPartY-1) * uiNextSize_Y;
bin_first = bitand(iNextDepth_BT,3);
if length(unique(bin_first)) == 1
skip_mode_flag = unique(bin_first);
is_skipe = bitshift(iNextDepth_BT,-2);
DrawBTCUDepthLine(uiNextPelX, uiNextPelY, uiNextSize_X, uiNextSize_Y, uiNumPartitionNext, skip_mode_flag, is_skipe)
else
% disp('测试')
% binarry_bin_1 = bin_first(1:length(bin_first)/2,:);
%
% if unique(binarry_bin_1) == 0
%
% elseif unique(binarry_bin_1) == 1
% line([uiPelX + uiSize_X/2, uiPelX + uiSize_X], [uiPelY + uiSize_Y/4, uiPelY + uiSize_Y/4], 'Color', 'r');
% elseif unique(binarry_bin_1) == 2
% line([uiPelX + uiSize_X/4, uiPelX + uiSize_X/4], [uiPelY, uiPelY + uiSize_Y], 'Color', 'r');
% end
%
% disp(binarry_bin_1')
% binarry_bin_2 = bin_first(length(bin_first)/2+1:length(bin_first),:);
%
% if unique(binarry_bin_2) == 0
%
% elseif unique(binarry_bin_2) == 1
% line([uiPelX+ uiSize_X/2, uiPelX + uiSize_X], [uiPelY + 3*uiSize_Y/4, uiPelY + 3*uiSize_Y/4], 'Color', 'r');
% elseif unique(binarry_bin_2) == 2
% line([uiPelX + 3*uiSize_X/4, uiPelX + 3*uiSize_X/4], [uiPelY, uiPelY + uiSize_Y], 'Color', 'r');
% end
%
% disp(iNextDepth_BT')
% DrawBTCUDepthLine(uiNextPelX, uiNextPelY, uiNextSize_X, uiNextSize_Y, uiNumPartitionNext, skip_mode_flag, is_skipe)
% disp('不规则')
end
end
end
elseif flag == 2
% 垂直分割
line([uiPelX + uiSize_X/2, uiPelX + uiSize_X/2], [uiPelY, uiPelY + uiSize_Y], 'Color', 'y');
uiNextSize_X = uiSize_X/2 ;
uiNextSize_Y = uiSize_Y ;
uiNumPartitionNext = uiNumPartition/2;
for iAbsPartY = 1 : 1
for iAbsPartX= 1 : 2
iAbsPartIndex = (iAbsPartX-1) ;
iNextDepth_BT = is_skip_array(iAbsPartIndex * uiNumPartitionNext + 1 : (iAbsPartIndex+1) *uiNumPartitionNext, 1);
uiNextPelX = uiPelX + (iAbsPartX-1) * uiNextSize_X;
uiNextPelY = uiPelY + (iAbsPartY-1) * uiNextSize_Y;
bin_first = bitand(iNextDepth_BT,3);
if length(unique(bin_first)) == 1
skip_mode_flag = unique(bin_first);
is_skipe = bitshift(iNextDepth_BT,-2);
DrawBTCUDepthLine(uiNextPelX, uiNextPelY, uiNextSize_X, uiNextSize_Y, uiNumPartitionNext, skip_mode_flag, is_skipe)
else
disp('zhangshan')
binarry_bin_1 = bin_first(1:length(bin_first)/2,:);
if unique(binarry_bin_1) == 0
elseif unique(binarry_bin_1) == 1
% line([uiPelX + uiSize_X/2, uiPelX + uiSize_X], [uiPelY + uiSize_Y/4, uiPelY + uiSize_Y/4], 'Color', 'r');
elseif unique(binarry_bin_1) == 2
is_skipe = bitshift(binarry_bin_1,-2);
DrawBTCUDepthLine(uiPelX/2, uiPelY/2, uiSize_X/2, uiSize_Y/2, uiNumPartition/2 , 2, is_skipe)
% line([uiPelX + uiSize_X/4, uiPelX + uiSize_X/4], [uiPelY, uiPelY + uiSize_Y], 'Color', 'r');
end
disp(binarry_bin_1')
binarry_bin_2 = bin_first(length(bin_first)/2+1:length(bin_first),:);
if unique(binarry_bin_2) == 0
elseif unique(binarry_bin_2) == 1
line([uiPelX+ uiSize_X/2, uiPelX + uiSize_X], [uiPelY + 3*uiSize_Y/4, uiPelY + 3*uiSize_Y/4], 'Color', 'r');
elseif unique(binarry_bin_2) == 2
line([uiPelX + 3*uiSize_X/4, uiPelX + 3*uiSize_X/4], [uiPelY, uiPelY + uiSize_Y], 'Color', 'r');
end
end
end
end
end
% 四叉树划分模块
function DrawCUDepthLine(DepthCTU, BTSplitMode_Blk ,uiPelX, uiPelY, uiSize_X, uiSize_Y, uiNumPartition)
% 四叉树分割方式
uiDepth = DepthCTU(1,1);
DepthCTU = DepthCTU -1;
if uiDepth > 0
line([uiPelX + uiSize_X/2, uiPelX + uiSize_X/2], [uiPelY, uiPelY + uiSize_Y], 'Color', 'b');
line([uiPelX, uiPelX + uiSize_X], [uiPelY + uiSize_Y/2, uiPelY + uiSize_Y/2], 'Color', 'b');
uiNextSize_X = uiSize_X /2;
uiNextSize_Y = uiSize_Y /2;
uiNumPartitionNext = uiNumPartition/4;
for iAbsPartY = 1 : 2
for iAbsPartX= 1 : 2
iAbsPartIndex = (iAbsPartY-1) * 2 + (iAbsPartX-1);
iNextDepth = DepthCTU(iAbsPartIndex * uiNumPartitionNext + 1 : (iAbsPartIndex+1) * uiNumPartitionNext, 1);
% 根据四叉树分割二叉树,因为二叉树基于四叉树分割后进行二次分割
iNextDepth_BT_S = BTSplitMode_Blk(iAbsPartIndex * uiNumPartitionNext + 1 : (iAbsPartIndex+1) *uiNumPartitionNext, 1);
uiNextPelX = uiPelX + (iAbsPartX-1) * uiNextSize_X;
uiNextPelY = uiPelY + (iAbsPartY-1) * uiNextSize_Y;
DrawCUDepthLine(iNextDepth,iNextDepth_BT_S, uiNextPelX, uiNextPelY, uiNextSize_X, uiNextSize_Y, uiNumPartitionNext);
end
end
else
% 第一次分割,首先判断每个部分,含有的数字个数,若只含有一个,则判断其后两位的值
bin_first = bitand(BTSplitMode_Blk,3);
if length(unique(bin_first)) == 1
skip_mode_flag = unique(bin_first);
is_skipe = bitshift(BTSplitMode_Blk,-2);
DrawBTCUDepthLine(uiPelX, uiPelY, uiSize_X, uiSize_Y, uiNumPartition ,skip_mode_flag,is_skipe)
else
disp('第一次二叉树划分bug')
end
end获取QT 和 BT的两个函数在PPT里面已经介绍,可以直接找到这两个函数,然后在中间加入
DepthInfo.open("BestDepth.txt", ios::app);
for(UInt iPartitionNum = 0; iPartitionNum < DepthCU->getTotalNumPart(); iPartitionNum++)
{
DepthInfo << DepthCU->getDepth()[iPartitionNum];
}
DepthInfo.close();具体代码在HEVC中的样子,参考这篇文章:https://blog.csdn.net/oXiaoBuDianEr123/article/details/78903438 在VS里面搜索一下对一个函数,分别把信息存入两个文件就可以。