EMR: To Learn or Not to Learn: Visual Localization from Essential Matrices && 2020论文笔记

---

通讯作者： Laura Leal-Taix ́e

第一作者：Qunjie Zhou

研究机构：慕尼黑工业大学,查尔默斯理工大学,微软

EMR证明了估计本质矩阵是比直接预测场景坐标更好的选择。理论上来说，相对位姿回归相比于绝对位姿回归应当有更好的跨场景泛化性，但是实验结果证明并非如此。作者通过实验探究发现，基于深度学习的场景坐标回归方法之所以泛化性差是因为位姿回归层输入的的高层级特征损失了定位精度，不利于精确的定位。

论文解决的问题

本文提出了基于传统特征方法进行相对位姿定位的框架，并达到了SOTA。在此基础上，通过将不同组件换为CNN模型进行分析， 探究了基于深度学习的相对位姿回归方法的性能低于SOTA的原因，然后对未来的工作提出了建议和展望。

现有方法的不足 & 本文贡献

现有的相机重定位SOTA框架均基于3D几何信息。几何信息要么是显式的形式（a 3D model,point-based or SFM model）要么是隐式的包含在CNN模型的权重中。这两种表示方式在不同场景下均需要重新训练，极大地限制了定位框架、模型的泛化能力。

相比于基于3D几何信息的方法，基于相对位姿估计的方法不依赖于场景坐标，具有简单灵活的特性，易于泛化到新的场景中。但是，现有的基于相对位姿估计的工作相比于SOTA其精度均存在一定程度的劣势。

本文工作：

• 提出了基于SIFT特征匹配的经典方法，基于CNN回归的方法，基于CNN学习特征进行匹配的经典方法，对比了三者精度，分析的基于深度学习的位姿回归方法精度不足的原因。

相关工作

1.基于特征匹配的定位方法

A.直接法（或取绝对位姿）

通过比对从查询图像提取的描述子 和 3D模型中的特征点直接进行匹配，精确但是算力、内存消耗大，在大场景中扩展性有限，且需要预先建好的3D模型。

B.间接法（获取相对位姿，计算得到绝对位姿）

首先进行图像检索，在数据库中通过比对图像描述子找到与查询图像最接近的prior images，然后可以通过这些prior images在线生成局部SFM model进行特征比对，或者对 从查询图像到prior images的位置 进行三角化，通过RANSAC或者其变种实现相对位姿的确定。由于prior images的绝对位姿已知，因此根据相对位姿可以确定查询图像的绝对位姿。

2.基于局部学习的方法

深度学习对基于检索的方法产生了很大的帮助（如NetVLAD）。对于基于3D几何结构的方法，已经产生了一些工作如DSAC，DSAC++等，直接学习2D-3D的匹配关系。

这种方法主要的缺点除了大场景中的可扩展性不足之外，还有更换场景时需要重新训练，而训练时间一般是较长的（1-7天）。

3.绝对位姿估计（APE， absolute pose estimation）

这种方法 使用深度神经网络的分类或者回归方法 学习整个定位pipeline。通常训练数据只需要图像以及对应的相机位姿真值。使用2D-3D匹配的信息作为损失函数的一部分将有助于提升精度（PoseNet2）。同样，训练的模型是只针对特定场景的，更换场景时需要重新训练。使用序列图像作为位姿回归的输入数据相比于输入单张图像有很大的提升（VLocNet++）。

4.相对位姿估计（RPE，relative pose estimation）

相比于绝对位姿估计只适用于特定场景，预测两张图像之间的相对位姿理论上能够提升模型的跨场景泛化性。NNnet使用了图像检索+CNN回归相对位姿的结构，在最后的RANSAC loop中使用三角定位得到查询图像的绝对位姿。其损失函数包括平移损失和旋转损失两部分，通过超参数$\beta$相加。由于在不同的场景中平移误差和旋转误差相差较大，因此超参数$\beta$在每个新的场景中都需要调整。

基于此，本文证明了相比于回归相对位姿，回归本质矩阵是一种更好的选择。同时由于一个本质矩阵可以解算出四个位姿，作者提出了一种新的RANSAC机制来解决位姿歧义问题。最后通过将部分组件换为数据驱动的部件（基于学习的方法），分析了相机定位pipeline中学习失败的地方，证明了学习整个定位pipeline并不是最精确的方法。

论文方法介绍

分为三个步骤：

1. 图像检索，得到接近查询图像的一系列近邻图像
2. 对每一个近邻图像，计算与查询图像之间的本质矩阵。
3. 根据本质矩阵与近邻图像的绝对位姿，求得查询图像的绝对位姿

使用本质矩阵而不是相对位姿的原因：

预测相对位姿时，损失函数中有一个需要根据场景调整调整的超参数，而在某一个场景中合适的超参数值只能通过grid search求得，限制定位pipeline 的跨场景泛化性

而预测本质矩阵则将场景解耦，无需调整参数，并且能够提升定位精度。

尽管使用本质矩阵将会带来解算位姿歧义的问题，本文提出新的RANSAC机制解决了这个问题。

Notation

图像：$I$

相机绝对位姿：$(R_I,t_I)$,实际上是通过四元数q来表示旋转矩阵R的

全局坐标：$x$

相机坐标：$R_{I}x+t_I$

相机中心的全局坐标：$c_I=-R_I^T{t}_I$

1.图像检索

使用4096维的DenseVLAD图像描述子来进行检索。相比其他描述子，DenseVLAD 描述子泛化性更好。

仅仅选择top-k近邻的图像并不能够保证很好的精度。好的近邻图像应当满足：

1. 与查询图像有足够的视觉重叠
2. 查询图像到近邻图像之间的夹角应当尽量大，以方便三角定位。考虑极端情况，沿直线行驶的骑车采集到的图像检索得到的近邻图像不能用于三角定位。

因此采用迭代的方法选择一定距离的检索图像最后得到近邻图像。

最后得到的检索-近邻图像对则用于计算本质矩阵。

2.相对位姿估计

对每一对查询-近邻图像，计算得到一个本质矩阵E。根据E可以解算出四个位姿（R,t）（R,-t）（R’,t）（R’,-t），其中R‘是R旋转180度的矩阵。

传统方法一般会使用基于特征匹配的cheirality test确定正确的解，但是本文回归相对位姿的方法不提供这种匹配。

因此作者使用了triangulation的方法：已知相对位姿和近邻图像的绝对位姿，可以消除平移量的歧义，只需要确定旋转量就可以了。这样将歧义的候选位姿降为了2个，即两个旋转矩阵，R 和R’。

记查询图像为$I_q$,

两个近邻图像$I_i,I_j$的绝对位姿已知：$R_{I_i},R_{I_j}$，相对位姿：$R_i,t_i;R_j,t_j$

根据之前的三角定位，候选的相对位姿（仅考虑旋转）有四个：$R_i,R_j,R_i^{\prime },R_j^{\prime }$

对应的四个绝对位姿：$R_i{R}_{I_i},R_i^{\prime }{R}_{I_i},R_j{R}_{I_j},R_j^{\prime }{R}_{I_j}$

如果计算正确的话这四个绝对位姿中应该有两个是相同的。由此根据两个近邻图像确定出一个绝对位姿假设。

3.绝对位姿计算（via normal RANSAC）

查询图像的坐标可以根据两条射线的交点：
$$\begin{gathered} c_{I_i}+{\lambda }_i{R}_{I_i}^T{R}_i{t}_i \\ {c}_{I_j}+{\lambda }_j{R}_{I_j}^T{R}_j{t}_j \end{gathered}$$
来确定。只有当图像$I_i,I_j,I_q$的光心在一条交点上时，该方法无法进行定位。

NORMAL RANSAC:

在每个迭代步骤：

1. 使用任意两个图像对得到一个绝对位姿的假设$(R_{I_q},t_{I_q})$

2. 统计所有图像对中 该位姿假设的inliers:

   对任一图像对$(I_q,I_k)$,有四个可能的位姿，找到能使$R_k{R}_{I_k}$最接近$R_{I_q}$的$R_k$,

   由姿态$(R_{I_q},t_{I_q})$预测的从I_q到I_k的相对平移为：$t_{pred}=R_{I_k}(c_{I_q}-c_{I_k})$

   一致性衡量：
   $$\alpha =co{s}^{-1}(\frac{t_k^T{t}_{pred}}{(||t_k|{|}_2||t_{pred}|{|}_2)}$$
   若夹角小于阈值，则计为inlier

选择inlier最多的假设作为最终的输出。

4.本质矩阵估计

作者设计了三种架构来进行本质矩阵估计：基于手工特征的方法和基于学习的方法，以及二者混合的方法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-trFuahw4-1592899316595)(https://i.loli.net/2020/06/23/t4hy8BZxdQsTXGV.png)]

A. Feature-based: SIFT + 5-Point Solver

这个作为baseline.

在图像检索阶段使用基于SIFT的2D-2D匹配方法找到近邻候选图像，通过在RANSAC loop中的5-point solver这些匹配被用于估计本质矩阵。该方法不需要3D model

B. Learning-based: Direct Regression via EssNet

使用孪生ResNet34作为backbone, 之后加入了一个类似于传统方法的特征匹配的步骤。

特征匹配设计了两个变种：

1. 直接使用EssNet作为固定的简单匹配层。（本质上是来自两个图像的特征图之间的矩阵点乘）
2. 可学习的近邻关系匹配层 (NC-EssNet)，（匹配时强制满足几何一致性）

两个匹配版本都将ResNet生成的两个特征图组合成一个单一的特征张量，可以看作是一个匹配的得分图。

这个得分图被输入到回归层中输出一个9维的本质矩阵。（将前两个奇异值替换为其平均值，并将最小奇异值设置为0）

损失函数：$Loss(E^{\ast },E)=\Vert e-e^{\ast }|{|}_2$,e是本质矩阵向量化后的9维向量

C. Hybrid: Learnable Matching + 5-Point Solver

通过神经网络进行特征提取和匹配得到一组2D-2D的匹配，使用RANSAC loop中的5-point 求解算法得到本质矩阵。

从结构上看，相当于NC-EssNet去掉了回归层的版本。

实验内容以及分析

在每个数据集上，所有的场景图片一起训练，测试时不论什么场景均使用同一个网络。

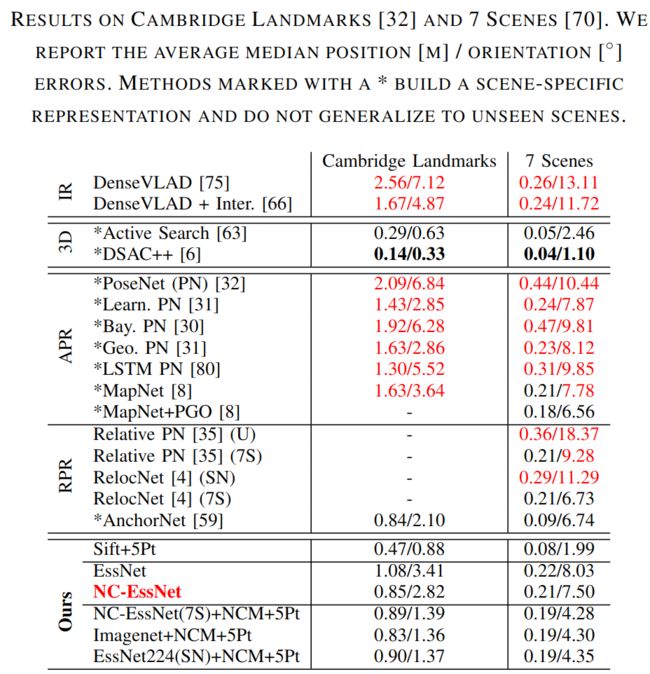
带* 的表示不能够在新的场景中泛化的方法。IR 表示基于图像检索的方法。

• 基于传统手工特征的方法:

  SIFT+5P：使用COLMAP和opencv 中的5-Point RANSAC进行特征提取和匹配。可见其精度均高于IR、APR、RPR的方法。对于基于3D结构的方法，虽然精度稍差，但是不需要特定场景的3D模型，且泛化性强。此外，DSAC++ 需要2+days的训练时间，而SIFT+5P的方法轻量且不需要训练。

本文另一个目的是分析RPR方法精度不如基于3D结构方法的原因。

• 图表中精度低于NC-EssNet的方法用红色标注了出来。

  可见，NC-EssNet的精度高于所有基于位姿回归的方法。（AnchorNet需要额外在每个场景中训练）

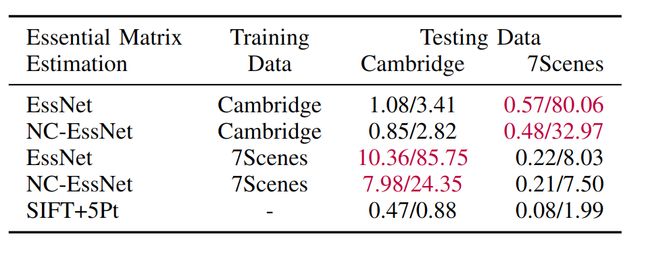
• RPR 的泛化性验证：

  在数据集１上训练，测试在数据集２上的精度：

  

  红色显示了泛化失败的例子。

  可能的原因：1.特征提取网络的泛化性不足。2.相对位姿回归层泛化性不足。3.两者都有

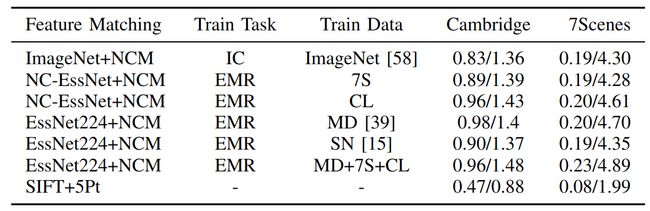
  首先验证特征提取网络。作者使用了C. Hybrid: Learnable Matching + 5-Point Solver中的模型，将可学习的提取和匹配网络换成不同数据集上训练得到的权重，考察其定位精度：

  

  IC表示图像分类任务，EMR表示本质矩阵回归任务。

  结果显示特征被如何训练得到的对定位精度的影响很小，因此得出结论：是回归层导致了泛化性的缺失。

  当从一对图像对中直接回归本质矩阵时，特征的匹配是在回归层中隐式的执行的。泛化性的缺失意味着回归网络不能正确地学习隐式匹配，虽然明确地学习匹配任务（混合模型）会导致更好的泛化性，但定位精度仍然不如SIFT+5pt准确。这种不准确性与CNN高层级特征图损失了定位精度有关，也就是说，来自后面各层的特征并未映射到原图的单个像素，而是映射到图像块。（这里考虑语义分割是如何解决定位精度的问题的）

  可以设计更好的网络结构来获得更好的局部特征：superpoint、D2-net

  另一种方法是训练网络检测异常值，然后作为匹配结果的后处理步骤。这种方法不利于定位网络向端到端的发展。

结论

RPR精度不如基于3D结构的原因在于回归层的输入数据已经损失了定位精度。（skip layers?）

本文提出预测本质矩阵的定位方法，避开了场景变化时要调整的超参数，轻量且泛化性强，不需要训练，不需要3D model。