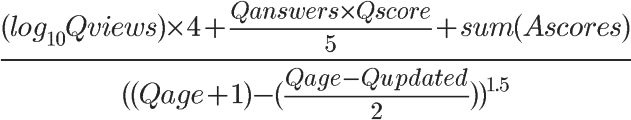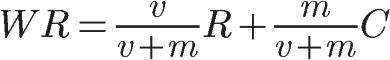Reddit评论排名算法
跳表(skiplist)学习笔记
这段时间公司做了个项目,在项目里面用到了redis,爱学习的我又一次翻出了redis的源代码,从头开始看了起来(没看完,哈哈~~),在这一次阅读中把redis的五大数据结构的代码给看了一遍,对于我这么一个菜鸟来说收获颇多,比如他的hash,list结构都没有使用我们平常使用的双向链表,而是使用一种非常节省内存的方式来实现了链表(zipmap和ziplist),还有zset就使用了跳表,其实levelDB也有使用跳表。
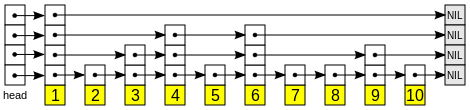
Skip List是在有序List(链表)数据结构的基础上的扩展,解决了有序链表结构查找特定值困难的问题,使用Skip List,可以使得在一个有序链表里查找特定值的时间复杂度为O(logn),他是一种可以代替平衡树的数据结构。Skip lists应用概率保证平衡,平衡树采用严格的旋转(比如平衡二叉树有左旋右旋)来保证平衡,因此Skip list比较容易实现,而且相比平衡树有着较高的运行效率。 其实现原理是链表中每一个元素都有N层(N为随机数,并且1<=N
[c]
#include
#include
#include
typedef int key_t;
typedef int value_t;
typedef struct node_t
{
key_t key;
value_t value;
struct node_t *forward[];
} node_t;
typedef struct skiplist
{
int level;
int length;
node_t *header;
} list_t;
#define MAX_LEVEL 16
#define SKIPLIST_P 0.25
node_t* slCreateNode(int level, key_t key, value_t value)
{
node_t *n = (node_t *)malloc(sizeof(node_t) + level * sizeof(node_t*));
if(n == NULL) return NULL;
n->key = key;
n->value = value;
return n;
}
list_t* slCreate(void)
{
list_t *l = (list_t *)malloc(sizeof(list_t));
int i = 0;
if(l == NULL) return NULL;
l->length = 0;
l->level = 0;
l->header = slCreateNode(MAX_LEVEL - 1, 0, 0);
for(i = 0; i < MAX_LEVEL; i++)
{
l->header->forward[i] = NULL;
}
return l;
}
int randomLevel(void)
{
int level = 1;
while ((rand()&0xFFFF) < (SKIPLIST_P * 0xFFFF))
level += 1;
return (levelheader;
int i;
for(i = list->level - 1; i >= 0; i-)
{
while(p->forward[i] && (p->forward[i]->key forward[i]->key == key){
return &p->forward[i]->value;
}
p = p->forward[i];
}
}
return NULL;
}
int slDelete(list_t *list, key_t key)
{
node_t *update[MAX_LEVEL];
node_t *p = list->header;
node_t *last = NULL;
int i = 0;
for(i = list->level - 1; i >= 0; i-){
while((last = p->forward[i]) && (last->key < key)){
p = last;
}
update[i] = p;
}
if(last && last->key == key){
for(i = 0; i < list->level; i++){
if(update[i]->forward[i] == last){
update[i]->forward[i] = last->forward[i];
}
}
free(last);
for(i = list->level - 1; i >= 0; i-){
if(list->header->forward[i] == NULL){
list->level-;
}
}
list->length-;
}else{
return -1;
}
return 0;
}
int slInsert(list_t *list, key_t key, value_t value)
{
node_t *update[MAX_LEVEL];
node_t *p, *node = NULL;
int level, i;
p = list->header;
for(i = list->level - 1; i >= 0; i-){
while((node = p->forward[i]) && (node->key < key)){
p = node;
}
update[i] = p;
}
if(node && node->key == key){
node->value = value;
return 0;
}
level = randomLevel();
if (level > list->level)
{
for(i = list->level; i < level; i++){
update[i] = list->header;
}
list->level = level;
}
node = slCreateNode(level, key, value);
for(i = 0; i < level; i++){
node->forward[i] = update[i]->forward[i];
update[i]->forward[i] = node;
}
list->length++;
return 0;
}
int main(int argc, char **argv)
{
list_t *list = slCreate();
node_t *p = NULL;
value_t *val = NULL;
//插入
for(int i = 1; i header->forward[0];
for(int i = 0; i < list->length; i++){
printf(“%d,%d\\n”, p->key, p->value);
p = p->forward[0];
}
getchar();
return 0;
}
用skip list实现实时排名?
问题是,怎么实现实时排名呢,对于有超过一亿用户,每天登录也有好几百万的博客来说,这不是个容易的问题。以前在博客魅力秀里,人数才不过几十万,都很困难。通过数据库基本没希望,你总不能每次要显示排名的时间,都执行下
SELECT COUNT(*) FROM Users WHERE 积分 < 我的积分;
吧,这种方法一般只有在用户不过万的时间才具有可行性。
以前也用过这样的方法。使用一个表记录积分和排名,初始的排名是脱机计算的,上线后,每当一个用户的积分发生变化,就统计一下新老积分之间的用户数,然后将自己的排名上升这么多位,把被我赶超的用户的排名都下降一位,用SQL语句示意就是这样
cnt = SELECT COUNT(*) FROM Users WHERE 积分 > 我的老积分 AND 积分 < 我的新积分;
UPDATE Users SET 排名 = 排名 - cnt WHERE UserID = 我的ID;
UPDATE Users SET 排名 = 排名 + 1 WHERE 积分 > 我的老积分 AND 积分 < 我的新积分;
使用这种方法,显示排名时是很快,因为排名已经计算好存在在数据库里了。但还是不行,只要人数过十万,积分更新比较频繁(如超过1秒10次),更新时的性能就不行了,并发冲突和死锁问题会非常严重。
可能要做实行排名,比较好的是用skip list,skip list是一个多级索引,如下图所示。由于高级的索引可以跳过大段大段的区间,使用skip list统计比指定的数值小的项的个数的时间复杂度是log(n)级的,节点中的数值发生变化时,更新的代价也是log(n)级。这样,使用skip list作为基本的数据结构实现实时排名是可行的。
skip list适合在内存中实现,一般来说内存的大小不是问题,即使对于博客这样有一亿用户的系统,就算每个用户占用100个字节(良好的实现应该可以做到50个字节左右),总共也不过10G内存,单机就可放得下。不过以下两个问题是需要处理的。
一是单机的处理能力可能跟不上,虽然skip list为纯内存数据结构,但如果一秒有上千次显示排名请求,系统就很可能撑不住。解决这一问题有两个方法,用多个skip list备份,或者按积分区间对skip list进行划分。第二个问题是skip list与数据库的同步。原始的积分信息当然是存储在数据库里的,skip list只不过是一种索引机制。两者同步可以由应用负责,即应用更新积分时同时更新数据库和skip list,也可以通过回放数据库更新日志(如MySQL的binlog或使用触发器来记录日志)来更新skip list。考虑到skip list程序可能崩溃,不能假设skip list中的积分与数据库中的积分总是一致的,这样更新skip list时,需要指定要更新的用户ID而不是用户的新老积分,这样,就需要在skip list的基础上增加一个哈希表,记录用户ID到skip list节点的映射关系。
一个好消息是这样的数据结构我们去年已经做了,当时的skip list是准备用在论坛里用于实现快速跳页的(因为skip list也可以高效定位第n个节点),但后来没用上。相信经过小规模的改造,可能就能用来实现实时排名。
初步的实现呢,只需要用以下的一张数据库表可能就行了。
CREATE TABLE BlogScoreSummary (
Score INT, -- 分值
Count INT, -- 积分为这一分值的人数
IDX BSS_SCORE_COUNT(Score, Count)
);
这样,计算排名时只需要用以下查询
SELECT SUM(Count) FROM BlogScoreSummary WHERE Score > ?;
这一查询会用索引,并且由于排名高的人被浏览的次数多,这个查询每次需要遍历求和的项平均就不大(查询中指定的参数越小,查询每次需要遍历求和的项就越多),因此很可能用数据库就可以搞定了。如果一台数据库不行,可以用复制搞个几十台嘛,反正这个表也很小。
更新的时候也很简单,只要把原积分对应的人数--,新积分对应的人数++就行了。
嗯哼,这么好的方法,竟然是巴望暴富的男人想出来的。
Reddit排名算法工作原理
这是一篇继《Hacker News 排名算法工作原理》之后的又一篇关于排名算法的文章。这次我将跟大家探讨一下Reddit的文章排名算法和评论排名算法的工作原理。Reddit使用的算法也是很简单,容易理解和实现。这篇文章里我将会对其进行深入分析。
首先我们关注的是文章排名算法。第二部分将重点介绍评论排名算法,Reddit的评论排名跟文章排名使用的不是同一种算法(这点跟Hacker News不一样),Reddit的评论排名算法非常有趣,它是由xkcd的作者Randall Munroe发明的。
深入研究文章排名算法代码
Reddit的源代码是开源的,你可以下载它的任意代码。它是用Python写成的,代码放在这里。里面的排名算法部分是用Pyrex实现的,这是一种开发Python的C语言扩展的编程语言。这里用Pyrex主要是出于速度的考虑。我用纯Python重写了他们的Pyrex实现,这样更容易阅读。
Reddit缺省的排名是’热门‘排名,实现代码如下:
#Rewritten code from /r2/r2/lib/db/_sorts.pyx
from datetime import datetime, timedelta
from math import log
epoch = datetime(1970, 1, 1)
def epoch_seconds(date):
"""Returns the number of seconds from the epoch to date."""
td = date - epoch
return td.days * 86400 + td.seconds + (float(td.microseconds) / 1000000)
def score(ups, downs):
return ups - downs
def hot(ups, downs, date):
"""The hot formula. Should match the equivalent function in postgres."""
s = score(ups, downs)
order = log(max(abs(s), 1), 10)
sign = 1 if s > 0 else -1 if s < 0 else 0
seconds = epoch_seconds(date) - 1134028003
return round(order + sign * seconds / 45000, 7)
这个“热门“排名算法用数学公式表达是下面这个样子(我从SEOmoz找到了它,但我怀疑他们未必是原作者):
文章提交时间对排名的影响
文章提交时间对排名的影响可以总结为以下几点:
-
提交时间对排名影响巨大,越新的文章排名会越高
-
文章排名得分不会随时间的流逝而降低,但新文章会比老文章获得更高的分。这跟Hacker News的排名算法有很大区别,它的得分会随时间流逝而降低。
下面是一个图片,表现的是具有相同支持和反对的票数,但时间不同的文章的排名得分情况:
对数加强
Reddit在‘热门’排名中使用了对数函数来强化前几票的份量。基本是这个原理:
-
前10个赞成票的份量和后面100个的份量,以及再后面1000票的份量是相同的,以此类推
下面是效果图:
如果不使用对数加强,则分数会是这样:
反对票对排名的影响
Reddit是少数几个能投反对票的网站之一。就像你从代码里看到的,一篇文章的的’得分‘定义如下:
-
up_votes - down_votes
这就是说,我们可以把它表现为下图:
这种计算方式会对既有很的赞成票,又有很多反对票的文章(比如很有争议的文章)带来重大影响,它们可能会比那些只有很少赞成票的文章获得更低的分数。这也就说明了为什么小猫小狗之类的帖子(以及其它无争议的文章)会获得如此高的评分。

对Reddit文章排名算法的总结
-
提交时间是一项非常重要的指标,新文章比老文章得分更高
-
头10个赞成票的份量和后100个的份量相同。获得10个赞成票和获得50个赞成票的排名很接近
-
具有相近赞成票和反对票数的有争议文章会比只获得赞成票的排名低。
Reddit评论排名算法工作原理
xkcd网站的Randall Munroe是Reddit网站上的‘最佳文章’排名算法的发明者。他写了一篇很好的文章来解释它。
-
reddit’s new comment sorting system
你应该读一读这篇文章,它以很通俗的语言解释了这个算法。这篇的文章的重点是:
-
‘热门‘排名算法对评论进行排名不是很有效,它会显得对早期的评论过于偏爱。
-
在一个评论系统中,我们的目的是找出最佳评论,不论它是什么时间提交的。
-
1927年Edwin B. Wilson找到了一种很好的算法,被叫做”Wilson score interval”,它可以被用于“信任排序(the confidence sort)”
-
信任排序把文章的获得的票数当作全体读者的一个抽样统计——就像一次民意测验。
-
《How Not To Sort By Average Rating》这篇文章对这种信任评级算法做了详细的解释,绝对值得一读!
深入分析评论排序代码
Reddit里的信任排序算法是在_sorts.pyx这个文件里实现的,我用纯Python重写了它们的Pyrex实现(同时去掉了其中的缓存优化代码):
#Rewritten code from /r2/r2/lib/db/_sorts.pyx from math import sqrt def _confidence(ups, downs): n = ups + downs if n == 0: return 0 z = 1.0 #1.0 = 85%, 1.6 = 95% phat = float(ups) / n return sqrt(phat+z*z/(2*n)-z*((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n) def confidence(ups, downs): if ups + downs == 0: return 0 else: return _confidence(ups, downs)信任排序使用Wilson score interval算法,它的数学表达式是这样的:
在上面的公式中,各个参数的定义如下:
-
p是支持票的百分比
-
n总票数
-
zα/2是正态分布(1-α/2)分位数
我们对上面的介绍做一些总结:
-
信任排序是把票数看作一次全体读者的抽样调查
-
信任排序会给一条评论一个临时评级,认为它有85%的可信度
-
票数越多,可信度越高
-
Wilson’s interval算法能很好的处理票数很少和低端概率情况
Randall在他的文章里对信任排序的工作原理给了一个很好的例子:
如果一条评论只有一个赞成票和0个反对票,它有100%的支持率,但因为投票数太少,系统将会把它放在排名底部。但如果它有10个赞成票,而其只有1个反对票,那系统将会把它放到比具有40个赞成票和20个反对票的评论更高的排名上——可以推断出,当这个评论获得40个赞成票时,它极有可能获得的反对票会少于20。这种算法最好的部分是,如果推断错了,那它会很快的获得更多的数据来证明,因为它已经被排到了顶部。
发表时间对排名的影响:没有!
信任排序一个优点是评论发表时间是不产生影响作用的(这跟‘热门排序’和Hacker News的排名算法是不一样的)。评论是通过信任评级,通过数据取样计算,一条评论获得的票数越多,它能获得的评级越接近他的真实的得分。
图表视图
让我们把信任排序做成图表,看一看它是如何影响评论排序的。我们使用Randall的例子:
可以看到,信任排序并不在意一条评论获得了多少票数,它关注的是它的支持率和数据采样规模!
排序之外的应用
正像Evan Miller所说的,Wilson’s score interval算法可以在非排名应用里使用,他列举了3个例子:
-
检查垃圾信息:看过这条信息的人中有多大比例认为它是垃圾信息?
-
制作“最优”排名:看过这条信息的人中有多大比例认为它是“最好的….”?
-
制作“邮件转发”排名:看过条信息这的人中有多大比例点击了‘Email’按钮?
使用这个算法你只需要两个数据:
-
取样总数
-
支持数
这个算法是如此有效,但很奇怪很多的网站如今仍然是最原始的评级方法,这包括著名的亚马逊,它仍然使用“得分 = 支持票 / 总票数”。
结论
我希望这篇文章对你们有些用处,如有任何疑问,请在评论里写出。
祝编程快乐

:)
Reddit排名算法工作原理
这是一篇继《Hacker News 排名算法工作原理》之后的又一篇关于排名算法的文章。这次我将跟大家探讨一下Reddit的文章排名算法和评论排名算法的工作原理。Reddit使用的算法也是很简单,容易理解和实现。这篇文章里我将会对其进行深入分析。
首先我们关注的是文章排名算法。第二部分将重点介绍评论排名算法,Reddit的评论排名跟文章排名使用的不是同一种算法(这点跟Hacker News不一样),Reddit的评论排名算法非常有趣,它是由xkcd的作者Randall Munroe发明的。
深入研究文章排名算法代码
Reddit的源代码是开源的,你可以下载它的任意代码。它是用Python写成的,代码放在这里。里面的排名算法部分是用Pyrex实现的,这是一种开发Python的C语言扩展的编程语言。这里用Pyrex主要是出于速度的考虑。我用纯Python重写了他们的Pyrex实现,这样更容易阅读。
Reddit缺省的排名是’热门‘排名,实现代码如下:
#Rewritten code from /r2/r2/lib/db/_sorts.pyx
from datetime import datetime, timedelta
from math import log
epoch = datetime(1970, 1, 1)
def epoch_seconds(date):
"""Returns the number of seconds from the epoch to date."""
td = date - epoch
return td.days * 86400 + td.seconds + (float(td.microseconds) / 1000000)
def score(ups, downs):
return ups - downs
def hot(ups, downs, date):
"""The hot formula. Should match the equivalent function in postgres."""
s = score(ups, downs)
order = log(max(abs(s), 1), 10)
sign = 1 if s > 0 else -1 if s < 0 else 0
seconds = epoch_seconds(date) - 1134028003
return round(order + sign * seconds / 45000, 7)
这个“热门“排名算法用数学公式表达是下面这个样子(我从SEOmoz找到了它,但我怀疑他们未必是原作者):
文章提交时间对排名的影响
文章提交时间对排名的影响可以总结为以下几点:
-
提交时间对排名影响巨大,越新的文章排名会越高
-
文章排名得分不会随时间的流逝而降低,但新文章会比老文章获得更高的分。这跟Hacker News的排名算法有很大区别,它的得分会随时间流逝而降低。
下面是一个图片,表现的是具有相同支持和反对的票数,但时间不同的文章的排名得分情况:
对数加强
Reddit在‘热门’排名中使用了对数函数来强化前几票的份量。基本是这个原理:
-
前10个赞成票的份量和后面100个的份量,以及再后面1000票的份量是相同的,以此类推
下面是效果图:
如果不使用对数加强,则分数会是这样:
反对票对排名的影响
Reddit是少数几个能投反对票的网站之一。就像你从代码里看到的,一篇文章的的’得分‘定义如下:
-
up_votes - down_votes
这就是说,我们可以把它表现为下图:
这种计算方式会对既有很的赞成票,又有很多反对票的文章(比如很有争议的文章)带来重大影响,它们可能会比那些只有很少赞成票的文章获得更低的分数。这也就说明了为什么小猫小狗之类的帖子(以及其它无争议的文章)会获得如此高的评分。

对Reddit文章排名算法的总结
-
提交时间是一项非常重要的指标,新文章比老文章得分更高
-
头10个赞成票的份量和后100个的份量相同。获得10个赞成票和获得50个赞成票的排名很接近
-
具有相近赞成票和反对票数的有争议文章会比只获得赞成票的排名低。
Reddit评论排名算法工作原理
xkcd网站的Randall Munroe是Reddit网站上的‘最佳文章’排名算法的发明者。他写了一篇很好的文章来解释它。
-
reddit’s new comment sorting system
你应该读一读这篇文章,它以很通俗的语言解释了这个算法。这篇的文章的重点是:
-
‘热门‘排名算法对评论进行排名不是很有效,它会显得对早期的评论过于偏爱。
-
在一个评论系统中,我们的目的是找出最佳评论,不论它是什么时间提交的。
-
1927年Edwin B. Wilson找到了一种很好的算法,被叫做”Wilson score interval”,它可以被用于“信任排序(the confidence sort)”
-
信任排序把文章的获得的票数当作全体读者的一个抽样统计——就像一次民意测验。
-
《How Not To Sort By Average Rating》这篇文章对这种信任评级算法做了详细的解释,绝对值得一读!
深入分析评论排序代码
Reddit里的信任排序算法是在_sorts.pyx这个文件里实现的,我用纯Python重写了它们的Pyrex实现(同时去掉了其中的缓存优化代码):
#Rewritten code from /r2/r2/lib/db/_sorts.pyx from math import sqrt def _confidence(ups, downs): n = ups + downs if n == 0: return 0 z = 1.0 #1.0 = 85%, 1.6 = 95% phat = float(ups) / n return sqrt(phat+z*z/(2*n)-z*((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n) def confidence(ups, downs): if ups + downs == 0: return 0 else: return _confidence(ups, downs)信任排序使用Wilson score interval算法,它的数学表达式是这样的:
在上面的公式中,各个参数的定义如下:
-
p是支持票的百分比
-
n总票数
-
zα/2是正态分布(1-α/2)分位数
我们对上面的介绍做一些总结:
-
信任排序是把票数看作一次全体读者的抽样调查
-
信任排序会给一条评论一个临时评级,认为它有85%的可信度
-
票数越多,可信度越高
-
Wilson’s interval算法能很好的处理票数很少和低端概率情况
Randall在他的文章里对信任排序的工作原理给了一个很好的例子:
如果一条评论只有一个赞成票和0个反对票,它有100%的支持率,但因为投票数太少,系统将会把它放在排名底部。但如果它有10个赞成票,而其只有1个反对票,那系统将会把它放到比具有40个赞成票和20个反对票的评论更高的排名上——可以推断出,当这个评论获得40个赞成票时,它极有可能获得的反对票会少于20。这种算法最好的部分是,如果推断错了,那它会很快的获得更多的数据来证明,因为它已经被排到了顶部。
发表时间对排名的影响:没有!
信任排序一个优点是评论发表时间是不产生影响作用的(这跟‘热门排序’和Hacker News的排名算法是不一样的)。评论是通过信任评级,通过数据取样计算,一条评论获得的票数越多,它能获得的评级越接近他的真实的得分。
图表视图
让我们把信任排序做成图表,看一看它是如何影响评论排序的。我们使用Randall的例子:
可以看到,信任排序并不在意一条评论获得了多少票数,它关注的是它的支持率和数据采样规模!
排序之外的应用
正像Evan Miller所说的,Wilson’s score interval算法可以在非排名应用里使用,他列举了3个例子:
-
检查垃圾信息:看过这条信息的人中有多大比例认为它是垃圾信息?
-
制作“最优”排名:看过这条信息的人中有多大比例认为它是“最好的….”?
-
制作“邮件转发”排名:看过条信息这的人中有多大比例点击了‘Email’按钮?
使用这个算法你只需要两个数据:
-
取样总数
-
支持数
这个算法是如此有效,但很奇怪很多的网站如今仍然是最原始的评级方法,这包括著名的亚马逊,它仍然使用“得分 = 支持票 / 总票数”。
结论
我希望这篇文章对你们有些用处,如有任何疑问,请在评论里写出。
祝编程快乐

:)
Hacker News 排名算法工作原理
这篇文章我要向大家介绍Hacker News网站的文章排名算法工作原理,以及如何在自己的应用里使用这种算法。这个算法非常的简单,但却在突出热门文章和遴选新文章上表现的异常优秀。
深入 news.arc 程序代码
Hacker News是用Arc语言开发的,这是一种Lisp方言,由Y Combinator投资公司创始人Paul Graham创造。Hacker News的开源的,你可以在arclanguage.org找到它的源代码。深入发掘 news.arc 程序,你会找到这段排名算法代码,就是下面这段:
; Votes divided by the age in hours to the gravityth power.
; Would be interesting to scale gravity in a slider.
(= gravity* 1.8 timebase* 120 front-threshold* 1
nourl-factor* .4 lightweight-factor* .3 )
(def frontpage-rank (s (o scorefn realscore) (o gravity gravity*))
(* (/ (let base (- (scorefn s) 1)
(if (> base 0) (expt base .8) base))
(expt (/ (+ (item-age s) timebase*) 60) gravity))
(if (no (in s!type 'story 'poll)) 1
(blank s!url) nourl-factor*
(lightweight s) (min lightweight-factor*
(contro-factor s))
(contro-factor s))))
本质上,这段 Hacker News采用的排名算法的工作原理看起来大概是这个样子:
Score = (P-1) / (T+2)^G 其中, P = 文章获得的票数( -1 是去掉文章提交人的票) T = 从文章提交至今的时间(小时) G = 比重,news.arc里缺省值是1.8
正如你看到的,这个算法很容易实现。在下面的内容里,我们将会看到这个算法是如何工作的。
比重(G)和时间(T)对排名的影响
比重和时间在文章的排名得分上有重大的影响。正常情况下如下面所述:
-
当T增加时文章得分会下降,这就是说越老的文章分数会越底。
-
当比重加大时,老的文章的得分会减的更快
为了能视觉呈现这个算法,我们可以把它绘制到Wolfram Alpha。
得分随着时间是如何变化的
你可以看到,随着时间的流逝,得分骤然下降,例如,24小时前的文章的分数变的非常低——不管它获得了如何多的票数。
Plot语句:
plot( (30 - 1) / (t + 2)^1.8, (60 - 1) / (t + 2)^1.8, (200 - 1) / (t + 2)^1.8 ) where t=0..24比重参数是如何影响排名的
图中你可以看到,比重越大,得分下降的越快。
Plot语句:
plot( (p - 1) / (t + 2)^1.8, (p - 1) / (t + 2)^0.5, (p - 1) / (t + 2)^2.0 ) where t=0..24, p=10Python语言实现
之前已经说了,这个评分算法很容易实现:
def calculate_score(votes, item_hour_age, gravity=1.8): return (votes - 1) / pow((item_hour_age+2), gravity)关键是要理解算法中的各个因素对评分的影响,这样你可以在你的应用中进行定制。我希望这篇文章已经向你说明了这些

祝编程快乐!
编辑:
Paul Graham 分享了修正后的HN 排名算法:
(= gravity* 1.8 timebase* 120 front-threshold* 1 nourl-factor* .4 lightweight-factor* .17 gag-factor* .1) (def frontpage-rank (s (o scorefn realscore) (o gravity gravity*)) (* (/ (let base (- (scorefn s) 1) (if (> base 0) (expt base .8) base)) (expt (/ (+ (item-age s) timebase*) 60) gravity)) (if (no (in s!type 'story 'poll)) .8 (blank s!url) nourl-factor* (mem 'bury s!keys) .001 (* (contro-factor s) (if (mem 'gag s!keys) gag-factor* (lightweight s) lightweight-factor* 1))))):)
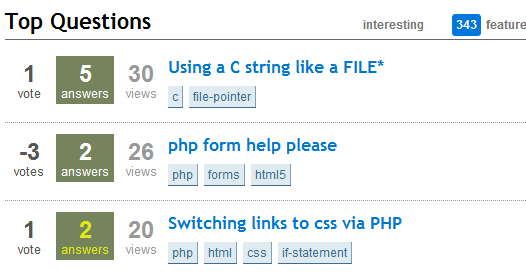
数学之美:StackOverflow问答排名算法
先前的文章介绍了StackOverflow的系统架构,这次继续排序话题,学习的是StackOverFlow的排序算法。
StackOverflow的排序共分为两类,1个是问题排序,1个是答案排序。这里主要介绍的是关于热门问题的排序。
在分析问题前可以先考虑下,如果是你来做这个排名算法需要考虑哪些因素?
1、问题的投票人数,StackOverflow允许用户投反对票,所以这里可以使用绝对投票数,即正面票-负面票数量。绝对数越高问题越热门。
2、问题浏览量,或是有效浏览量,有效浏览量可以建立一个停留时间的阀值去衡量。浏览的越多则越热门。
3、问题的答案数,理论上说答案越多则问题的越热门,但这也并不绝对,有些好的问答可能只有一个好的答案。
4、问题答案的认可数,即是否存在一个被大量认可的答案。这里存在两种情况,被提问者认可或被其他访问者投票。多少的投票量可以认为是问题答案被认可也是需要考虑的问题。
5、问题的提问时间和问题的最后答复时间,问题的受欢迎程度应该是随时间变长而变得不热门。
5、提问者的声望和回答问题的声望,声望越高的问题肯定质量越到,越值得去推荐。
在08年8月23日的时候,StackOverflow的创始人 Jeff Atwood曾经公布了一个热门问题的排名算法(链接):具体为
此算法目前是否还继续使用或者是否改变不得而知。下面我们详细介绍下问题排名中涉及到的变量。将其转化成Python代码为:
import time, math
def hot (Qviews, Qanswers, Qscore, Ascore, date_ask, date_active):
Qage = round((time.time() - date_ask) / 3600)
Qupdated = round((time.time() - date_active) / 3600)
return (math.log10(Qviews) * 4 + Qanswers * Qscore / 5 + Ascore )/(pow((Qage + 1) - (Qage - Qupdated) / 2,1.5))
1、Qviews(问题的浏览次数)
- log(Qviews)*4
某个问题的浏览次数越多,就代表越受关注,得分也就越高。这里使用了以 10为底的对数,用意是当访问量越来越大,它对得分的影响将不断变小。
2、Qscore(问题得分)和 Qanswers(回答的数量)
-(Qanswers * Qscore)/5
Qscore(问题得分)= 赞成票-反对票。如果某个问题越受到好评,排名自然应该越靠前。Qanswers 表示回答的数量,代表有多少人参与这个问题。这个值越大,得分将成倍放大。这里需要注意的是,如果无人回答,Qanswers 就等于0,这时 Qscore 再高也没用,意味着再好的问题,也必须有人回答,否则进不了热点问题排行榜。
3、Ascores(回答得分)
-sum(Ascores)
一般来说,”回答”比”问题”更有意义。这一项的得分越高,就代表回答的质量越高。但是简单加总的设计还不够全面。这里有两个问题。首先,一个正确的回答胜过一百个无用的回答,但是,简单加总会导致,1个得分为 100 的回答与 100 个得分为 1 的回答,总得分相同。其次,由于得分会出现负值,因此那些特别差的回答,会拉低正确回答的得分。
4、Qage(距离问题发表的时间)和 Qupdated(距离最后一个回答的时间)
-((Qage+1) - ((Qage - Qupdated)/2)) ^ 1.5
Qage 和 Qupdated 的单位都是小时。如果一个问题的存在时间越久,或者距离上一次回答的时间越久,Qage 和 Qupdated 的值就相应增大。也就是说,随着时间流逝,这两个值都会越变越大,导致分母增大,因此总得分会越来越小。
总结:Stack Overflow 热点问题的排名,与参与度(Qviews 和 Qanswers)和质量(Qscore 和 Ascores)成正比,与时间(Qage 和 Qupdated)成反比。
关于上述的答案是否合理的,是否可以再改良,答案是肯定的,如果是你你会怎样去推荐热门问答呢?
参考地址:http://meta.stackoverflow.com/questions/11602/what-formula-should-be-used-to-determine-hot-questions
数学之美:Reddit评论排名算法
上一篇文章介绍了Reddit的排名算法,今天继续上一篇文章,需要学习的是reddit的评论排名算法。与文章新闻类排名不同的事,评论类的算法可能发表时间没有什么关系。
目前很多网站采用的评论排名主要有两种,即绝对好评数(好评减去差评)和好评率(好评/总评)。这两种评价方式 都存在很明显的缺陷,以下为事例:
A:好评550; 差评450B:好评60;差评40C:好评1;差评0D:好评9,差评1首先是A与B比较,A的绝对好评数是550-450=100,B的绝对好评数是60-40=20,从绝对好评数比较,A的排名应该在B的前面;A的好评率为550/(450+550)=55%,B的好评率为60/(40+60)=60%,从好评率来说B的排名要比A的排名好。
再来比较下C与D,从好评率出发,C的好评率为100%,而D的好评率为9/(1+9)=90%,单纯从数据上看D的排名要比C的排名落后。对于评论排名上述的方法是否是我们所需要的呢?这样的计算才能更好的体现评论价值?正确的排名算法应该是怎样的?
我们先做如下设定:
每个用户的投票都是独立事件。用户只有两个选择,要么投好评,要么投差评。如果投票总人数为n,其中好评为k,那么好评率p就等于k/n。如果你熟悉统计学,可能已经看出来了,p服从一种统计分布,叫做“两项分布”(binomial distribution)。
p越大,就代表这个项目的好评比例越高,越应该排在前面。但是,p的可信性,取决于有多少人投票,如果样本太小,p就不可信。由于p服从”两项分布”,因此我们可以计算出p的置信区间。所谓“置信区间”,就是说,以某个概率而言,p会落在的那个区间。比如,某个产品的好评率是 80%,但是这个值不一定可信。根据统计学,我们只能说,有 95% 的把握可以断定,好评率在 75% 到 85% 之间,即置信区间是[75%, 85%]。
通过上面的分析,我们就可以推断出,如果要给一个评论进行排名,就需要考虑一下内容:
计算每个评论的”好评率”计算每个”好评率”的置信区间(以 95% 的概率)。根据置信区间的下限值,进行排名。这个值越大,排名就越高。这样做的原理是,置信区间的宽窄与样本的数量有关。比如,A有 8 张赞成票,2张反对票;B有 80 张赞成票,20张反对票。这两个项目的赞成票比例都是 80%,但是B的置信区间(假定[75%, 85%])会比A(假定[70%, 90%])窄得多,因此B的置信区间的下限值(75%)会比A(70%)大,所以B应该排在A前面。
置信区间的实质,就是进行可信度的修正,弥补样本量过小的影响。如果样本多,就说明比较可信,不需要很大的修正,所以置信区间会比较窄,下限值会比较大;如果样本少,就说明不一定可信,必须进行较大的修正,所以置信区间会比较宽,下限值会比较小。
二项分布的置信区间有多种计算公式,最常见的是“正态区间”(Normal approximation interval),教科书里几乎都是这种方法。但是,它只适用于样本较多的情况(np > 5 且 n (1 − p) > 5),对于小样本,它的准确性很差。
1927年,美国数学家 Edwin Bidwell Wilson 提出了一个修正公式,被称为“威尔逊区间”,很好地解决了小样本的准确性问题。Reddit 目前使用的是评论算法就是基于威尔逊得分区间 (Wilson score interval)。具体代码片段可从开放的源代码中找到,将其转化成Python代码后:
from math import sqrt
def _confidence(ups, downs):
n = ups + downs
if n == 0:
return 0
z = 1.0 #1.0 = 85%, 1.6 = 95%
phat = float(ups) / n
return (phat+z*z/(2*n)-z*sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n)
def confidence(ups, downs):
if ups + downs == 0:
return 0
else:
return _confidence(ups, downs)
使用到的威尔逊得分区间具体公式如下:
其中
p 是好评率n 是总投票数Z (1-α/2) 表示对应某个置信水平的z统计量,这是一个常数,可以通过查表得到。一般情况下,在 95% 的置信水平下,z统计量的值为1.96。可以公式看到,当n的值足够大时,这个下限值会趋向。如果n非常小(投票人很少),这个下限值会大大小于
。实际上,起到了降低”好评率”的作用,使得该评论的得分变小、排名下降。
威尔逊得分区并不关心一个评论的投票数,而关心好评数和投票总数或采样大小的相对关系!
上图是根据威尔逊得分区计算出来的值:一个评论有1个好评,没有差评,它的支持率是100%,但是由于数据量过小,系统还是会把它放到底部。 但如果,它有10个好评,1个差评,系统可能会有足够的信息把他放到一个有着40个好评,20个差评的评论之前。因为我们基本确认当它有了40个好评的时候,它收到的差评会少于20个。最好的一点是,一旦这个算法出错了(算法有15%的失效概率),它会很快拿到更多的数据,因为它被排到了前面。
威尔逊得分区间不仅仅用于评论排名,它还试用于以下情景:
参考文章:
http://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval#Wilson_score_interval
http://blog.reddit.com/2009/10/reddits-new-comment-sorting-system.html
http://www.evanmiller.org/how-not-to-sort-by-average-rating.html
数学之美:Hacker News的热门排名算法
Hacker News 是一家关于计算机黑客和创业公司的社会化新闻网站,由 Paul Graham 的创业孵化器 Y Combinator 创建。与其它社会化新闻网站不同的是 Hacker News 没有踩或反对一条提交新闻的选项(不过评论还是可以被有足够 Karma 的用户投反对票,或是投支持票);只可以赞或是完全不投票。简而言之,Hacker News 允许提交任何可以被理解为“任何满足人们求知欲”的新闻。
每个新闻标题前面有一个向上的三角形,如果你觉得这个内容很好,就点击一下,投上一票。根据得票数,系统自动统计出热门文章排行榜。但是,并非得票最多的文章排在第一位,还要考虑时间因素,新文章应该比旧文章更容易得到好的排名。
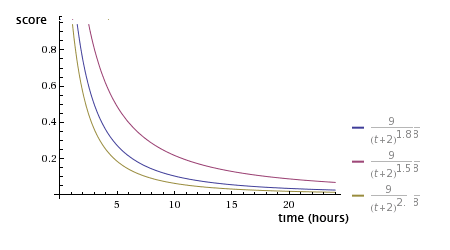
Hacker News 采用公式 (p - 1) / (t + 2)^1.5 做为排行依据(Hacker News使用Paul Graham开发的Arc语言编写,源码可以从arclanguage.org下载),其中P是投票数量,t是发表以来的时间,小时计。后来AMIX.DK 给出公式 Score = (P-1) / (T+2)^G 推广了上面的公式,Hacker News的公式变成了一个特例,其在G=1.5时的应用。历史上Hacker News有用G=1.8。
第一个因素是得票数P
在其他条件不变的情况下,得票越多,排名越高。从下图可以看到,有三个同时发表的帖子,得票分别为200票、60票和30票(减1后为199、59和29),分别以黄色、紫色和蓝色表示。在任一个时间点上,都是黄色曲线在最上方,蓝色曲线在最下方。
为什么是P-1?网络上的一种解释是,很多文章作者在提交的时候会给自己投上一票。其实更重要的原因是文章发布初期的投票数对排名影响非常的,仅仅是自己给自己投的一票,也占非常大的作用。
假设P不去减去1,那公式为: p / (t + 2)^1.5
如果一个作者发布完就给自己投票,那么文章的得分为1/(0+2)^1.5=0.3535 。假设另外一篇文章发布了8小时,那么需要多少的投票呢?x/(8+2)^1.5>0.3535 X>11.17~ 即一天前的帖子要有12票才能超过新提交的文章,这显然不合理。
这个具体减多少还要视网络环境而定,要是换在国内,估计P-100还不够。另外如果你不期望“高投票文章”与“低投票文章差距过大,可以在得票数上加一个小于1的指数,比如(P-1)^0.8。
第二个因素是距离发帖时间T
在其他条件不变的情况下,越是新发表的帖子,排名越高。或者说,一个帖子的排名,会随着时间不断下降。
从前一张图可以看到,经过24小时之后,所有帖子的得分基本上都小于1,这意味着它们都将跌到排行榜的末尾,保证了排名前列的都将是较新的内容。
如果,用户的第一个投票是在当前,1小时,2小时获得时,这个曲线的变化是什么呢?如下图,曲线斜率从大到小分别是当前、1小时、2小时。可以看到第一个投票的作用不断弱化,其权重不断降低。
第三个因素是重力因子G
它的数值大小决定了排名随时间下降的速度。从下图可以看到,三根曲线的其他参数都一样,G的值分别为1.5、1.8和2.0。G值越大,曲线越陡峭,排名下降得越快。
为什么G=1.5,首先,G是干嘛的。毫无疑问,G这个数字既非时间,也非评价,其实它的主要目的是控制更新频率。G的值越大,score的衰减速度越快,排行的更新越频繁。所以,确定G值需要观察系统内部投票数在时间上的分布,然后根据需要的更新频次确定G的合理取值。越火爆、用户互动越频繁的社区,为了保证排行的稳定性(不要频繁大量的刷新),G值趋向于比较低。这就是为什么Hacker News从一开始的1.8修改成1.5,过段时间可能就变成1.2了。
数学之美:IMDB.COM排名算法
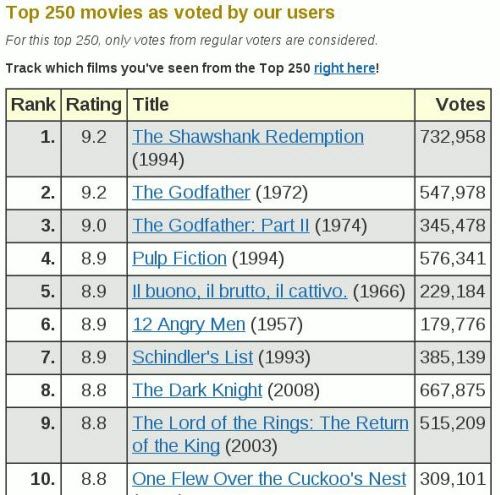
IMDB.COM是目前互联网上最为权威、系统、全面的电影资料网站,里面包括了几乎所有的电影,以及1982 年以后的电视剧集。 它所特有的电影评分系统深受影迷的欢迎,注册的用户可以给任何一部影片打分并加以评述,而网站又会根据影片所得平均分、选票的数目等计算得出影片的加权平均分并以此进行TOP250(最佳250部影片)和Bottom100(最差100部影片)的排行。
评选最佳250部电影时只考虑正式的投票者的投票结果。分值系统采用10分制,最低为awful(令人厌恶)的1分,最高为excellent(出类拔萃)的10分。值得注意的是,虽然很多影片在资料系统中得分很高,但由于未能达到TOP所要求的最低投票数而无法参加排行。
下面就一起来学习下IMDB所使用的排名算法。 imdb top 250用的是贝叶斯统计的算法得出的加权分(Weighted Rank-WR),公式如下:
- WR, 加权得分(weighted rating)。
- R,该电影的用户投票的平均得分(Rating)。
- v,该电影的投票人数(votes)。
- m,排名前 250 名的电影的最低投票数(现在为 3000)。
- C, 所有电影的平均得分(现在为6.9)。
仔细研究这个公式,你会发现,IMDB 为每部电影增加了 3000 张选票,并且这些选票的评分都为6.9。这样做的原因是,假设所有电影都至少有 3000 张选票,那么就都具备了进入前 250 名的评选条件;然后假设这 3000 张选票的评分是所有电影的平均得分(即假设这部电影具有平均水准);最后,用现有的观众投票进行修正,长期来看,v/(v+m)这部分的权重将越来越大,得分将慢慢接近真实情况。这样做拉近了不同电影之间投票人数的差异,使得投票人数较少的电影也有可能排名前列。
把这个公式写成更一般的形式:
- C,投票人数扩展的规模,是一个自行设定的常数,与整个网站的总体用户人数有关,可以等于每个项目的平均投票数。
- n,该项目的现有投票人数。
- x,该项目的每张选票的值。
- m,总体平均分,即整个网站所有选票的算术平均值。
这种算法被称为”贝叶斯平均”(Bayesian average)。因为某种程度上,它借鉴了”贝叶斯推断”(Bayesian inference)的思想:既然不知道投票结果,那就先估计一个值,然后不断用新的信息修正,使得它越来越接近正确的值。
在这个公式中,m(总体平均分)是”先验概率”,每一次新的投票都是一个调整因子,使总体平均分不断向该项目的真实投票结果靠近。投票人数越多,该项目的”贝叶斯平均”就越接近算术平均,对排名的影响就越小。因此,这种方法可以给一些投票人数较少的项目,以相对公平的排名。
“贝叶斯平均”也有缺点,主要问题是它假设用户的投票是正态分布。比如,电影A有 10 个观众评分,5个为五星,5个为一星;电影B也有 10 个观众评分,都给了三星。这两部电影的平均得分(无论是算术平均,还是贝叶斯平均)都是三星,但是电影A可能比电影B更值得看。
解决这个问题的思路是,假定每个用户的投票都是独立事件,每次投票只有n个选项可以选择,那么这就服从“多项分布”(Multinomial distribution),就可以结合贝叶斯定理,计算该分布的期望值。由于这涉及复杂的统计学知识,这里就不深入了,感兴趣的朋友可以继续阅读 William Morgan 的How to rank products based on user input。
另外对于无时间参与的评价系统,也可以参考威尔逊得分区,威尔逊得分分区的缺点在于排行榜前列总是那些票数最多的项目,新项目或者冷门的项目,很难有出头机会,排名可能会长期靠后。
参考地址:http://www.imdb.com/chart/top
IMDB评分排名算法
IMDB网站是目前互联网上最为权威、系统、全面的电影资料网站,里面包括了几乎所有的电影,以及1982 年以后的电视剧集。IMDB的资料中包括了影片的众多信息,演员,片长,内容介绍,分级 ,评论等,就个人买碟而言,很大程度上也是参考IMDB的得分。 它所特有的电影评分系统深受影迷的欢迎,注册的用户可以给任何一部影片打分并加以评述,而网站又会根据影片所得平均分、选票的数目等计算得出影片的加权平均分并以此进行TOP250(最佳250部影片)和Bottom100(最差100部影片)的排行。由于影片资料的更新和所得评分的不断变化,TOP250和Bottom100必定是份动态的名单,但大部分出色(或者说是受大众欢迎的)影片的位置会相对不变,于是这份TOP榜单也就有了窥视大众电影口味的意义。评选最佳250部电影时只考虑正式的投票者的投票结果。分值系统采用10分制,最低为awful(令人厌恶)的1分,最高为excellent(出类拔萃)的10分。值得注意的是,虽然很多影片在资料系统中得分很高,但由于未能达到TOP所要求的最低1250张的投票数而无法参加排行。因此,很多曲高和寡(至少在美国)的优秀影片未能列入其中。尽管如此,这份名单对选看影片仍具有重要的参考价值。
根据IMDB网站上公布的TOP250评分标准:
imdb top 250用的是贝叶斯统计的算法得出的加权分(Weighted Rank-WR),公式如下:
weighted rank (WR) = (v ÷ (v+m)) × R + (m ÷ (v+m)) × C
其中:
R = average for the movie (mean) = (Rating) (是用普通的方法计算出的平均分)
v = number of votes for the movie = (votes) (投票人数,需要注意的是,只有经常投票者才会被计算在内,这个下面详细解释)
m = minimum votes required to be listed in the top 250 (currently 1250) (进入imdb top 250需要的最小票数,只有三两个人投票的电影就算得满分也没用的)
C = the mean vote across the whole report (currently 6.9) (目前所有电影的平均得分)
IMDB上的评分完全来自于网民的评价,凭的是参与评价的网民的自身喜好,参与评分的网民越多,IMDB的评分越有可靠性。
这个估算比目前豆瓣所采用的简单平均分方法要科学的多,因为它既考虑了电影的受众人数,也考虑了优劣。比如一部电影只有10个人看过,这10个人都给它打10分,而另一部电影有10000人看过,平均分是9分,大家觉得哪个好?我想大部分人会相信是后者。所以这就是贝叶斯算法的依据。
看到这个公式,我们就能明白为什么IMDB的排名最有权威性,虽然它是一个以英美观众为主的网站,但依然受到全世界影迷的推崇,这和它以科学为主导的客观公正性是分不开的。别的各种所谓排行榜都可以伪造,可以花钱买,或者是一种商业游戏,但是IMDB不是,所以这就是它的价值。