通俗易懂地讲解《并查集》
本文著作权为本人所有,转载请注明出处。
正文:
谈到并查集,我只想感叹一句:
“你只看见我渺小的身躯,却没有看到我心中的那片森林。”
这,就是并查集思想最精妙之处.
理解下面三句话,并查集就学会了:
-
“并”的意思是把两个处在同一个连通分量的结点给并到一起.
-
“查”的意思是查找一个结点的根节点.
-
“并”的时候需要用到“查”
步骤:
1.查(“查”的意思是查找一个结点的根节点.)
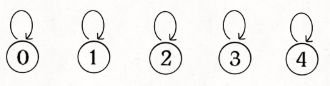
初始化一个 p a r e n t parent parent数组,里面存放每个节点的的父节点( p a r e n t [ i ] = i parent[i] = i parent[i]=i 的父节点).为什么要这个数组呢?
p a r e n t parent parent 数组可以表示一颗树!
其目的是为了查根节点,根据这个数组,我们不就可以“顺藤摸瓜”,找到每个节点的根节点了吗?
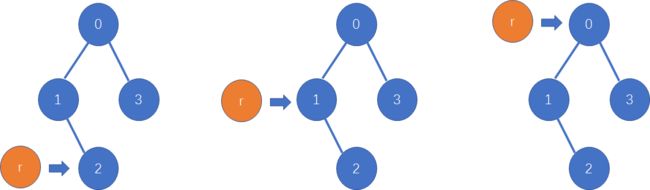
假如你在一个大家族里,大家族中的每个人都知道自己的父亲是谁,当有一天,你问你爸爸我的祖先是谁呀?你爸爸就会先问你爷爷,你爷爷就问你太爷爷,最后就能追溯到祖先 r o o t root root.
简单吧,这就实现了并查集中“查”的功能.
代码实现:
# 查根
def find(x, parent):
r = x # 假设根就是当前的结点
while r != parent[r]: # 如果假设不成立(r不是根节点),就继续循环
r = parent[r] # 假设根节点是当前节点的父节点,即往树的上面走一层
return r # 循环结束了,根也就找到了
为啥这句代码不成立的时候,就找到了根节点呢?
r != parent[r]
因为我们在初始化的时候,每个节点的根节点初始化为它自己,即我爸爸是我自己,这就是根节点和其他节点的不同之处!!!当 r == parent[r] 的时候,不就说明r是根节点了吗.
# parent 数组的初始化
parent = defaultdict(int)
for i in range(len(M)):
parent[i] = i # i的爸爸是他自己
2.并(“并”的意思是把两个处在同一个连通分量的结点给并到一起.)
并就更简单了。
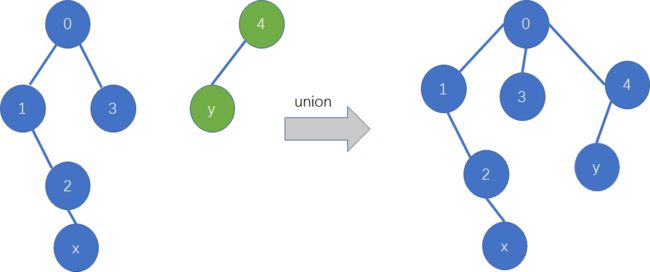
比如有两个节点 x和y, 我们就查一下x的根节点和y的根节点(并的时候用到了查)是不是同一个节点(咱们的祖先是不是同一个人),如果是,那么x和y本来就是一家人,不用做任何操作。
如果发现x和y的祖先不同,必须有一个人要迁移户口,例如就让y的祖先做x祖先的儿子,这样x 和 y还是成为一家人了(实现了并操纵)。
代码:
def union(x, y, parent):
x_root = find(x, parent)
y_root = find(y, parent)
# 将x作为根节点
if x_root != y_root:
parent[y_root] = x_root
应用到实际问题中?
这里推荐leetcode上的一道题—《朋友圈》,供大家练习,将上面学到的知识加以运用。
链接:
https://leetcode-cn.com/problems/friend-circles/solution/union-find-suan-fa-xiang-jie-by-labuladong/
题目:
班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。
给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。如果M[i][j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
示例 1:
输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出: 2
说明:已知学生0和学生1互为朋友,他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。
示例 2:输入:
[[1,1,0],
[1,1,1],
[0,1,1]]
输出: 1
说明:已知学生0和学生1互为朋友,学生1和学生2互为朋友,所以学生0和学生2也是朋友,所以他们三个在一个朋友圈,返回1。
解题思路用一句话概括就是:
把有朋友关系的人用union()函数合并到一起,看看合并以后还有几个根节点,一个根节点代表一个朋友圈。
附上解答代码:
from collections import defaultdict
# 查根
def find(x, parent):
r = x
while r != parent[r]:
r = parent[r]
return r
def union(x, y, parent):
x_root = find(x, parent)
y_root = find(y, parent)
# 将x作为根节点
if x_root != y_root:
parent[y_root] = x_root
class Solution(object):
def findCircleNum(self, M):
"""
:type M: List[List[int]]
:rtype: int
"""
parent = defaultdict(int)
ans = set()
if not M:
return 0
for i in range(len(M)):
parent[i] = i
for i in range(len(M)):
for j in range(i, len(M[0])):
if M[i][j] == 1:
union(i, j, parent)
# 所有节点的都有哪些情况,一种情况代表一个连通分量
for i in parent:
ans.add(find(i, parent))
return len(ans)
a = Solution()
print(a.findCircleNum([[1, 1, 0], [1, 1, 0], [0, 0, 1]]))
优化
以下有部分引用自leetcode
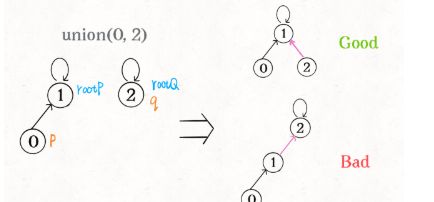
我们一开始就是简单粗暴的把p所在的树接到q所在的树的根节点下面,那么这里就可能出现「头重脚轻」的不平衡状况,比如下面这种局面:
长此以往,树可能生长得很不平衡。我们其实是希望,小一些的树接到大一些的树下面,这样就能避免头重脚轻,更平衡一些。解决方法是额外使用一个size数组,记录每棵树包含的节点数,我们不妨称为「重量」:
比如说size[3] = 5表示,以节点3为根的那棵树,总共有5个节点。
初始化代码优化如下:
parent = defaultdict(int)
size = defaultdict(int) # size用来记录每棵树包含的节点数
for i in range(len(M)):
parent[i] = i
size[i] = 1 # 一开始只有一个节点,因此初始化节点数量为1
优化后的union函数:
def union(x, y, parent,size):
x_root = find(x, parent)
y_root = find(y, parent)
if x_root != y_root:
# 谁的节点数多,谁就做根节点
if size[x_root] > size[y_root]:
parent[y_root] = x_root
size[x_root] += size[y_root]
else:
parent[x_root] = y_root
size[y_root] += size[x_root]
完整代码:
from collections import defaultdict
# 查根
def find(x, parent):
r = x
while r != parent[r]:
r = parent[r]
return r
def union(x, y, parent,size):
x_root = find(x, parent)
y_root = find(y, parent)
# 将x作为根节点
if x_root != y_root:
if size[x_root] > size[y_root]:
parent[y_root] = x_root
size[x_root] += size[y_root]
else:
parent[x_root] = y_root
size[y_root] += size[x_root]
class Solution(object):
def findCircleNum(self, M):
"""
:type M: List[List[int]]
:rtype: int
"""
parent = defaultdict(int)
size = defaultdict(int)
ans = set()
if not M:
return 0
for i in range(len(M)):
parent[i] = i
size[i] = 1
for i in range(len(M)):
for j in range(i, len(M[0])):
if M[i][j] == 1:
union(i, j, parent,size)
for i in parent:
ans.add(find(i, parent))
return len(ans)
a = Solution()
print(a.findCircleNum([[1, 1, 0], [1, 1, 0], [0, 0, 1]]))
总结
1.并查集的思想是很精妙的,用一个数组表示了整片森林(parent)
if M[i][j] == 1:
union(i, j, parent,size)
for i in parent:
ans.add(find(i, parent))
return len(ans)
a = Solution()
print(a.findCircleNum([[1, 1, 0], [1, 1, 0], [0, 0, 1]]))
## 总结
1.并查集的思想是很精妙的,用一个数组表示了整片森林(parent)
2.优化的关键在于记录每棵树的节点数量,让节点数少的森林直线节点数多的森林.