ISP（二） Demosiac 去马赛克 （CIP）

Demosiac是整个ISP imaging pipeline的核心算法，将Bayer pattern的图像转换成RGB。
去马赛克算法是用于从覆盖有颜色滤波器阵列（CFA）的图像传感器输出的不完整颜色样本重建全色图像的数字图像处理。 也称为CFA插值或颜色重建。 重建图像通常在均匀着色的区域中是精确的，但是具有分辨率（细节和清晰度）的损失并且具有边缘伪影。

1. Bayer Pattern

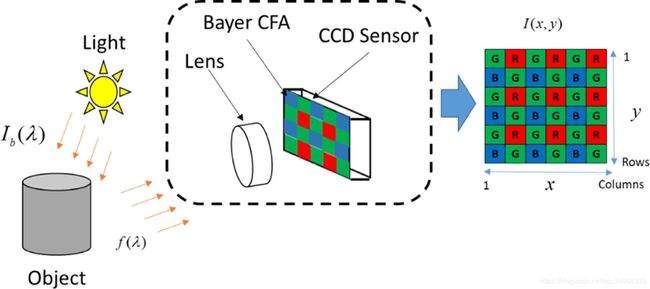
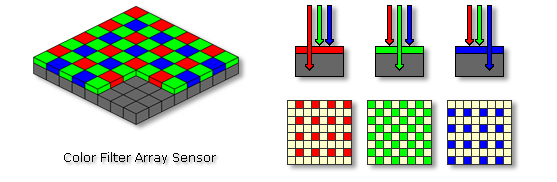
我们知道，CMOS其实只能记录光子的能量，并不能记录光波的波长（即色彩信息），所以，为了得到图像的颜色信息，前人们想到了一种办法，就是在每一个像素面前加带颜色的滤光片，这样就知道某一颜色分量的光强了，柯达的工程师提出了下面这种pattern，也叫CFA（color filter array）。
这样就可以记录色彩信息了，绿色pixel比其他两种颜色多，是因为人眼对绿色(550nm左右)最敏感啊，为什么是这三种颜色呢，三原色呀，那么这样每个像素还是只有一种色彩呀，怎么能得到每个像素的所有色彩呢，插值去马赛克呗
图1
插值，邻域像素的色彩都有了，我们肯定是可以插值出本像素的值的。不过简单的双线性插值的方法总是在IQ上面有缺陷的。在图像的边缘，会产生伪彩色，这一点不难理解。

2. Demosiac CIP的基本方法

demosiac的插值一般遵循以下几个原则：
1.先对G分量进行插值，因为G的像素个数是GB的两倍
2.插值时采用方向性插值，即如果是垂直的边缘，则采用上下的像素进行插值，而不选用左右
3.Hamilton提出的patent奠定了基础，基本原理就是色差恒定，即相邻点的R(i,j)-G(i,j) = R(i, j+1)-G(i, j+1)
A.先获取图像中的物体的边缘
B.根据边缘信息重建G分量
C.根据哈密尔顿提出的色差恒定理论，重建R和B
D.一些后处理，包括伪彩色抑制和zipper cancelling等

3. Nearest Neighbor Replication
每个插值输出像素被分配输入图像中最近像素的值。 最近的邻居可以是上，下，左和右像素中的任何一个。
下面的示例在图2中以绿色平面中的3x3块为例。 在这里，我们假设左侧的相邻像素值用于填充缺失的像素值。

4. Bilinear Interpolation

绿色像素插值：将上，下，左和右像素值的平均值指定为插值像素的G值。 例如：G8 =（G3 + G7 + G9 + G13）/ 4
为方便起见，图1在此重复

红色/蓝色像素的插值：
红色/蓝色像素在绿色位置的插值：将对应颜色的两个相邻像素值的平均值分配给插值像素。 例如：B7 =（B6 + B8）/ 2; R7 =（R2 + R12）/ 2
红色/蓝色像素在蓝色/红色位置的插值：将四个相邻对角像素值的平均值分配给该插值像素。 例如：R8 =（R2 + R4 + R12 + R14）/ 4; B12 =（B6 + B8 + B16 + B18）/ 4

5. Smooth Hue Transition Interpolation 平滑色调过渡插值

双线性插值的关键反对之一是相邻像素的色调不可思议地以不自然的方式改变。 另一方面，拜耳CFA图案可以被认为是由亮度通道（相对多的绿色像素）和色度通道（相对稀疏的红色和蓝色像素）组成。 可以创建一种方案以不同方式内插这些信道。
为方便起见，图1在此重复

绿色像素的插值：
与双线性插值相同。 还要注意绿色像素的插值必须在红/蓝像素的插值之前完成。

红/蓝像素的插值：

这里的想法是尝试从像素到像素强制平滑过渡。
为此，请将蓝色“色调值”定义为：B / G. 并且可以类似地定义红色“色调值”。 考虑蓝色像素值的插值：蓝色像素值插值有三种不同的情况。

估计绿色位置处的蓝色像素值和相邻的蓝色像素位于左侧和右侧：例如， B7 = G7 / 2 *（B6 / G6 + B8 / G8）

估计绿色位置处的蓝色像素值和相邻的蓝色像素位于顶部和底部：例如， B13 = G13 / 2 *（B8 / G8 + B18 / G18）

估计红色位置处的蓝色像素值：例如 B12 = G12 / 4 *（B6 / G6 + B8 / G8 + B16 / G16 + B18 / G18）

6. Edge Sensing Interpolation Algorithm I

非自适应算法，大多数颜色插值是通过不加区分地平均相邻像素来完成的。 这会导致伪影 - 插值图像中的“拉链效果”。 为了对抗这种伪像，很自然地导出一种算法，该算法可以检测像素邻域中存在的局部空间特征，然后有效地选择使用该邻域的预测器。 结果是减少或消除了“拉链型”工件。 涉及这种“智能”检测和决策过程的算法称为自适应颜色插值算法。

人类视觉系统对图像中存在的边缘敏感，并且非自适应颜色插值算法经常在边缘处失败，因为它们不能检测“边缘”。 为了处理边缘，让我们首先看一下边缘感知算法。

绿色像素的插值：
首先，为每个蓝色/红色位置定义两个梯度，一个在水平方向，另一个在垂直方向。 例如，考虑B8：将两个渐变定义为，其中，| | 表示绝对值。
定义一些阈值T.
然后该算法可以描述如下：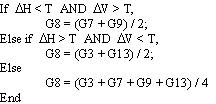
T的选择取决于图像，并且可以具有来自不同邻域的不同最佳值。 T的特定选择是。 在这种情况下，算法变为：![在这里插入图片描述](https://img-blog.csdnimg.cn/20190927165508532.png
红/蓝像素的插值：与对数曝光空间中的平滑色调过渡插值相同。 也可以使用其他方法。

Edge Sensing Interpolation Algorithm II

绿色像素的插值：与边缘感应插值算法I中的相同，不同之处在于不同地定义了horzitonal和垂直渐变。 参考下面的图，为了估算B5处的G5。

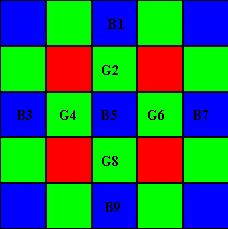
7. Subjective Quality Measure 主观质量测量

Nearest Neighbor Replication Interpolation最近邻复制插值：
整个图像出现明显错误，非常明显的阻塞效果，对于锐边非常不利。静止成像系统不可接受。在视频应用中，许多这些问题可能会被平均掉。

Bilinear Interpolation双线性插值：
与最近邻复制插值相比，性能大大提高;由于平均相邻像素而导致一些模糊;介绍所谓的“拉链”效应

Smooth Hue Algorithms平滑色调算法：
与“宝马”图像中的双线性算法相比，模糊度更低。另一方面，如图像“花朵”中所示，施加了显着的“色调”插值误差。这是由于R / B通道插值中的除法（或对数空间的减法），其中相邻像素之间的大G差异将在插值期间引起巨大的R / B误差。

Edge Sensing Algorithms边缘感应算法：
正如他们的名字所暗示的那样，确实可以看到更清晰的图像。由于R / B插值使用与平滑色调转换算法中相同的算法，因此在图像“鲜花”中可以看到显着的“色调”错误。不太适合彩色小物体。

Linear Interpolation with Laplacian 2nd order color correction terms I 具有拉普拉斯算子的线性插值二阶色彩校正术语I：
在所有算法中给出最佳质量之一。特别适合边缘。

Interpolation using Threshold-based Variable Number of Gradients使用基于阈值的可变梯度数进行插值：
似乎在所有算法中都给出了最佳结果。锋利的边缘也是如此。

Pattern Recognition模式识别：
非常好的结果，但边缘不像可变数字梯度方法或拉普拉斯颜色校正方法那样处理

8. Objective Quality Measure 客观质量测量

为了客观地比较这些算法，我们采用均方误差（MSE）作为我们的质量指标。 原始图像Io（x，y）与每个颜色通道的插值图像Ir（x，y）之间的MSE定义为：

第III节中实现的每种算法的MSE值分别在下面针对三个颜色通道进行描述。 我们将MSE值标准化为最小值，因为我们只关心这些算法的相对性能。

从这些图中，我们得出结论，基于使用MSE的客观测量：

Nearest Neighbor Replication Interpolation 最近邻复制插值比其他算法具有更大的均方误差，因此预期插值图像会显示最差的伪像，这可以在前面的小节中进行验证。

就绿色（或亮度）通道插值而言，Variable Number Gradients Method 可变数梯度方法在两个示例中都提供了最佳性能。 Laplacian Color Correction I method 拉普拉斯颜色校正I方法也给出了令人印象深刻的结果。 就其余算法而言，它们的MSE值没有显示出任何重大差异。

就红/蓝（或色度）通道插值而言，没有明显优越的算法可以单独脱颖而出。Variable Number Gradients Method 变量数梯度方法提供稍好的结果。

9. Computational Cost 计算成本

在这里，我们将比较与实现的每个算法相关的计算成本。我们计算成本的方法是在处理一些输入图像时计算Matlab中发生的触发器。对于那些非自适应算法，只要图像大小是固定的，无论输入图像的内容如何，​​成本都是固定的。而对于自适应算法，计算成本是场景相关的，因为这些算法涉及比较或决策制定步骤，其中可以发生分支。然而，由于图像内容导致的计算成本的这种变化对于我们在此包括的两个示例而言并不明显。
由于计算成本仅从软件的角度来确定，因此它当然与算法的实际实现有关。高效的计划降低了成本。在我们的研究中，没有特别的努力来处理这种与实现相关的成本特征，并且没有一个算法代码被有意调整以提高其效率，也没有故意减少它。我们假设我们的实现行为一般都遵循平均值。
下图显示了两个图像的比较。

Nearest Neighbor Replication Interpolation 最近邻复制插值不涉及任何算术运算，因此不会产生任何计算成本

排除最近邻复制算法，Bilinear interpolation 双线性插值在其他八个插值方案中施加最少量的计算

另一方面，使用interpolation using threshold-based variable number gradients method 基于阈值的可变数梯度方法的插值与其他方法相比具有显着的计算成本代价，并且对于实时数字视频应用来说它是非常不切实际的。

使用Linear interpolation with Laplacian second-order color correction terms I拉普拉斯算子二阶颜色校正项的线性插值与其他算法相比，其也增加了大的计算成本，但与可变数梯度方法相比具有更少的损失。