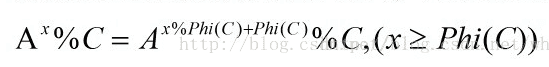数论各种小定理
这里是数论入门题目了 很全面<<– 戳这里
Ax%C=Ax%ϕ(C)+ϕ(C)%C,(x≥ϕ(C))
O(1)解决快速乘取膜
LLu qmodx(LLu a,LLu b,LLu c)
{
a%=c,b%=c;
if(c<=1000000000) return a*b%c;
return (a*b-(LLu)(a/(long double)c*b+1e-8)*c+c)%c;
}n = p1^a1*p2^a2*p3^a3*…*pk^ak 约束和s = (p1^0+p1^1+p1^2+…p1^a1)(p2^0+p2^1+p2^2+…p2^a2)…(pk^0+pk^1+pk^2+…pk^ak)
lucas 定理 快速求大组合数 (省内存&省时间)
组合数求模
组合数求模
#include
#include
#include
#include
#include
using namespace std;
#define lld __int64
lld n, m, p;
lld Ext_gcd(lld a,lld b,lld &x,lld &y)
{
if(b==0) { x=1, y=0; return a; }
lld ret= Ext_gcd(b,a%b,y,x);
y-= a/b*x;
return ret;
}
lld Inv(lld a,int m) ///求逆元
{
lld d,x,y,t= (lld)m;
d= Ext_gcd(a,t,x,y);
if(d==1) return (x%t+t)%t;
return -1;
}
lld Cm(lld n, lld m, lld p) ///组合数学
{
lld a=1, b=1;
if(m>n) return 0;
while(m)
{
a=(a*n)%p;
b=(b*m)%p;
m--;
n--;
}
return (lld)a*Inv(b,p)%p; ///(a/b)%p 等价于 a*(b,p)的逆元
}
int Lucas(lld n, lld m, lld p) ///把n分段递归求解相乘
{
if(m==0) return 1;
return (lld)Cm(n%p,m%p,p)*(lld)Lucas(n/p,m/p,p)%p;
}
int main()
{
int T;
while(~scanf("%I64d%I64d",&n,&m))
{
n--,m--;
m--;
__int64 p=1000000007;
printf("%d\n",Lucas(n+m-1,m,p));
}
return 0;
}
/****************************************/
LL qmul(LL a,LL b,LL c)
{
LL res=0;
while(b)
{
if(b&1) res=(res+a)%c;
a=(a+a)%c;
b>>=1;
}
return res;
}
LL qmod(LL a,LL b,LL c)
{
LL res=1;
while(b)
{
if(b&1) res=qmul(res,a,c)%c;
b>>=1;
a=qmul(a,a,c)%c;
}
return res;
}
LL exgcd(LL a,LL b,LL &x,LL &y) //ax+by=d
{
if(!b)
{
x=1;
y=0;
return a;
}
else
{
LL r=exgcd(b,a%b,x,y);
LL t = x;
x = y;
y=t-a/b*x;
return r;
}
}
LL CRT(LL a[],LL m[],LL len) //x%m[i]=a[i]
{
LL i,x,y,M,n=1,ret=0;
for(i=0; i*=m[i];
for(i=0; i%n;
}
return (ret+n)%n;
}
LL C(LL n,LL m,LL p)//组合数模素数P
{
if(m>n||m<0) return 0;
if(n-m1,b=1;
for(int i=0; i*(n-i)%p;
b=b*(m-i)%p;
}
return a*qmod(b,p-2,p)%p;
}
LL Lucas(LL n,LL m,LL p)
{
LL ans=1;
while(n&&m&&ans)
{
ans=ans*C(n%p,m%p,p)%p;
n/=p,m/=p;
}
return ans;
} 余数问题
这里是余数问题的练习题目
余数定理
计算 (ab)modc 其中b能整除a
如果b与c互素,则 (a/b)%c=a∗bphi(c)−1
如果b与c不互素,则 (a/b)%c=(a%bc)/b
对于b与c互素和不互素都有 (a/b)%c=(a%bc)/b 成立
扩展欧几里得
这里是扩展欧几里德入门的题目了 做完这些我觉得才明白了扩展欧几里德的应用 传送阵<<—
#include 逆元
定义: a×x≡1(modm) ,称x为a关于m的逆元
对于方程 (ax)modc 我们可以转化为求 (a×x−1)modc
由于 x×x−1≡1(modm) 恒成立,所以除法取模就可以将被除数转化为乘上被除数的逆元即可.
求逆元的两种方法
- 扩展欧几里德
(ax)≡?(modc)=>a≡?×x(modc)=>a=?×x+k×c
通过公式的推到,最后得到一个明显的同余式
而?的最小正整数解就是x的逆元
void exgcd(int a,int b,int &d,int &x,int &y){
if(b==0) {
x = 1,y = 0,d=a;
return ;
}
exgcd(b,a%b,d,x,y);
int t = x;
x = y;
y = t - ( a / b ) * y;
return ;
}
int inv(int a){
int x,y,d;
exgcd(a,MOD,d,x,y);
if(d==1) return (x%MOD+MOD)%MOD; //返回最小正整数解
return -1; //不存在逆元
}
/**
注意只有当a与mod互质即 gcd(a,mod) 时才有逆元,否则不存在逆元
*/- 费马小定理
费马小定理 : ap−1≡1(modp) .
可以转化为 a×ap−2≡1(modp) .所以 ap−2 就是a关于p的逆元(!!!!!p必须为素数)
int qmod(int a,int b){
int res = 1;
while(b){
if(b&1) res=res*a%MOD;
b>>=1;
a=a*a%MOD;
}
return res;
}
int inv(int a){
return qmod(a,MOD-2);
}求解高次同余方程
还是用 babystep_gaintstep算法求解。但是这题并不能用POJ_2417的算法,直接套该
算法,下面简要说明一下不能用的原因。首先我们有必要归纳一下用babystep算法解题
的步骤:
(1) 求M = ceil( sqrt(C) ) ;
(2) for(i=0;i< M;i++) hash( i , A^i ) ;
(3) 求D = A^M%C;
(4) r = 1 ; for( i = 0 ; i < M ; i++ ) ex_gcd(r , C , x , y ) ; res = x * B % C ; jj = find( res)
如果找到了这时候的jj,则答案就是i*M+jj,如果没有找到,则res = res * D % C,继续循
环查找,如果最终都没有找到,则输出无解。 在上述的步骤中,如果题目中没有告诉我们
gcd(A , C) = 1,则我们上述的方法是错误的,原因就在于第4步,求res的时候。因为如果
我们无法保证gcd(A , C) = 1 ,也就不能保证gcd(r ,C) = 1(因为D=A^M, r = D^i),所有在
用 扩展欧几里得求出r*x + C*y = gcd(r,C ) 的一个解x0之后,原方程:r*x+C*y = B的解
x = x0 * B / gcd(r,C) + i*C / gcd(r,C) ,但是我们这个时候并不能计算出gcd(r,C),因为此时
的r本来就是经过取余之后得出的,并不能直接用来求gcd,因此我们上述的普通babystep
算法就会出错了。
这样我们就要换一种处理的方法了,这里介绍一种AC大牛博客上的一种“消因子”的方法,
具体内容请看这里:AC大牛。经过上面的分析我们很清楚接下去的处理应该从哪方面着
手,就是应该从不能求出gcd(r , C)入手。一种思想就是既然无法求, 那我每次只要保证
gcd(r, C) = 1那样就可以想普通babystep一样求解了,既然要保证gcd(r,C) =1 ,而
r = (A^M)^i,因此归根到底还是要求gcd( A , C ) = 1。下面就是从AC大牛博客上参考的“消因子”
法了,每次我们 都消去A,C的一个因子,然后对B,C, D进行如下的处理:B/=tmp;C/=tmp ;
D = D* A/tmp%C ,这样经过b轮的消因子之后,gcd(A,C) = 1, 接下去我们就可以用普通
的babystep求解出方程:A^x = B’( mod C’ ) 的解 res1, 原方程的解就是 res = res1 + b。
下面给出这种方法正确的简要证明;一开始我们要求的方程是:A^x = B( mod C ),也就是
求一个最小的x,使得A^x + C*y = B,通过消因子, 我们不断在方程两遍消去gcd(A,C),这
样方程就可以变成 D*A^x1 + C’*y1 = B’,很简单就可以证明上式中 x = x1 + b ; y = y1 的(只要
在方程的两边分别将消去的因子乘回去等式还是保持不变的)。这样我们的问题就转化为了
求x1和y1,即D*A^x1 = B’( mod C’ ),此时gcd( A , C’) = 1,这样我们就可以用普通的babystep
求出上述式子的解x1,同时也就求出了x,这样本题就解决了。
但是上述的方法还是有一个bug的,也就是说,我们用babystep求出的x1>=0,所以上述的
方法只能求出x >= b的解,这样我们自然就会想到如果有一个解x < b怎么办,上述方法就会出
先错误了,因此我们这里还需要改进。考虑b的最大值是多少,考虑每次我们消去的因子数都
最小也就是2,这样我们就可以得到b的最大值就是log(C),这样我们只要保证每次log(C)之内的
解都特判一下, 就不会出现我们刚才的问题了, 所以我们要在进行上述处理之前进行一次for
循环 ,特判0 - log(C)直接的x是否能成为解,接下去再用上述的“消因子”算法。
最后不得不佩服发明这种算法的人的神奇,将O(C)复杂度的判断,分两级判断将复杂度降低
到O( sqrt(C) ),所以就是为什么叫” babystep_gaintstep “了, 哈哈。
babystep算法模板
#define CC(m ,what) memset(m , what , sizeof(m))
LL A, B ,C ;
const int NN = 99991 ;
bool has[NN] ;
int idx[NN] , val[NN] ;
void insert_(int id , LL vv)
{
LL v = vv % NN ;
while( has[v] && val[v]!=vv)
{
v++ ;
if(v == NN) v-=NN ;
}
if( !has[v] )
{
has[v] = 1;
val[v] = vv ;
idx[v] = id ;
}
}
int findi(LL vv)
{
LL v = vv % NN ;
while( has[v] && val[v]!=vv)
{
v++ ;
if(v == NN) v-=NN ;
}
if( !has[v] ) return -1;
return idx[v] ;
}
void ex_gcd(LL a , LL b , LL& x , LL& y)
{
if(b == 0)
{
x = 1 ;
y = 0 ;
return ;
}
ex_gcd(b , a%b , x, y) ;
LL t = x ;
x = y;
y = t - a/b*y ;
}
LL gcd(LL a,LL b)
{
while( a%b != 0)
{
LL c = a ;
a = b ;
b = c % b ;
}
return b ;
}
LL baby_step(LL A, LL B , LL C)
{
LL ans = 1 ;
for(LL i=0; i<=50; i++)
{
if(ans == B) return i ;
ans = ans * A % C ;
}
LL tmp , d = 0 ;
LL D = 1 % C ;
while( (tmp=gcd(A,C)) != 1 )
{
if(B % tmp) return -1 ;
d++ ;
B/=tmp ;
C/=tmp ;
D = D*A/tmp%C ;
}
CC( has , 0) ;
CC( idx, -1) ;
CC(val , -1) ;
LL M = ceil( sqrt(C*1.0) ) ;
LL rr = 1 ;
for(int i=0; i_(i, rr) ;
rr = rr * A % C ;
}
LL x, y ;
for(int i=0; ix, y) ;
LL r = x * B % C;
r = (r % C + C) % C ;
int jj = findi( r ) ;
if(jj != -1)
{
return LL(i)*M + LL(jj) + d ;
}
D = D * rr % C ;
}
return -1 ;
}
素数测试
线性筛法打素数表
int prime[20000],kp=0;
int Is_or[65536];
void Prime()
{
int n =65536; //2~n之间的素数
kp=0;
memset(Is_or,1,sizeof(Is_or));
Is_or[0]=Is_or[1]=0;
for(int i=2;iif(Is_or[i]) prime[kp++]=i;
for(int j=0;j0;
if(i%prime[j]==0) break;
}
}
return ;
} 随机性素数测试 miller-rabbin
普通的素数测试我们有O(√ n)的试除算法。事实上,我们有O(slog³n)的算法。
定理一:假如p是质数,且(a,p)=1,那么a^(p-1)≡1(mod p)。即假如p是质数,且a,p互质,那么a的(p-1)次方除以p的余数恒等于1。(费马小定理)
该定理的逆命题是不一定成立的,但是令人可喜的是大多数情况是成立的。
于是我们就得到了一个定理的直接应用,对于待验证的数p,我们不断取a∈[1,p-1]且a∈Z,验证a^(p-1) mod p是否等于1,不是则p果断不是素数,共取s次。其中a^(p-1) mod p可以通过把p-1写成二进制,由(a*b)mod c=(a mod c)*b mod c,可以在t=log(p-1)的时间内计算出解,如考虑整数相乘的复杂度,则一次计算的总复杂度为log³(p-1)。这个方法叫快速幂取模。
为了提高算法的准确性,我们又有一个可以利用的定理。
定理二:对于0 < x < p,x^2 mod p =1 => x=1或p-1。
我们令p-1=(2^t)*u,即p-1为u二进制表示后面跟t个0。我们先计算出x[0]=a^u mod p ,再平方t次并在每一次模p,每一次的结果记为x[i],最后也可以计算出a^(p-1) mod p。若发现x[i]=1而x[i-1]不等于1也不等于p-1,则发现p果断不是素数。
可以证明,使用以上两个定理以后,检验s次出错的概率至多为2^(-s),所以这个算法是很可靠的。
需要注意的是,为了防止溢出(特别大的数据),a*b mod c 也应用类似快速幂取模的方法计算。当然,数据不是很大就可以免了。
下面是我的程序。
//****************************************************************
// Miller_Rabin 算法进行素数测试
//速度快,而且可以判断 <2^63的数
//****************************************************************
const int S=20;//随机算法判定次数,S越大,判错概率越小
//计算 (a*b)%c. a,b都是long long的数,直接相乘可能溢出的
// a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
a%=c;
b%=c;
long long ret=0;
while(b)
{
if(b&1){ret+=a;ret%=c;}
a<<=1;
if(a>=c)a%=c;
b>>=1;
}
return ret;
}
//计算 x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
if(n==1)return x%mod;
x%=mod;
long long tmp=x;
long long ret=1;
while(n)
{
if(n&1) ret=mult_mod(ret,tmp,mod);
tmp=mult_mod(tmp,tmp,mod);
n>>=1;
}
return ret;
}
//以a为基,n-1=x*2^t a^(n-1)=1(mod n) 验证n是不是合数
//一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
long long ret=pow_mod(a,x,n);
long long last=ret;
for(int i=1;i<=t;i++)
{
ret=mult_mod(ret,ret,n);
if(ret==1&&last!=1&&last!=n-1) return true;//合数
last=ret;
}
if(ret!=1) return true;
return false;
}
// Miller_Rabin()算法素数判定
//是素数返回true.(可能是伪素数,但概率极小)
//合数返回false;
bool Miller_Rabin(long long n)
{
if(n<2)return false;
if(n==2)return true;
if((n&1)==0) return false;//偶数
long long x=n-1;
long long t=0;
while((x&1)==0){x>>=1;t++;}
for(int i=0;ilong long a=rand()%(n-1)+1;//rand()需要stdlib.h头文件
if(check(a,n,x,t))
return false;//合数
}
return true;
}
pollard_rho(longlong质因子分解)
//************************************************
//pollard_rho 算法进行质因数分解
//************************************************
long long factor[100];//质因数分解结果(刚返回时是无序的)
int tol;//质因数的个数。数组小标从0开始
long long gcd(long long a,long long b)
{
if(a==0)return 1;//???????
if(a<0) return gcd(-a,b);
while(b)
{
long long t=a%b;
a=b;
b=t;
}
return a;
}
long long Pollard_rho(long long x,long long c)
{
long long i=1,k=2;
long long x0=rand()%x;
long long y=x0;
while(1)
{
i++;
x0=(mult_mod(x0,x0,x)+c)%x;
long long d=gcd(y-x0,x);
if(d!=1&&d!=x) return d;
if(y==x0) return x;
if(i==k){y=x0;k+=k;}
}
}
//对n进行素因子分解
void findfac(long long n)
{
if(Miller_Rabin(n))//素数
{
factor[tol++]=n; //值得注意的是 这里的factor并不是有序的!!!!!
return;
}
long long p=n;
while(p>=n)p=Pollard_rho(p,rand()%(n-1)+1);
findfac(p);
findfac(n/p);
}
算数基本定理展开
对于任意一个 N 我们可以写成 N=Pa11∗Pa22∗Pa33∗...∗Pann
我们求解的时候只要先讲素数筛出来,然后直接一个个的除就行了,这样的理想复杂度是 O(min{(小于logn2),kp}),kp为筛出的素数个数
但是注意一种情况,可能展开的数N就是一个很大的素数,比如 99997 ,这样的数如果有 1e6 个的话就不能简单快速的展开了.于是我们可以在判定数是否为素数的数组中在开一维记录其为第几个素数.这样一来复杂度就会降低很多 小于O(logn2)
int prime[N],kp;
int Is_or[N][2];
void Prime(){
kp = 0;
memset(Is_or,true,sizeof(Is_or));
Is_or[0][0]=Is_or[1][0]=0;
for(int i=2;i<=100000;i++){
if(Is_or[i][0]) Is_or[i][1]=kp,prime[kp++]=i;//记录其为第几个素数
for(int j=0;j100000;j++){
Is_or[prime[j]*i][0]=0;
if(0==i%prime[j]) break;
}
}
return ;
}
int main(){
int tem;
cin>>tem;
for(int j=0;j=prime[j];j++){
if(Is_or[tem][0]) {a[Is_or[tem][1]]++;break;}
//if(0==tem%prime[j]) ;
while(0==tem%prime[j]) a[j]++,tem/=prime[j];
}
} 乘性函数
欧拉函数表
————————–.
void phi_table() //欧拉函数。。。
{
int i,j;
for(i=2; i<=5e6; i++)
phi[i]=0;
phi[1]=1;
for(i=2; i<=5e6; i++)
if(!phi[i])
for(j=i; j<=5e6; j+=i)
{
if(!phi[j])phi[j]=j;
phi[j]=phi[j]/i*(i-1);
}
phi[0]=0;
return 0;
}
void phi_table(int maxn)
{
for(int i=1;i<=maxn;i++)
phi[i]=i;
for(int i=2;i<=maxn;i+=2)
phi[i]/=2;
for(int i=3;i<=maxn;i+=2)
if(phi[i]==i)
for(int j=i;j<=maxn;j+=i)
phi[j]=phi[j]/i*(i-1);
return ;
}
// 以上是打表的形式 这是求单个的
void Prime()
{
int n=200;
int k=0;
memset(Is_or,1,sizeof(Is_or));
Is_or[0]=Is_or[1]=0;
for(int i=2; iif(Is_or[i])
{
prime[k++]=i;
for(int j=i+i; j0;
}
}
}
return ;
}
LL Phi(LL n)
{
LL rea=n;
for(int i=0; prime[i]*prime[i]<=n&&iif(n%prime[i]==0)
{
rea=rea-rea/prime[i];
while(n%prime[i]==0)
n/=prime[i];
}
}
if(n>1) rea=rea-rea/n;
return rea;
}
/************************/
O(n)求素数+欧拉函数
用最小的素因子筛掉每个数
int prime[N],phi[N],cnt;// prime:记录质数,phi记录欧拉函数
int Min_factor[N];// i的最小素因子
bool vis[N];
void Init()
{
cnt=0;
phi[1]=1;
int x;
for(int i=2;iif(!vis[i])
{
prime[++cnt]=i;
phi[i]=i-1;
Min_factor[i]=i;
}
for(int k=1;k<=cnt&&prime[k]*itrue;
Min_factor[x]=prime[k];
if(i%prime[k]==0)
{
phi[x]=phi[i]*prime[k];
break;
}
else phi[x]=phi[i]*(prime[k]-1);
}
}
} 计算方法
矩阵快速幂
struct Matrix
{
LL m[M][M];
void clearO()
{
for(int i=0; i//初始化矩阵
for(int j=0; j0;
}
void clearE()
{
for(int i=0; i//初始化矩阵
for(int j=0; jvoid display()
{
for(int i=0; ifor(int j=0; jprintf("%d ",m[i][j]);
puts("");
}
}
};
Matrix operator * (Matrix a,Matrix b)
{
Matrix c;
c.clearO();
for(int k=0; kfor(int i=0; i//实现矩阵乘法
{
if(a.m[i][k] <= 0) continue;
for(int j=0; jif(b.m[k][j] <= 0) continue;
c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j]+MOD)%MOD;
}
}
return c;
}
Matrix operator ^ (Matrix a,LL b)
{
Matrix c;
c.clearE();
while(b)
{
if(b&1) c= c * a ;
b >>= 1;
a = a * a ;
}
return c;
}
//#include for(int j=0; jvoid clearO()
{
for(int i=0; ifor(int j=0; j0;
}
void display()
{
for(int i=0; ifor(int j=0; jprintf("%d ",m[i][j]);
puts("");
}
}
};
//循环矩阵 * 的写法。。对于循环矩阵来说 行和列是一样都循环的 并不用特意区分
Matrix operator *(Matrix &a,Matrix &b)
{
Matrix c;
c.row=a.row,c.culumn=b.culumn,c.clearO();
for (int k = 0; k < a.culumn; k++)
if (a.m[0][k])
{
for (int j = 0; j < b.culumn; j++)
if (b.m[k][j])
c.m[0][j] = (c.m[0][j] + a.m[0][k] * b.m[k][j]) % MOD;
}
for (int i = 1; i < c.culumn; i++)
{
c.m[i][0] = c.m[i - 1][c.culumn - 1];
for (int j = 1; j < c.culumn; j++)
c.m[i][j] = c.m[i - 1][j - 1];
}
return c;
}
Matrix operator ^(Matrix &a,int b)
{
Matrix c;
c.row=a.row,c.culumn=a.culumn,c.clearE();
while(b)
{
if(b&1) c=c*a;
b>>=1;
a=a*a;
}
return c;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
LL n,m,L,R,M;
scanf("%I64d%I64d%I64d%I64d%I64d",&n,&m,&L,&R,&M);
MOD=M;
Matrix a,b;
a.row=1,b.row=a.culumn=b.culumn=n,a.clearO(),b.clearO();
for(int i=0; iscanf("%I64d",&a.m[0][i]);
a.m[0][i]%=MOD;
b.m[(i-1+n)%n][i]=R%MOD;
b.m[(i+1)%n][i]=L%MOD;
b.m[i][i]=1;
}
b=b^(m);
a=a*b;
for(int i=0; iif(i)printf(" ");
printf("%I64d",a.m[0][i]);
}
puts("");
}
return 0;
}
FFT/NTT
用于快速求卷积 c=a⊗b
卷积可以类比两个多项式相乘
正常暴力求卷积的复杂度是 O(n2) ,但是通过FFT加速 求卷积的复杂度能降到 O(nlog2n)
算法学习笔记
FFT模板
struct Complex{
double real, image;
Complex(double _real, double _image){
real = _real;
image = _image;
}
Complex(){}
Complex operator + (const Complex &tmp){
return Complex(real + tmp.real, image + tmp.image);
}
Complex operator - (const Complex &tmp){
return Complex(real - tmp.real, image - tmp.image);
}
Complex operator * (const Complex &tmp){
return Complex(real*tmp.real - image*tmp.image, real*tmp.image + image*tmp.real);
}
};
int rev(int id, int len){
int ret = 0;
for(int i = 0; (1 << i) < len; i++){
ret <<= 1;
if(id & (1 << i)) ret |= 1;
}
return ret;
}
Complex A[N];
void FFT(Complex *a, int len, int DFT){
for(int i = 0; i < len; i++)
A[rev(i, len)] = a[i];
for(int s = 1; (1 << s) <= len; s++){
int m = (1 << s);
Complex wm = Complex(cos(DFT*2*PI/m), sin(DFT*2*PI/m));
for(int k = 0; k < len; k += m){
Complex w = Complex(1, 0);
for(int j = 0; j < (m >> 1); j++){
Complex t = w*A[k + j + (m >> 1)];
Complex u = A[k + j];
A[k + j] = u + t;
A[k + j + (m >> 1)] = u - t;
w = w*wm;
}
}
}
if(DFT == -1) for(int i = 0; i < len; i++) A[i].real /= len, A[i].image /= len;
for(int i = 0; i < len; i++) a[i] = A[i];
return;
}
int main()
{
/**
求卷积c=a⊗b
la为a的长度
lb为b的长度
len为最后结果的长度.
**/
int sa,sb;
sa=sb=0;
while((1<(1<int len = (1<<(max(sa,sb)+1));
A = FFT(A,len,1);
B = FFT(B,len,1);
for(int i=0;i<len;i++) A[i]=A[i]*B[i],ans[i]=0;
A = FFT(A,len,-1);
/**
这是最后的卷积的结果.
**/
} NTT
const int Maxn=50000;
LL A[Maxn<<2],B[Maxn<<2];
int ans[Maxn<<2];
inline LL qmod(LL a, LL b,LL P) {
LL ans=1;
for(; b; b>>=1, a=a*a%P)
if(b&1) ans=ans*a%P;
return ans;
}
struct NTT {
int pos[Maxn<<2],k,G,Mod;
inline void init(int len) {
Mod = 998244353,G = 3;
for(k=1; k<=len; k<<=1);
for(int i=1; ipos[i]=(i&1)?((pos[i>>1]>>1)^(k>>1)):(pos[i>>1]>>1);
}
inline void dft(LL *a) {
for(int i=1; iif(pos[i]>i)swap(a[pos[i]],a[i]);
for(int m1=1; m11) {
int m2=m1<<1;
LL wn=qmod(G,(Mod-1)/m2,Mod)%Mod;
for(int i=0; i1;
for(int j=0; j*w%Mod;
B=(A-t+Mod)%Mod;
A=(A+t)%Mod;
w=w*wn%Mod;
}
}
}
}
inline void mui(LL *A,LL *B,int m) {
init(m);
dft(A);dft(B);
for(int i=0; i*B[i]%Mod;
dft(A);
reverse(A+1,A+k);
int inv=qmod(k,Mod-2,Mod)%Mod;
for(int i=0; i*A[i]%Mod;
}
} ntt; 牛顿迭代法 线性开根
下面这种方法可以很有效地求出根号a的近似值:首先随便猜一个近似值x,然后不断令x等于x和a/x的平均数,迭代个六七次后x的值就已经相当精确了。
( 4 + 2/ 4 ) / 2 = 2.25
( 2.25 + 2/ 2.25 ) / 2 = 1.56944..
( 1.56944..+ 2/1.56944..) / 2 = 1.42189..
( 1.42189..+ 2/1.42189..) / 2 = 1.41423..
这种算法的原理很简单,我们仅仅是不断用(x,f(x))的切线来逼近方程x^2-a=0的根。根号a实际上就是x^2-a=0的一个正实根,这个函数的导数是2x。也就是说,函数上任一点(x,f(x))处的切线斜率是2x。那么,x-f(x)/(2x)就是一个比x更接近的近似值。代入f(x)=x^2-a得到x-(x^2-a)/(2x),也就是(x+a/x)/2。
const float EPS = 1e-5;
int sqrt(double x) {
if(x == 0) return 0;
double result = x; /*Use double to avoid possible overflow*/
double lastValue;
do{
lastValue = result;
result = result / 2.0f + x / 2.0f / result;
}while(abs(result - lastValue) > EPS);
return (double)result;
} 更牛逼的一种开跟方式 快的一笔
/**
来自雷神之锤III的源代码中q_math.c的文件中。
*/
float Q_rsqrt( float number ) {
long i; float x2, y; const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
#ifndef Q3_VM #
ifdef __linux__ assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif return y;
}
//整理得到
int sqrt(float x) {
if(x == 0) return 0;
float result = x;
float xhalf = 0.5f*result;
int i = *(int*)&result;
i = 0x5f375a86- (i>>1); // what the fuck?
result = *(float*)&i;
result = result*(1.5f-xhalf*result*result); // Newton step, repeating increases accuracy
result = result*(1.5f-xhalf*result*result);
return 1.0f/result;
} O(n) 预处理逆元
方法一 i的逆元
inv[1] = 1;
for (int i = 2; iMOD%i]*(MOD-MOD/i)%MOD;
方法二 inv{(n-i)!} = inv(n!)*n //阶乘逆元
Fac[0] = 1;
for (int i = 1; i < N; i++) Fac[i] = (Fac[i-1] * i) % MOD;
Inv[N-1] = pow_mod(Fac[N-1], MOD-2);//Fac[N]^{MOD-2}
for (int i = N - 2; i >= 0; i--) Inv[i] = Inv[i+1] * (i + 1) % MOD;
方法三 费马小定理
fac[0]=1;
for(int i=1;i1]*i%MOD;
for(int i=1;iMOD-2); 数学概念
素数
不赘述
反素数
原根
定义:设 m>1 , gcd(a,m)=1 ,使得 ar≡(modm) 成立的最小的 r ,称为 a 对模 m 的阶,记为。 δm(a)
定理:如果模 m 有原根,那么它一共有个 φ(φ(m)) 原根。
定理:若 m>1 , gcd(a,m)=1 , an≡(modm) 则 δm(a)|n 。
定理:如果 p 为素数,那么素数 p 一定存在原根,并且模 p 的原根的个数为 φ(p−1) 。
定理:设 m 是正整数, a 是整数,若 a 模 m 的阶等于 φ(m) ,则称 a 为模 m 的一个原根。
假设一个数 g 对于模 m 来说是原根,那么 gimodp 的结果两两不同,且有 1<g<p , 0≤i<p 那么 g 可以称为是模 p 的一个原根,归根到底就是 gp−1≡(modp) 当且仅当指数为 p−1 的时候成立。(这里是素数)
模 m 有原根的充要条件: m=2,4,pa,2pa ,其中 p 是奇素数。
求模素数 P 原根的方法:对 p−1 素因子分解,即 p−1=pa11pa22...pakk 是的标准分解式,若恒有
gp−1pi≠1(modp)
成立,则 g 就是 p 的原根。(对于合数求原根,只需把 p−1 换成 φ(p) 即可)
求解原根的优化方法
求解原根的完整代码
如果mod 为素数
int get(int mod) {
for(int i = 2; ; i++) {
set<int> s;
for(int j = 1, x = 1; j < mod; j++) {
x = (x*i)%mod;
s.insert(x);
}
if(s.size() == mod-1) return i;
}
}
----------------------------------------------------------------
//注意爆int,所以用LL
LL qmod(LL a,LL b,LL c){
LL res = 1;a%=c;
while(b){
if(b&1) res=res*a%c;
b>>=1,a=a*a%c;
}
return res;
}
int prime[N];
int Is_or[N][2];
void Prime(){
int n = 100000;
prime[0]=0;
memset(Is_or,1,sizeof(Is_or));
for(int i=2;i<=n;i++){
if(Is_or[i][0]) prime[++prime[0]]=i,Is_or[i][1]=prime[0];
for(int j=1;j<=prime[0]&&i*prime[j]<=n;j++){
Is_or[i*prime[j]][0]=0;
if(0==i%prime[j]) break;
}
}
return ;
}
int Phi(int x){
//因为本题中数据都是质数,所以欧拉函数值就都是x-1了。
return x-1;
}
int a[10000],cnt;
void divide(int n){
cnt = 0;
for(int i=1;prime[i]*prime[i]<=n;i++){
if(n<=prime[prime[0]]&&Is_or[n][0]){a[++cnt]=n;n=1;break;}
if(n%prime[i]==0){a[++cnt]=prime[i];n/=prime[i];}
while(n%prime[i]==0){n/=prime[i];}
}
if(n>1)a[++cnt]=n;
return;
}
void work(int n){
int phi = Phi(n);
bool flag ;
for(int i=2;i//一个数的原根是很小的 所以暴力枚举就行,但其实是有优化方法的,
flag = true;
for(int j=1;j<=cnt;j++){
int tmp = phi/a[j];
if(qmod(i,tmp,n)==1){
flag = false;
break;
}
}
if(flag){
printf("%d\n",i);
return ;
}
}
puts("没有原根");
}
int main(){
Prime();
int n;
while(~scanf("%d",&n)){
divide(Phi(n));
work(n);
}
return 0;
}