《GA-Net: Guided Aggregation Net for End-to-end Stereo Matching》笔记
GA-Net
《GA-Net: Guided Aggregation Net for End-to-end Stereo Matching》
CVPR2019的一篇双目匹配论文,借鉴了一些传统方法SGM和滤波的思想,提出了两个网络层。
论文:https://arxiv.org/pdf/1904.06587v1.pd
代码:https://github.com/feihuzhang/GANet
一、摘要
在双目匹配任务里,传统方法和深度学习方法里代价聚合都非常重要,可以获得更准确的视差。提出了两个新的网络层分别来获取局部和全局的代价依赖关系;
SGA(半全局聚合层):SGM算法的可微近似,提高遮挡区域、大的无纹理区域和反光区域(玻璃等);
LGA(局部指导聚合层):借鉴传统方法里的代价滤波策略,处理薄结构和物体边缘,弥补下采样和上采样的细节损失;
一个GA层相当于3D卷积层1/100的计算量,速度15-20fps,可以直接把这两层来替换常用的3D卷积,参数会少很多;
设计了一引导聚合网络GA-Net;
Scene Flow和KITTI上达到最佳效果。
二、相关工作
1.局部代价聚合:
匹配代价C是由每个像素在每个候选视差值d的地方计算来的代价,形状是 H ∗ W ∗ D m a x H * W * D_{max} H∗W∗Dmax , 可以按照 D D D 来划分成 D m a x D_{max} Dmax 个切片。局部代价过滤的方法比较高效,对每一个像素 p = ( x , y ) p=(x,y) p=(x,y)在视差为d时候的代价为相同切片里周围像素的加权平均。
公式:
C A ( p , d ) = ∑ q ∈ N p ω ( p , q ) . C ( q , d ) C^A(p,d)=\sum_{q\in{N_p}}\omega(p,q).C(q,d) CA(p,d)=q∈Np∑ω(p,q).C(q,d)
C ( q , d ) C(q,d) C(q,d):位置 p p p 处候选视差为 d d d 时候的代价值;
C A ( p , d ) C^A(p,d) CA(p,d) :局部聚合之后的代价。
有很多图像滤波方法都可以用到生成指导过滤的权重 ω \omega ω,局部聚合方法很快,可以达到实时。
2.半全局匹配:
半全局聚合方法,匹配代价和平滑性约束都被包含在一个能量函数 E ( D ) E(D) E(D) 里, 问题是如何找到一个视差图 D ∗ D^* D∗可以让 E ( D ) E(D) E(D) 最小。
E ( D ) = ∑ p { C p ( D p ) + ∑ q ∈ N p P 1 . δ ( ∣ D p − D q ∣ = 1 ) + ∑ q ∈ N p P 2 . δ ( ∣ D p − D q ∣ > 1 ) } E(D)=\sum_p \{C_p(D_p) + \sum_{q \in N_p}P_1.\delta(|D_p-D_q|=1)+\sum_{q \in N_p}P_2.\delta(|D_p-D_q|>1)\} E(D)=∑p{Cp(Dp)+∑q∈NpP1.δ(∣Dp−Dq∣=1)+∑q∈NpP2.δ(∣Dp−Dq∣>1)}
其中:
1) ∑ p C p ( D p ) \sum_p C_p(D_p) ∑pCp(Dp) 是所有像素位置p的代价和;
2) P 1 P1 P1 是对像素 p p p 的所有邻域像素 q q q的常数惩罚,如果它们在视差图上有小的不连续(视差相差为1);
3) P 2 P2 P2 是较大的惩罚,针对邻域视差和 p p p 点视差相差大的时候(>1).
SGM从16个方向进行1维代价聚合,当方向为 r r r 且候选视差为 d d d时的代价 C r A ( p , d ) C_r^A(p,d) CrA(p,d)聚合整合1维路径上的代价,定义为:
C r A ( p , d ) = C ( p , d ) + m i n { C r A ( p − r , d ) , C r A ( p − r , d − 1 ) + P 1 , C r A ( p − r , d + 1 ) + P 1 , m i n i C r A ( p − r , i ) + P 2 , C^A_r(p,d)=C(p,d)+min \begin{cases} C^A_r(p-r,d),\\ C^A_r(p-r,d-1)+P_1, \\ C^A_r(p-r,d+1)+P_1,\\ min_i{C^A_r(p-r,i)}+P_2,\\ \end{cases} CrA(p,d)=C(p,d)+min⎩⎪⎪⎪⎨⎪⎪⎪⎧CrA(p−r,d),CrA(p−r,d−1)+P1,CrA(p−r,d+1)+P1,miniCrA(p−r,i)+P2,
其中:
1) C ( p , d ) C(p,d) C(p,d) 是当前位置p在视差为d时候的代价;
2) C r A ( p − r , d ) 、 C r A ( p − r , d − 1 ) 、 C r A ( p − r , d + 1 ) C^A_r(p-r,d)、C^A_r(p-r,d-1)、C^A_r(p-r,d+1) CrA(p−r,d)、CrA(p−r,d−1)、CrA(p−r,d+1)是在当前方向 r r r =上视差为 d 、 d − 1 、 d + 1 d、d-1、d+1 d、d−1、d+1 时的代价;
3) m i n i C r A ( p − r , i ) min_i{C^A_r(p-r,i)} miniCrA(p−r,i) 是当前路径任意视差时的最小代价;
4) P 1 、 P 2 P1、P2 P1、P2是惩罚值。
三、Guided Aggregation Net
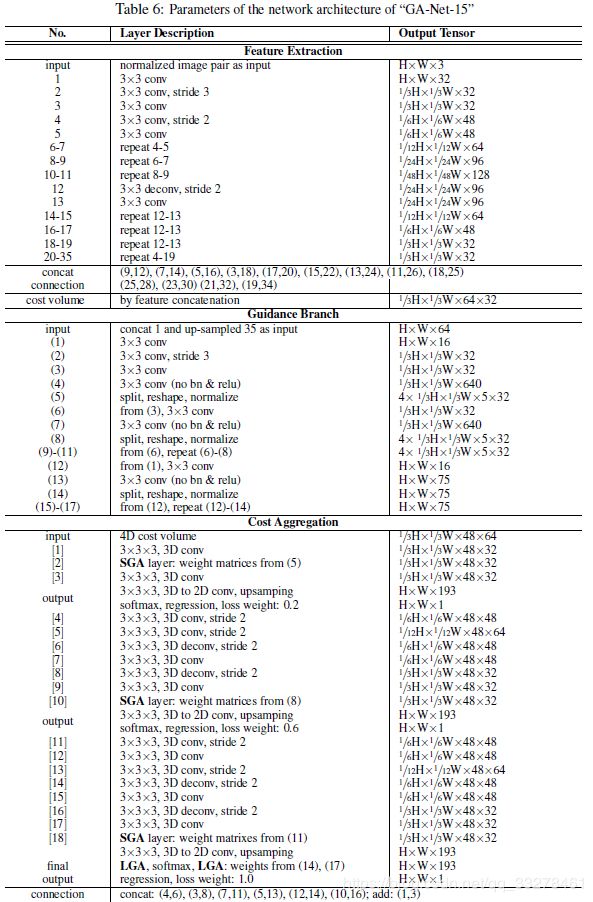
PSMNET,GCNET这些目前最好双目匹配网络都是通过叠加双目图像特征构造4D的匹配代价 ( H ∗ W ∗ D m a x ∗ F ) (H*W*D_{max}*F) (H∗W∗Dmax∗F),其中 F F F 是特征的大小,下一步就是代价聚合,最后是视差估计。GA-Net用的是SGA和LGA。
3.1 SGA
传统的SGM算法从各个方向迭代聚合匹配代价,是不可微的难以端到端训练神经网络。
3.1.1 直接用SGM会出现一些问题?
1)很多需要用户设置的参数(如 P 1 , P 2 P_1,P_2 P1,P2 )不能直接设置,会导致神经网络训练不稳定。
2)SGM的代价聚合和惩罚针对所有像素区域是固定的,没有根据环境变化自适应。
3)直接选择最小代价会导致视差估计时正面出现一些平行表面,属于hard操作。
3.1.2 针对以上问题修改后的SGM?
C r A ( p , d ) = C ( p , d ) + s u m { w 1 ( p , q ) . C r A ( p − r , d ) , w 2 ( p , q ) . C r A ( p − r , d − 1 ) , w 3 ( p , q ) . C r A ( p − r , d + 1 ) , w 4 ( p , r ) . m a x i C r A ( p − r , i ) . C^A_r(p,d)=C(p,d)+sum \begin{cases} w_1(p,q).C^A_r(p-r,d),\\ w_2(p,q).C^A_r(p-r,d-1),\\ w_3(p,q).C^A_r(p-r,d+1),\\ w_4(p,r).{max}_{i}C^A_r(p-r,i). \end{cases} CrA(p,d)=C(p,d)+sum⎩⎪⎪⎪⎨⎪⎪⎪⎧w1(p,q).CrA(p−r,d),w2(p,q).CrA(p−r,d−1),w3(p,q).CrA(p−r,d+1),w4(p,r).maxiCrA(p−r,i).
1)用户定义参数变为可学习参数,修改成了惩罚系数,可以更适应位置变化。
2)把外层的选择最小值改成了求和(没有损失精度),最大池化换成了步长卷积。
3)把内层的选择最小值改成了求最大值,因为现在的学习目标是最大化正确深度的概率而不是最小化代价。
3.1.3 防止代价越来越大继续修改SGM?
C r A ( p , d ) C_r^A(p,d) CrA(p,d) 在一条路径上会变的很大,SGM处理方法是减去一个值,这里把各项权重归一化处理:
公式如下:
C r A ( p , d ) = s u m { w 0 ( p , r ) . C ( p , d ) , w 1 ( p , q ) . C r A ( p − r , d ) , w 2 ( p , q ) . C r A ( p − r , d − 1 ) , w 3 ( p , q ) . C r A ( p − r , d + 1 ) , w 4 ( p , r ) . m a x i C r A ( p − r , i ) . C^A_r(p,d)=sum \begin{cases} w_0(p,r).C(p,d),\\ w_1(p,q).C^A_r(p-r,d),\\ w_2(p,q).C^A_r(p-r,d-1),\\ w_3(p,q).C^A_r(p-r,d+1),\\ w_4(p,r).{max}_{i}C^A_r(p-r,i). \end{cases} CrA(p,d)=sum⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧w0(p,r).C(p,d),w1(p,q).CrA(p−r,d),w2(p,q).CrA(p−r,d−1),w3(p,q).CrA(p−r,d+1),w4(p,r).maxiCrA(p−r,i).
s . t . ∑ i = 0 , 1 , 2 , 3 , 4 w i ( p , r ) = 1 s.t. \sum_{i=0,1,2,3,4}w_i(p,r)=1 s.t.i=0,1,2,3,4∑wi(p,r)=1
这里是4个方向而不是SGM的16个方向, w 0 , w 1 , w 2 , w 3 , w 4 w_0,w_1,w_2,w_3,w_4 w0,w1,w2,w3,w4 对所有视差切片共享;
3.4.4 如何选择聚合值?
最后的聚合值 C A ( p ) C^A(p) CA(p) 是选择的四个方向最大的:
C A ( p , d ) = m a x r C r A ( p , d ) C^A(p,d)=max_rC_r^A(p,d) CA(p,d)=maxrCrA(p,d)
最大值保留了最佳信息,保证聚合值不被其他方向模糊。
3.2 LGA
双目匹配里广泛使用的上采样和下采样会让薄结构和边界模糊,LGA通过学习几个指导滤波器来细化匹配代价,恢复薄结构信息。
3.2.1 代价过滤器定义为:
C A ( p , d ) = s u m { ∑ q ∈ N p ω 0 ( p , q ) . C ( q , d ) , ∑ q ∈ N p ω 1 ( p , q ) . C ( q , d − 1 ) , ∑ q ∈ N p ω 2 ( p , q ) . C ( q , d + 1 ) . C^A(p,d)=sum \begin{cases} \sum_{q \in N_p}\omega_0(p,q).C(q,d),\\ \sum_{q \in N_p}\omega_1(p,q).C(q,d-1),\\ \sum_{q \in N_p}\omega_2(p,q).C(q,d+1). \end{cases} CA(p,d)=sum⎩⎪⎨⎪⎧∑q∈Npω0(p,q).C(q,d),∑q∈Npω1(p,q).C(q,d−1),∑q∈Npω2(p,q).C(q,d+1).
s . t . ∑ q ∈ N p ω 0 ( p , q ) + ω 1 ( p , q ) + ω 2 ( p , 1 ) = 1 s.t. \sum_{q \in N_p}\omega_0(p,q)+\omega1(p,q)+\omega_2(p,1)=1 s.t.q∈Np∑ω0(p,q)+ω1(p,q)+ω2(p,1)=1
3.2.2 和传统过滤方法的区别?
匹配代价的不同切片(一共 D m a x D_{max} Dmax个切片)共享权重,但是传统代价过滤算法只用一个 K ∗ K K*K K∗K的过滤核来过滤邻域的代价,LGA是用3个 K ∗ K K*K K∗K的过滤器( ω 0 , ω 1 , ω 2 \omega_0,\omega_1,\omega_2 ω0,ω1,ω2)过滤像素 p p p在视差 d , d − 1 , d + 1 d,d-1,d+1 d,d−1,d+1时候的代价。用 K ∗ K ∗ 3 K*K*3 K∗K∗3 的矩阵在 K ∗ K K*K K∗K 区域聚合,针对的是每一个像素位置p的局部区域。
四、高效实现
匹配代价形状 H ∗ W ∗ D ∗ F H*W*D*F H∗W∗D∗F,F是特征大小,引导子网的输出是 H ∗ W ∗ K ∗ F ( K = 5 ) H*W*K*F(K=5) H∗W∗K∗F(K=5),四个方向在一个切片d上共享聚合参数。
LGA权重矩阵 H ∗ W ∗ 3 K 2 ∗ F ( K = 5 ) H*W*3K^2*F(K=5) H∗W∗3K2∗F(K=5)。SGA和LGA都可以并行进行计算。为了增加LGA的感受野用相同参数矩阵计算两次。
五、网络结构
5.1 网络四个部分
特征抽取模块:左右图共享权值抽取特征,堆叠的沙漏结构(PSM用的也是)最后输出4D代价;
代价聚合模块:几个SGA和LGA层;
引导子网:几个2D卷积层,输出reshape为SGA和LGA权重的形状;
视差回归:用softmax层和回归层;
5.2 和PSMNET、GCNET等的区别?
主要是代价聚合的地方不是纯堆叠3D卷积,用引导子网生成权重来做SGA和LGA。
六、Loss函数
用smooth L1,相比L2在视差不连续处更鲁棒,对离群点和噪声不敏感。
6.1 损失公式:
L ( d ^ , d ) = 1 N ∑ n = 1 N l ( ∣ d ^ − d ∣ ) L(\hat{d}, d)=\frac{1}{N} \sum_{n=1}^{N} l(|\hat{d}-d|) L(d^,d)=N1n=1∑Nl(∣d^−d∣)
l ( x ) = . { x − 0.5 , x > = 1 x 2 / 2 , x < 1 l(x)=. \begin{cases} x-0.5,x>=1 \\ x^2/2, x<1 \end{cases} l(x)=.{x−0.5,x>=1x2/2,x<1
∣ d ^ − d ∣ |\hat d - d| ∣d^−d∣ :预测视差和真值的绝对值误差;
N:有效像素总数,根据真值看是否有效。
6.2 怎么做视差估计:
d ^ = ∑ d = 0 D m a x d ∗ σ ( − C A ( d ) ) \hat d = \sum_{d=0}^{D_{max}} d* \sigma(-C^A(d)) d^=d=0∑Dmaxd∗σ(−CA(d))
σ \sigma σ是softmax操作,对代价聚合后的代价softmax找到每个视差d的概率,然后对所有候选视差加权求和作为某位置最终视差。这样做比直接分类更鲁棒。
七、实验
Adam( β 1 = 0.9 , β 2 = 0.999 \beta1=0.9, \beta2=0.999 β1=0.9,β2=0.999)、batch_size=16(8个GPU),random crop(240 * 576),maxidsparity=192;
对所有图像通道减均值除标准差;
ScenceFlow数据集训练10个epochs,学习率0.001;
KITTI数据集在ScenceFlow预训练模型上继续训练640个epochs,前300个学习率0.001,后300个学习率0.0001。
7.1 GA层的实验
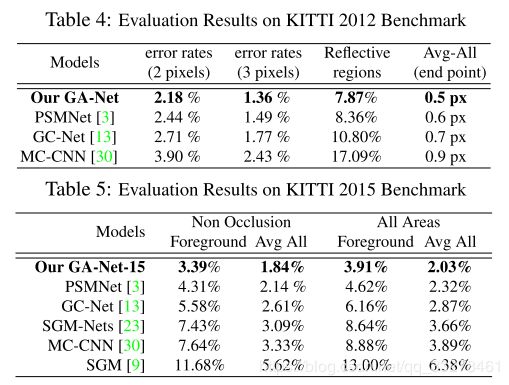
结论:3个SGA和1个LGA层在ScenceFlow和KITTI都达到最佳,ScenceFlow的逐点误差EPE为0.84,预测结果相差一个像素的为9.9%,KITTI相差一个像素的为2.71%。
结论: GA层对EPE平均提升0.5-1.0像素
-
代价聚合方法对比

实验固定特征抽取部分,
GA-Net-2:2个GA层+3个3D卷积的GA-Net超过了GCNET;
GA-Net-7:3个GA层+7个3D卷积的GA-Net超过了PSMNET;
结论:GA-Net参数少,精度高,几层3D卷积就可以达到很高的精度。 -
softmax后的不同视差值的概率分布
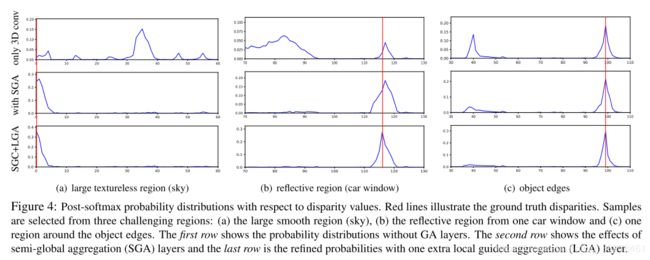
结论:
带SGA和LGA的模型针对大的无纹理区域、反射区域、目标边界三种困难情况效果都更;
| 区域 | 问题 | GA层效果 |
|---|---|---|
| 无纹理区域 | 没有有分辨性的特征,所以噪声多 | SGA 用周围信息抑制噪声,LGA更关注真值处的峰值,可以细化结果 |
| 反射区域 | 亮度,光滑表面影响,出现一些错误匹配 | 修正错误视差匹配,更关注真值处的峰值 |
| 目标边界 | 容易被周围背景影响导致边界模糊 | 选择最大的空间聚合结果,有效的去除来自背景的错误匹配信息 |
7.2 GA层和3D卷积对比
7.2.1 SGA相比SGM的改变?
SGA是SGM近似可微表示;
1)无需用户定义参数(P1,P2),端到端学习参数;
2)聚合方式由权重矩阵控制,引导子网学习几何和上下文信息来控制聚合的方向、范围和强度;
7.2.2 SGA在无纹理区域为什么比SGM更好?
SGA在大无纹理区域中避免了大多数的正面平行近似。
原因可能是:
1)不选最大或最小值,而用加权求和(更soft);
2)回归损失比分类损失鲁棒;
9)有助于达到亚像素精度。
7.2.3 SGA和3D卷积比?
SGA更高效。
3D卷积是所有局部位置共享卷积核,必须要很多层才有好结果;
SGA一层就可以聚合半全局的信息,并且聚合方向、范围、强度都根据位置变化(不同几何和上下文信息)得到不同权重。
比如:SGA在遮挡和大的光滑处处理方式不同,而3D卷积在全图都进行相同处理。
- 最好的模型和经典模型对比
八. 推导
九、总结
提出了SGA和LGA层,可以替换常用的3D卷积代价聚合方式,更高效更快速。
虽然SGM也被引入到深度学习里,LGA的过滤方法也很多,估计很多人想过弄个类似的(global+local)方法,但是作者把他弄出来了,并且做了实验证实确实不错,挺不错的工作,算是比较靠谱的文章。
论文涉及到了SGM、SGM-NET和滤波相关内容可以简单看看也。