AMCL算法原理讲解

AMCL算法理解

AMCL(adaptive Monte Carlo Localization)自适应蒙特卡洛定位 ，源于MCL算法的一种增强，那么为什么要从MCL升级为AMCL呢？首先应该了解MCL的算法原理

本教程是对Dr. Sebastian Thrun所著《概率机器人》（Probabilistic Robotics）一书的部分原理讲解，插图均来自该书，如有兴趣深入理解请大家购买原书进行学习

蒙特卡洛定位算法

蒙特卡洛定位适用于局部定位和全局定位两类问题，尽管它相对的年轻，但是已经成为定位领域中的主流算法，如下所示为蒙特卡洛定位算法：

通过把合适的概率运动和感知模型代入到粒子滤波算法中得到，使用M个粒子的集合 ${\chi }_t=\{x_t^{[1]},x_t^{[2]},...,x_t^{[M]}\}$表示置信度$bel(x_t)$，初始置信度由先验分布随机产生的M个这样的粒子得到。算法第4行使用运动模型采样，以当前置信度为起点使用粒子，第5行使用测量模型以确定粒子的重要性权值（这两个模型介绍见第二、三节）通过增加粒子总数M能提高定位的近似精度。
MCL以目前的形式解决了全局定位问题，但无法从机器人绑架或全局定位失败中恢复过来。当机器人位置被获取时，其他地方的不正确粒子会逐渐消失。在某种程度上，粒子只能“幸存”在一个单一的姿势附近，如果这个姿势恰好不正确，算法就无法恢复。而这个问题可通过相当简单的探索算法解决，其思想是增加随机粒子到粒子集合，从而在运动模型中产生一些随机状态，这便是AMCL算法的由来。

蒙特卡洛定位算法自适应变种

AMCL算法在机器人遭到绑架的时候，会随机注入粒子（injection of random particles），增加粒子的方法引起两个问题，一是每次算法迭代中应该增加多少粒子，二是从那种分布产生这些粒子。
解决第一个问题可通过监控传感器测量的概率来评估增加粒子，即式$(1.1)$
$$p(z_t|z_{1:t-1},u_{1:t},m)$$
并将其与平均测量概率联系起来，在粒子滤波中这个数量的近似容易根据重要性因子获取，因为重要性权重是这个概率的随机估计，其平均值为式$(1.2)$
$$\frac{1}{M}\sum _{m=1}^M{w}_t^{[m]}\approx p(z_t|z_{1:t-1},u_{1:t},m)$$
这个接近上式中的期望概率。
解决第二个问题可以根据均匀分布在位姿空间产生粒子，用当前观测值加权得到这些粒子。如下给出增加随机粒子的蒙特卡洛定位算法自适应变种（AMCL）：

与MCL相比，这个算法跟踪式$(1.1)$的似然值的短期与长期均值，整体框架与MCL相同，但在第八行中给出了经验测量似然，并在第10、11行维持短期和长期似然平均，算法要求$0\le {\alpha }_{slow}\le {\alpha }_{fast}$ ，参数α_slow和α_fast分别估计长期和短期平均的指数滤波器的衰减率。算法的关键在第13行，重采样过程中，随机采样以以下式$(1.3)$概率增加
$$max\{0.0,1-\frac{w_{fast}}{w_{slow}}\}$$
否则重采样以MCL相同的方式进行，即根据式$(1.3)$如果短期似然优于长期似然，则算法将判断不增加随机采样，否则的话则按两者之比的比例增加随机采样，以这种方式可抵消瞬时传感器噪声带来的定位误差。

里程计运动模型

在第一章MCL和AMCL算法中均涉及运动模型采样，本章将介绍所使用的里程计运动模型。里程通常可通过整合轮子的编码信息来得到，许多商业机器人在固定的时间间隔产生这样的积分位姿估计，即里程计运动模型通过距离测量来估计运动。
解决机器人定位问题主要是解决从机器人内部里程计使用的坐标到物理世界坐标之间的变换问题。里程计模型使用相对运动信息，由内部里程计测量，在时间间隔$(t-1,t]$内，机器人从位姿x_t-1运动到x_t，里程计反馈了从${\bar{x}}_{t-1}=(\bar{x}\bar{y}\bar{\theta }{)}^T$到${\bar{x}}_t=(\overline{x^{\prime }}\overline{y^{\prime }}\overline{{\theta }^{\prime }}{)}^T$的相对前进，这里的‘-’代表其是基于机器人内部坐标的，该坐标系与全局世界坐标的关系是未知的。在状态估计中利用${\bar{x}}_{t-1}$和${\bar{x}}_t$之间的相对差是真是位姿x_t-1和x_t之间差异的一个很好的估计器，因此运动信息u_t由下式$(2.1)$给出：
$$u_t=\left(\genfrac{}{}{0ex}{}{{\bar{x}}_{t-1}}{{\bar{x}}_t}\right)$$
为了提取相对距离，u_t被转变成三个步骤：旋转${\delta }_{rot1}$、直线平移${\delta }_{trans}$和另一个旋转${\delta }_{rot2}$，如下图所示：

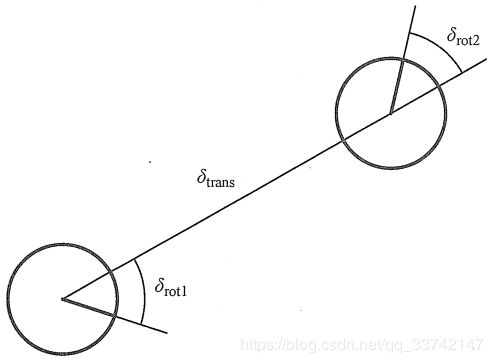
这三个参数足以组成由历程及编码的相对运动的统计量。由于AMCL是基于粒子滤波的定位方法，因此希望有一个$p(x_t|u_t,x_{t-1})$的采样算法，运动模型采样算法如下所示：

从算法2. 1中我们可以看到，四个$\alpha$参数分别对旋转和平移方向的撒点角度$\delta$产生影响，使用采样算法可直接通过控制得到位姿估计x_t的值。

测距仪模型

与里程计运动模型相同，在第一章MCL和AMCL算法中均涉及了使用测量模型确定离子的重要性权值，测距仪是时下最流行的机器人传感器，因此使用测距仪作为测量模型的近似物理模型来测量附近物体的距离。

波束模型

波束模型采用四类测量误差，包括小的测量噪声、意外对象引起的误差、由于未检测到对象引起的误差和随机意外噪声。因此期望模型$p(z_t|x_t,m)$是四个密度的混合，每一种密度都与一个特定类型的误差有关，四种密度如下所示：

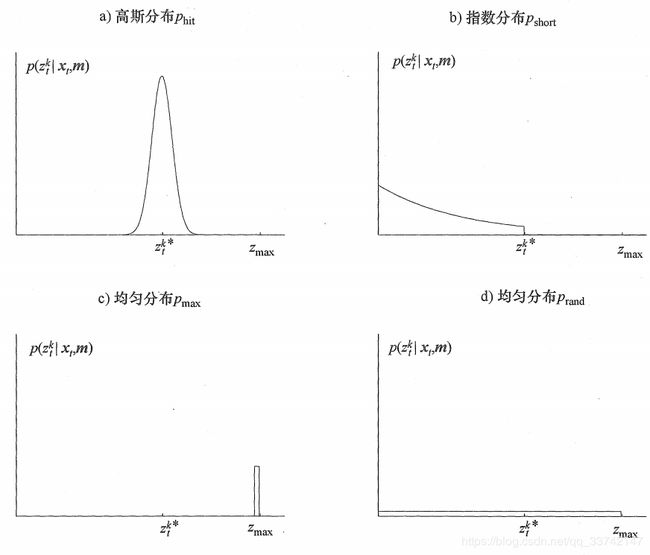
1. 即使传感器正确测量了最近对象的距离，它返回的值也受到误差的影响，即测量噪声，通常由一个窄的均值为$z_t^{k\ast }$、标准偏差为${\sigma }_{hit}$的高斯建模，p_hit表示高斯分布，如上图a)所示，实际上测距传感器的值局限于区间$[0;z_{max}]$，这里$z_{max}$表示最大的传感器距离。
2. 意外对象比如与机器人共享操作空间的人，处理这类对象的一种方法是将他们作为传感器噪声来处理，未建模对象会导致比$z_t^{k\ast }$更短的距离。该情况下距离测量用指数分布描述，如上图b)，其密度在$z_t^k$范围内指数减少。
3. 有时环境中的障碍会被完全忽略如声呐传感器遇到镜面反射、激光雷达检测到黑色吸光物体等，这便是传感器检测失败误差，其典型结果是返回传感器允许的最大值$z_{max}$，这是一个离散函数，如上图c)所示。
4. 测距仪偶尔会产生完全无法解释的测量，例如超声在几面墙之间反弹，从而产生随机意外噪声，为了使之简单化，对于这样的测量，这里使用一个分布在完整传感器测量范围$[0;z_{max}]$的均匀分布来建立模型。如上图d)所示。

上述4个参数$z_{hit},z_{short},z_{max},z_{rand}$通过加权平均混合，且有
$$z_{hit}+z_{short}+z_{max}+z_{rand}=1$$
注意此处的$z_{max}$只是一个参数而与前文所提最大传感器距离$z_{max}$不同，所有4种密度线性组合后得到的典型密度如下图所示：

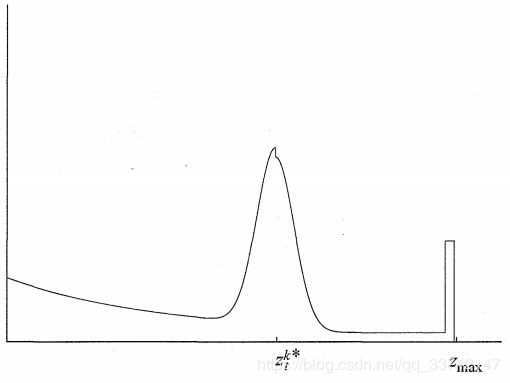
可以看到所有4种基本模型的基本特性在这个组合密度中仍然存在，故测距仪模型可由如下波束模型算法实现：

其中算法的输入包括一个完整的距离扫描$z_t$、机器人姿态$x_t$和地图$m$，在一个循环中将各传感器波束$z_t^k$的似然相乘，第4行采用射线投射来特定的传感器测量计算无噪声距离，第5行计算了各个距离测量的似然，算法返回期望的概率$p(z_t^k|x_t,m)$。
基于波束的传感器模型具有两个主要缺点，一是缺乏光滑性，在有许多小障碍的混乱环境中分布不光滑，二是计算量过大，因为该模型需要对每一个传感器的波束都进行评估，故计算量过大需要很大内存。为了克服以上缺点，引入另一种似然域模型。

似然域模型

似然域模型不必计算相对于任何有意义的传感器物理生成模型的条件概率，因为该模型没有一个合理的物理解释。它的主要思想是首先将传感器扫描的终点$z_t$映射到地图的全局坐标空间，因此就必须知道机器人的局部坐标系在何处、传感器光束的源头和指向等信息。
机器人$t$时刻的位姿为$x_t=(x,y,\theta {)}^T$，传感器的安装位置相对于机器人的中心坐标$(x_{k,sense},y_{k,sense}{)}^T$,激光光束相对于机器人的朝向角度为${\theta }_{k,sense}$,激光测量的终点相对传感器中心为$z_t^k$，激光扫描到的点投影到地图的全局坐标系坐标为$(x_{z_t^k},y_{z_t^k}{)}^T$,其坐标变化如下式$(3.1)$所示
$$\begin{gathered} \left(\genfrac{}{}{0ex}{}{x_{z_t^k}}{y_{z_t^k}}\right)=\left(\genfrac{}{}{0ex}{}{x}{y}\right)+\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\genfrac{}{}{0ex}{}{x_{k,sense}}{y_{k,sense}}\right) \\ +z_t^k\left(\genfrac{}{}{0ex}{}{cos(\theta +{\theta }_{k,sense})}{sin(\theta +{\theta }_{k,sense})}\right) \end{gathered}$$
这些坐标只有当传感器监测到障碍物才有意义，否则会输出最大值$z_{max}$，而在似然域模型中将会把最大距离的读数丢弃。
与波束模型类似，似然域模型有三种噪声和不确定性来源，分别是测量噪声、测量失败和无法解释的随机测量，其中测量噪声涉及寻找地图上最近的障碍物，其高斯噪声与测量目标到地图$m$上最近物体之间的欧氏距离有关，与基于波束模型的传感器模型相同，期望概率$p(z_t^k|x_t,m)$集成了所有三种分布$z_{hit}{p}_{hit}+z_{rand}{p}_{rand}+z_{max}{p}_{max}$，式中使用熟悉的混合权值$z_{hit}、z_{rand}和z_{max}$。其算法如下所示：

与波束算法类似，该算法通过循环将各个$p(z_t^k|x_t,m)$的值相乘，并假定不同传感器波束的噪声相互独立，第4行判断传感器读数是否为最大距离读数，如果是则舍弃，否则进行5~8行运算——通过将一个正态分布和一个均匀分布混合得到似然结果，注意该算法第8行中的$z_{max}$并非随机测量带来的误差，而是传感器的最大测量距离$z_{max}$！（此处需要对比源码查看）故基于似然模型的算法只使用了$z_{rand}$和$z_{hit}$参数，要保证$z_{rand}+z_{hit}=1$。
以上，基于AMCL定位方法的算法和模型分析结束，从上述所有模型和算法设计到的参数来看，需要重点调试的是AMCL中撒点粒子数、有效粒子数、里程计采样算法中的四个$\alpha$参数、似然域模型中的误差参数$z_{hit}$和$z_{rand}$、波束模型的四个误差参数以及最大测量距离$z_{max}$.

博主有两年多ROS的使用经验，目前仍在不停研究中。本系列ROS及SLAM进阶教程将涵盖ROS的进阶功能使用、机器人SLAM及导航的设计及研究等领域，持续不断更新中。如果大家有相关问题或发现作者漏洞欢迎私戳，同时欢迎关注收藏。
同时欢迎关注博主Git：
https://github.com/redglassli