手写机器学习算法系列06——DBSCAN

引言

我们在上一节手写机器学习算法系列05——k-means介绍了K-means聚类算法和其python实现。但是世界上没有完美的算法，k-means也存在着诸如不适用于非凸样本，超参数簇聚数目不好指定且对结果影响极大等缺点，例如：

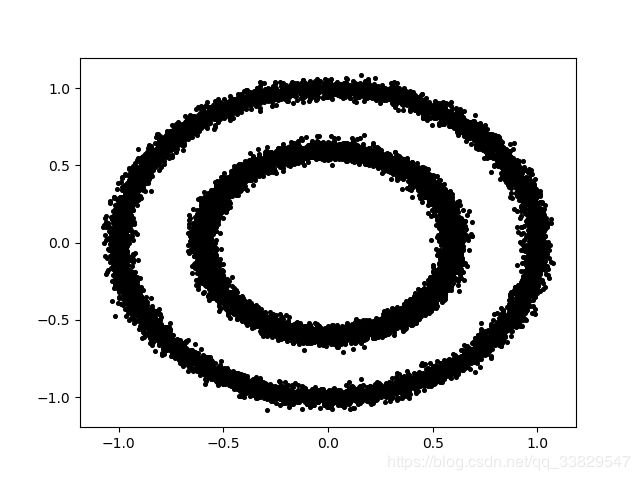
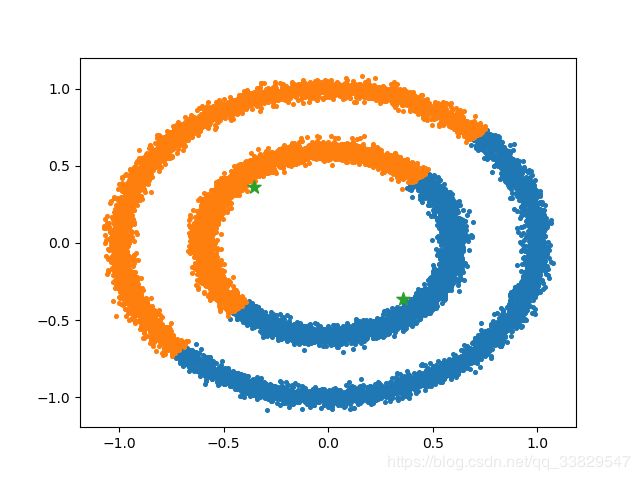
这个样本集我们可以看出有2个簇聚，分别是外面的圆和内部的圆，但是使用k-means来进行聚类，得出的效果可能是这样：

这就不符合我们预期的结果。至于超参数簇聚数目难以指定就更好理解了，千万级别的样本集根本就不知道应该会有几个簇，只能玄学调参慢慢试。

针对k-means的上述缺点，今天带来另一种聚类算法，基于密度的聚类算法——DBSCAN。

DBSCAN算法原理

首先我们要明确几个概念：

• $ϵ$-邻域：以某个样本点为圆心，以$ϵ$为半径画圆，圆的区域就叫这个样本点的$ϵ$-领域

• 核心对象：如果某个样本点的$ϵ$-邻域存在至少min_pts个样本点，那么这个样本点被称为核心对象。

• 直接密度可达：如果样本点p是核心对象，且样本点q存在于样本点p的$ϵ$-邻域内，那么我们说样本点p到样本点q是直接密度可达的。直接密度可达关系不具有对称性，也不具有传递性。

• 密度可达：如果有样本点$p_1、p_2、p_3...p_n$，满足$p_{i-1}$到$p_i$是直接密度可达的，那么我们说$p_1$到$p_n$是密度可达的。密度可达具有传递性，但不具有对称性。

• 密度相连：如果从核心点$p$出发到$q_1$和$q_2$都是密度可达的，那么我们说$q_1$和$q_2$是密度相连的。密度相连具有对称性，也具有传递性。

• 簇聚：如果样本点$p_1、p_2、p_3...p_n$之间互相都是密度相连的，那么我们说这些样本点属于同一个簇聚。

• 边缘对象：如果样本点$p$属于某一个簇聚，但不属于核心对象，则称边缘对象。

• 噪声点：如果从任何一样本点出发到样本点$p$，都不是密度可达，那么我们说$p$是噪声点，或者叫离群点。

如下图所示：

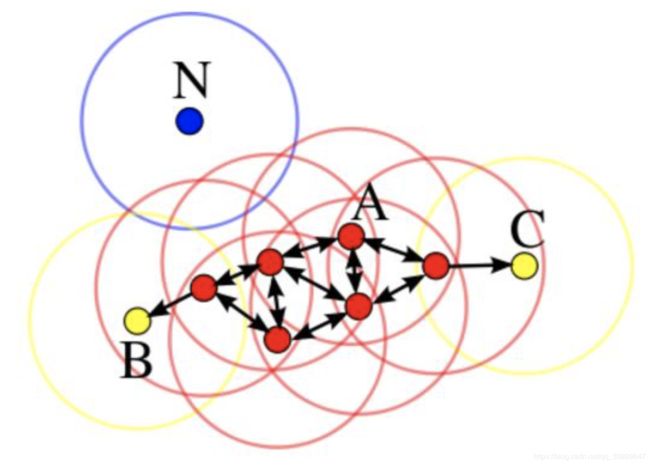
上图设定的min_pts为3，红色的点是核心对象；黄色的点是边缘对象；箭头代表了直接密度可达关系；红色和黄色的点集两两满足密度相连关系，即属于同一个簇；蓝色的点是噪声点。

DBSCAN聚类算法就是通过输入样本集D、邻域半径-$ϵ$和密度阈值min_pts，将相互之间密度相连的样本点聚成簇。算法伪代码如下：

手写DBSCAN算法

样本点存在是否访问的状态量，因此我们构建一个Point对象，包含访问状态和样本点数据两个属性：

class Point:
    def __init__(self,data):
        self.visited = False
        self.data = data

然后实现DBSCAN聚类的核心算法：

import numpy as np 
from point import Point

class DBSCANCluster:
    
    def __init__(self,ndarray,epsilon,min_pts):
        self.epsilon = epsilon # 邻域半径
        self.min_pts = min_pts # 密度阈值
        self.datas = []  # 样本集
        for item in ndarray:
            self.datas.append(Point(item)) # 将ndarray装配到Point对象中然后放入list

    
    def cluster(self):
        ''' 聚类
        '''       
        result=[] # 簇聚结果
        noise =[] # 噪声点集
        while True:
            P = self.__pick() # 选取一个未被访问的对象
            if P == None: # 如果没有未访问的样本点
                return result,noise  # 返回结果
                
			# 获得P点邻域的所以对象数量和未被访问的对象list
            num,N = self.__pts_scan(P)  
            if num >= self.min_pts: # 如果是核心对象（邻域样本数大于密度阈值）
                new_cluster=[] # 构建一个新簇
                new_cluster.append(P.data) # 将P点加入新簇
                for p in N: # 遍历核心对象P邻域内的样本集
                    new_cluster.append(p.data) # 样本加入新簇
                    num,pts = self.__pts_scan(p) # 获得样本的邻域点数和未被访问的对象list
                    if num >= self.min_pts: # 如果样本是核心对象
                        N += pts # 则将其邻域内的未访问样本加入迭代样本集
                result.append(new_cluster) # 迭代终止后将新簇加入簇聚结果
            else: # 如果P不是核心对象
                noise.append(P.data) # 加入噪声点集


   
    def __pick(self):
        ''' 选择一个未被访问的样本点
        '''
        for index in range(len(self.datas)):
            if self.datas[index].visited == False:
                self.datas[index].visited = True
                return self.datas[index]
        
        return None

    def __pts_scan(self,pts):
        ''' 扫描某样本点epsilon-邻域内的所有点
        '''
        result = []
        num = 0
        for index in range(len(self.datas)):
            if self.__distance(pts.data,self.datas[index].data) <= self.epsilon:
                num += 1
                if self.datas[index].visited == False:
                    self.datas[index].visited = True
                    result.append(self.datas[index])
                    
        return num,result

    def __distance(self,p1,p2):
        '''计算两点间距
        '''
        tmp=0
        for i in range(len(p1)):
            tmp += pow(p1[i]-p2[i],2)
        return pow(tmp,0.5)

算法测试

import numpy as np 
import pandas as pd
import matplotlib.pyplot as plt
from dbscan import DBSCANCluster 
from sklearn.datasets import make_circles # 数据集就直接导入sklearn中的

if __name__ == "__main__":
    datas, label= make_circles(n_samples=15000, shuffle=True, noise=0.03, random_state=None, factor=0.6)
    plt.scatter(datas[:,0],datas[:,1],c="black",s=7)
    plt.savefig('circles.png') # 保存样本集的散点图
    plt.clf()
    cluster =DBSCANCluster(datas,0.1,3)
    result,noise=cluster.cluster()
    
    for item in result:
        plt.scatter([x[0] for x in item],[x[1] for x in item],s=7)
    for item in noise:
        plt.scatter(item[0],item[1],s=7,c="black")
    plt.savefig('result_circles.png') # 保存聚类结果

输出结果：

样本集散点图

聚类结果图

总结

测试代码的运行结果符合我们的预期，但是运行时间耗费了很久，这是因为DBSCAN的时间复杂度高达$O(N^2)$。也可以使用K-D-Tree来优化数据结果，使时间复杂度降低到$O(N\log (N))$。先留个坑，以后有时间实现了再另外开篇文章。